Centrality Measures allows us to pinpoint the most important nodes of a Graph. This essentially helps us to identify :
Firstly, we need to consider the famous social graph published in 1977 called Zachary’s Karate Club graph. It is an in-built Graph in Networkx. All the centrality measures will be demonstrated using this Graph.
import matplotlib.pyplot as plt
import networkx as nx
G = nx.karate_club_graph()
plt.figure(figsize =(15, 15))
nx.draw_networkx(g, with_labels = True)
|
Output:
 Commonly used techniques for Centrality Measures are as follows :
Commonly used techniques for Centrality Measures are as follows :
Degree Centrality :
This is based on the assumption that important nodes have many connections.
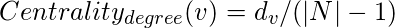
, where
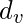
is the Degree of node v and N is the set of all nodes of the Graph.
In Networkx,
deg_centrality = nx.degree_centrality(G)
print(deg_centrality)
|
Output:
{0: 0.48484848484848486,
1: 0.2727272727272727,
2: 0.30303030303030304,
3: 0.18181818181818182,
4: 0.09090909090909091,
5: 0.12121212121212122,
6: 0.12121212121212122,
7: 0.12121212121212122,
8: 0.15151515151515152,
9: 0.06060606060606061,
10: 0.09090909090909091,
11: 0.030303030303030304,
12: 0.06060606060606061,
13: 0.15151515151515152,
14: 0.06060606060606061,
15: 0.06060606060606061,
16: 0.06060606060606061,
17: 0.06060606060606061,
18: 0.06060606060606061,
19: 0.09090909090909091,
20: 0.06060606060606061,
21: 0.06060606060606061,
22: 0.06060606060606061,
23: 0.15151515151515152,
24: 0.09090909090909091,
25: 0.09090909090909091,
26: 0.06060606060606061,
27: 0.12121212121212122,
28: 0.09090909090909091,
29: 0.12121212121212122,
30: 0.12121212121212122,
31: 0.18181818181818182,
32: 0.36363636363636365,
33: 0.5151515151515151}
Returns a dictionary of size equal to the number of nodes in Graph G, where the ith element is the degree centrality measure of the ith node. For Directed Graphs, the measures are different for in degree and out degree. These are calculated by:
in_deg_centrality = nx.in_degree_centrality(G)
out_deg_centrality = nx.out_degree_centrality(G)
|
where
g is a Directed Graph.
Closeness Centrality :
This is based on the assumption that important nodes are close to other nodes. It is calculated as the sum of the path lengths from the given node to all other nodes. But for a node which cannot reach all other nodes, closeness centrality is measured using the following formula :
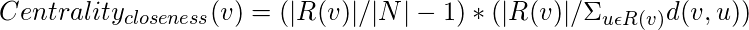
where, R(v) is the set of all nodes v can reach.
close_centrality = nx.closeness_centrality(G)
print(close_centrality)
|
Output:
{0: 0.5689655172413793,
1: 0.4852941176470588,
2: 0.559322033898305,
3: 0.4647887323943662,
4: 0.3793103448275862,
5: 0.38372093023255816,
6: 0.38372093023255816,
7: 0.44,
8: 0.515625,
9: 0.4342105263157895,
10: 0.3793103448275862,
11: 0.36666666666666664,
12: 0.3707865168539326,
13: 0.515625,
14: 0.3707865168539326,
15: 0.3707865168539326,
16: 0.28448275862068967,
17: 0.375,
18: 0.3707865168539326,
19: 0.5,
20: 0.3707865168539326,
21: 0.375,
22: 0.3707865168539326,
23: 0.39285714285714285,
24: 0.375,
25: 0.375,
26: 0.3626373626373626,
27: 0.4583333333333333,
28: 0.4520547945205479,
29: 0.38372093023255816,
30: 0.4583333333333333,
31: 0.5409836065573771,
32: 0.515625,
33: 0.55}
Betweenness Centrality :
It assumes that important nodes connect other nodes. The formula for calculating Betweenness Centrality is as follows:

where
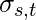
is the number of shortest paths between nodes s and t.

is the number of shortest paths between nodes s and t that pass through v.
We may or may not include node v itself for the calculation.
For Graphs with a large number of nodes, the value of betweenness centrality is very high. So, we can normalize the value by dividing with number of node pairs (excluding the current node). For Directed Graphs, the number of node pairs are
(|N|-1)*(|N|-2), while for Undirected Graphs, the number of node pairs are
(1/2)*(|N|-1)*(|N|-2).
bet_centrality = nx.betweenness_centrality(G, normalized = True,
endpoints = False)
print(bet_centrality)
|
Output:
{0: 0.43763528138528146,
1: 0.053936688311688304,
2: 0.14365680615680618,
3: 0.011909271284271283,
4: 0.0006313131313131313,
5: 0.02998737373737374,
6: 0.029987373737373736,
7: 0.0,
8: 0.05592682780182781,
9: 0.0008477633477633478,
10: 0.0006313131313131313,
11: 0.0,
12: 0.0,
13: 0.04586339586339586,
14: 0.0,
15: 0.0,
16: 0.0,
17: 0.0,
18: 0.0,
19: 0.03247504810004811,
20: 0.0,
21: 0.0,
22: 0.0,
23: 0.017613636363636363,
24: 0.0022095959595959595,
25: 0.0038404882154882154,
26: 0.0,
27: 0.02233345358345358,
28: 0.0017947330447330447,
29: 0.0029220779220779218,
30: 0.014411976911976909,
31: 0.13827561327561325,
32: 0.145247113997114,
33: 0.30407497594997596}
Page Rank :
Page Rank Algorithm was developed by Google founders to measure the importance of webpages from the hyperlink network structure. Page Rank assigns a score of importance to each node. Important nodes are those with many inlinks from important pages. It mainly works for Directed Networks.
n -> Number of nodes
k -> Number of steps
All nodes have a Page Rank of 1/n
Repeat k times :
For node u pointing to node v, add Page Rank of u
divided by out degree of u to the Page Rank of v
For understanding Page Rank, we will consider the following Graph:

Let k = 2
Initially,
A -> 1/5
B -> 1/5
C -> 1/5
D -> 1/5
E -> 1/5
After first iteration,
A -> 1/15+1/5 = 4/15
B -> 1/5+1/5 = 2/5
C -> 1/10+1/15 = 1/6
D -> 1/10
E -> 1/15
After second iteration,
A -> 1/30+1/15 = 1/10
B -> 4/15+1/6 = 13/30
C -> 1/5+1/30 = 7/30
D -> 1/5
E -> 1/30
So, after 2 iterations, Page Rank is as follows:
B > C > D > A > E
Page Rank of a node at step
k is the probability that a random walker lands on the node after taking
k steps.
Now let us consider the following network,

For a Random Walk where
k tends to infinity, it will eventually go to F or G and will get stuck there. Thus Page Rank for F = 1/2, G = 1/2, the rest nodes will have Page Rank of 0. This is solved by introducing a ‘damping parameter’
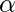
.
Each node has a Page Rank of 1/n
Start on a Random Node
Repeat k times:
With probability 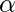 , choose an outgoing edge at random and follow it to the next node.
With probability
, choose an outgoing edge at random and follow it to the next node.
With probability  , choose a random node and go to it.
, choose a random node and go to it.
The value of alpha is usually set between 0.8 to 0.9.
pr = nx.pagerank(G, alpha = 0.8)
print(pr)
|
Output:
{0: 0.09456117898156402,
1: 0.05152334607950815,
2: 0.05510962827358582,
3: 0.03520686871052657,
4: 0.022556530085318473,
5: 0.02965434765152121,
6: 0.02965434765152121,
7: 0.02429306613631948,
8: 0.029203590410895465,
9: 0.014918270732782356,
10: 0.022556530085318473,
11: 0.010610337618460166,
12: 0.015304584795945321,
13: 0.028920243421725694,
14: 0.015180200879547068,
15: 0.015180200879547068,
16: 0.01774436545128434,
17: 0.01519007845263465,
18: 0.015180200879547068,
19: 0.019817255738040863,
20: 0.015180200879547068,
21: 0.01519007845263465,
22: 0.015180200879547068,
23: 0.03138523208020211,
24: 0.021678994504154954,
25: 0.021582293035938838,
26: 0.015815184517974507,
27: 0.02572094617382946,
28: 0.019815535386497624,
29: 0.026528036905982717,
30: 0.024432622368453834,
31: 0.03672846196415318,
32: 0.07006405452640968,
33: 0.09833298540908077}
These are the various measures of Centrality in a Network. There are other methods like Load Centrality, Katz Centrality, Percolation Centrality etc.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...