Maximum area of a Rectangle that can be circumscribed about a given Rectangle of size LxW
Last Updated :
27 Apr, 2021
Given a rectangle of dimensions L and W. The task is to find the maximum area of a rectangle that can be circumscribed about a given rectangle with dimensions L and W.
Examples:
Input: L = 10, W = 10
Output: 200
Input: L = 18, W = 12
Output: 450
Approach: Let below is the given rectangle EFGH of dimensions L and W. We have to find the area of rectangle ABCD which is circumscribing rectangle EFGH.

In the above figure:
If 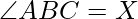 then
then 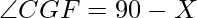 as GCF is right angled triangle.
as GCF is right angled triangle.
Therefore,

=> 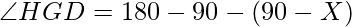
=> 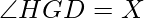
Similarly,
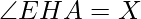
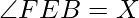
Now, The area of rectangle ABCD is given by:
Area = AB * AD
Area = (AE + EB)*(AH + HD) …..(1)
According to the projection rule:
AE = L*sin(X)
EB = W*cos(X)
AH = L*cos(X)
HD = W*sin(X)
Substituting the value of the above projections in equation (1) we have:
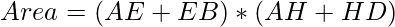
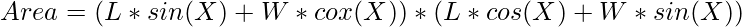
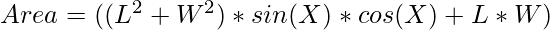
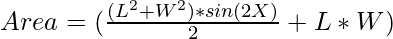
Now to maximize the area, the value of sin(2X) must be maximum i.e., 1.
Therefore after substituting sin(2X) as 1 we have,
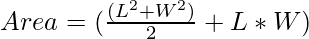
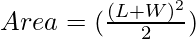
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double AreaofRectangle(int L, int W)
{
double area = (W + L) * (W + L) / 2;
return area;
}
int main()
{
int L = 18;
int W = 12;
cout << AreaofRectangle(L, W);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static double AreaofRectangle(int L, int W)
{
double area = (W + L) * (W + L) / 2;
return area;
}
public static void main(String args[])
{
int L = 18;
int W = 12;
System.out.println(AreaofRectangle(L, W));
}
}
|
Python3
def AreaofRectangle(L, W):
area =(W + L)*(W + L)/2
return area
if __name__ == "__main__":
L = 18
W = 12
print(AreaofRectangle(L, W))
|
C#
using System;
class GFG{
static double AreaofRectangle(int L, int W)
{
double area = (W + L) * (W + L) / 2;
return area;
}
public static void Main(String []args)
{
int L = 18;
int W = 12;
Console.Write(AreaofRectangle(L, W));
}
}
|
Javascript
<script>
function AreaofRectangle(L, W) {
var area = parseFloat(((W + L) * (W + L)) / 2).toFixed(1);
return area;
}
var L = 18;
var W = 12;
document.write(AreaofRectangle(L, W));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...