Mathematics | Rings, Integral domains and Fields
Last Updated :
16 Feb, 2023
Prerequisite – Mathematics | Algebraic Structure
Ring – Let addition (+) and Multiplication (.) be two binary operations defined on a non empty set R. Then R is said to form a ring w.r.t addition (+) and multiplication (.) if the following conditions are satisfied:
- (R, +) is an abelian group ( i.e commutative group)
- (R, .) is a semigroup
- For any three elements a, b, c
 R the left distributive law a.(b+c) =a.b + a.c and the right distributive property (b + c).a =b.a + c.a holds.
R the left distributive law a.(b+c) =a.b + a.c and the right distributive property (b + c).a =b.a + c.a holds.
Therefore a non- empty set R is a ring w.r.t to binary operations + and . if the following conditions are satisfied.
- For all a, b
 R, a+b
R, a+b R,
R, - For all a, b, c
 R a+(b+c)=(a+b)+c,
R a+(b+c)=(a+b)+c, - There exists an element in R, denoted by 0 such that a+0=a for all a
 R
R - For every a
 R there exists an y
R there exists an y  R such that a+y=0. y is usually denoted by -a
R such that a+y=0. y is usually denoted by -a - a+b=b+a for all a, b
 R.
R. - a.b
 R for all a, b
R for all a, b  R.
R. - a.(b.c)=(a.b).c for all a, b, c
 R
R - For any three elements a, b, c
 R a.(b+c) =a.b + a.c and (b + c).a =b.a + c.a. And the ring is denoted by (R, +, .).
R a.(b+c) =a.b + a.c and (b + c).a =b.a + c.a. And the ring is denoted by (R, +, .).
Some Examples –
- (
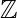 , + ) is a commutative group .(
, + ) is a commutative group .(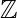 , .) is a semi-group. The distributive law also holds. So, ((
, .) is a semi-group. The distributive law also holds. So, ((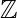 , +, .) is a ring.
, +, .) is a ring.
- Ring of Integers modulo n: For a n
 [Tex]\mathbb{N} [/Tex]let
[Tex]\mathbb{N} [/Tex]let 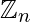 be the classes of residues of integers modulo n. i.e
be the classes of residues of integers modulo n. i.e 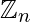 ={
={ ).
).
(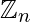 , +) is a commutative group ere + is addition(mod n).
, +) is a commutative group ere + is addition(mod n).
(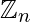 , .) is a semi group here . denotes multiplication (mod n).
, .) is a semi group here . denotes multiplication (mod n).
Also the distributive laws hold. So ((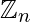 , +, .) is a ring.
, +, .) is a ring. - The set S = {0, 1, 2, 3, 4} is a ring with respect to operation addition modulo 5 & multiplication modulo 5.


(S,+5) is an Abelian Group. From the above 1st composition table we can conclude that (S,+5) satisfies –
- Closure : a ∈ S ,b ∈ S => a +5 b ∈ S ; ∀ a,b ∈ S
- Associativity : (a+5b)+5c = a+5(b+5c) ; ∀ a,b,c ∈ S.
- Existence of identity 0 : (a+5b)+5c = a+5(b+5c) ; ∀ a,b,c ∈ S.
- Existence of inverse: Inverse of 0, 1, 2, 3, 4 are 0, 4, 3, 2 , 1 respectively &
- Commutative : (a+5b) = (b+5a) ; ∀ a,b ∈ S
2. (S,*5) is an Semi Group. From the above 2nd composition table we can conclude that (S,*5) satisfies :
- Closure : a ∈ S ,b ∈ S => a *5 b ∈ S ; ∀ a,b ∈ S
- Associativity : (a*5b)*5c = a*5(b*5c) ; ∀ a,b,c ∈ S
3. Multiplication is distributive over addition :
(a) Left Distributive : ∀ a, b, c ∈ S :
a*5 (b +5 c)
= [ a * (b + c) ] mod 5
= [a*b + a*c] mod 5
= (a *5 b) +5 (a *5 c)
⇒ Multiplication modulo 5 is distributive over addition modulo 5.
Similarly , Right Distributive law can also be proved.
So, we can conclude that (S,+,*) is a Ring.
Many other examples also can be given on rings like (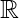 , +, .), (
, +, .), (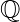 , +, .) and so on.
, +, .) and so on.
Before discussing further on rings, we define Divisor of Zero in A ringand the concept of unit.
Divisor of Zero in A ring –
In a ring R a non-zero element is said to be divisor of zero if there exists a non-zero element b in R such that a.b=0 or a non-zero element c in R such that c.a=0 In the first case a is said to be a left divisor of zero and in the later case a is said to be a right divisor of zero . Obviously if R is a commutative ring then if a is a left divisor of zero then a is a right divisor of zero also .
Example – In the ring (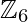 , +, .)
, +, .) 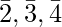 are divisors of zero since
are divisors of zero since
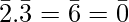 and so on .
and so on .
On the other hand the rings (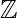 , +, .), (
, +, .), (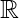 , +, .), (
, +, .), (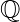 , +, .) contains no divisor of zero .
, +, .) contains no divisor of zero .
Units –
In a non trivial ring R( Ring that contains at least to elements) with unity an element a in R is said to be an unit if there exists an element b in R such that a.b=b.a=I, I being the unity in R. b is said to be multiplicative inverse of a.
Some Important results related to Ring:
- If R is a non-trivial ring(ring containing at least two elements ) withunity I then I
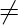 0.
0. - If I be a multiplicative identity in a ring R then I is unique .
- If a be a unit in a ring R then its multiplicative inverse is unique .
- In a non trivial ring R the zero element has no multiplicative inverse .
Types of Ring :
- Null Ring : The singleton set : {0} with 2 binary operations ‘+’ & ‘*” defined by :
0+0 = 0 & 0*0 = 0 is called zero/ null ring. - Ring with Unity : If there exists an element in R denoted by 1 such that :
1*a = a* 1 = a ; ∀ a ∈ R, then the ring is called Ring with Unity. - Commutative Ring : If the multiplication in the ring R is also commutative, then ring is called a commutative ring.
- Ring of Integers : The set I of integers with 2 binary operations ‘+’ & ‘*’ is known as ring of Integers.
- Boolean Ring : A ring whose every element is idempotent, i.e. , a2 = a ; ∀ a ∈ R
Now we introduce a new concept Integral Domain.
Integral Domain – A non -trivial ring(ring containing at least two elements) with unity is said to be an integral domain if it is commutative and contains no divisor of zero ..
Examples –
The rings (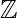 , +, .), (
, +, .), (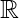 , +, .), (
, +, .), (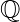 , +, .) are integral domains.
, +, .) are integral domains.
The ring (2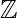 , +, .) is a commutative ring but it neither contains unity nor divisors of zero. So it is not an integral domain.
, +, .) is a commutative ring but it neither contains unity nor divisors of zero. So it is not an integral domain.
Next we will go to Field .
Field – A non-trivial ring R with unity is a field if it is commutative and each non-zero element of R is a unit . Therefore a non-empty set F forms a field .r.t two binary operations + and . if
- For all a, b
 F, a+b
F, a+b F,
F, - For all a, b, c
 F a+(b+c)=(a+b)+c,
F a+(b+c)=(a+b)+c, - There exists an element in F, denoted by 0 such that a+0=a for all a
 F
F - For every a
 R there exists an y
R there exists an y  R such that a+y=0. y is usually denoted by (-a)
R such that a+y=0. y is usually denoted by (-a) - a+b=b+a for all a, b
 F.
F. - a.b
 F for all a.b
F for all a.b  F.
F. - a.(b.c)=(a.b).c for all a, b
 F
F - There exists an element I in F, called the identity element such that a.I=a for all a in F
- For each non-zero element a in F there exists an element, denoted by
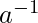 in F such that
in F such that 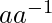 =I.
=I. - a.b =b.a for all a, b in F .
- a.(b+c) =a.b + a.c for all a, b, c in F
Examples – The rings (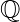 , +, .), (
, +, .), (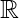 , + . .) are familiar examples of fields.
, + . .) are familiar examples of fields.
Some important results:
- A field is an integral domain.
- A finite integral domain is a field.
- A non trivial finite commutative ring containing no divisor of zero is an integral domain
Share your thoughts in the comments
Please Login to comment...