Lowest Common Ancestor in a Binary Search Tree.
Last Updated :
27 Dec, 2023
Given two values n1 and n2 in a Binary Search Tree, find the Lowest Common Ancestor (LCA). You may assume that both values exist in the tree.
Let T be a rooted tree. The lowest common ancestor between two nodes n1 and n2 is defined as the lowest node in T that has both n1 and n2 as descendants (where we allow a node to be a descendant of itself). The LCA of n1 and n2 in T is the shared ancestor of n1 and n2 that is located farthest from the root [i.e., closest to n1 and n2].
Examples:
Input Tree:
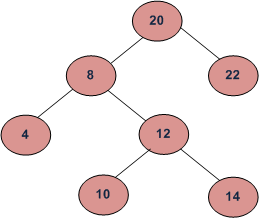
Input: LCA of 10 and 14
Output: 12
Explanation: 12 is the closest node to both 10 and 14
which is a ancestor of both the nodes.
Input: LCA of 8 and 14
Output: 8
Explanation: 8 is the closest node to both 8 and 14
which is a ancestor of both the nodes.
Lowest Common Ancestor in a Binary Search Tree using Recursion:
To solve the problem follow the below idea:
For Binary search tree, while traversing the tree from top to bottom the first node which lies in between the two numbers n1 and n2 is the LCA of the nodes, i.e. the first node n with the lowest depth which lies in between n1 and n2 (n1<=n<=n2) n1 < n2.
So just recursively traverse the BST , if node’s value is greater than both n1 and n2 then our LCA lies in the left side of the node, if it is smaller than both n1 and n2, then LCA lies on the right side. Otherwise, the root is LCA (assuming that both n1 and n2 are present in BST)
Follow the given steps to solve the problem:
- Create a recursive function that takes a node and the two values n1 and n2.
- If the value of the current node is less than both n1 and n2, then LCA lies in the right subtree. Call the recursive function for the right subtree.
- If the value of the current node is greater than both n1 and n2, then LCA lies in the left subtree. Call the recursive function for the left subtree.
- If both the above cases are false then return the current node as LCA.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node *left, *right;
};
node* lca(node* root, int n1, int n2)
{
if (root == NULL)
return NULL;
if (root->data > n1 && root->data > n2)
return lca(root->left, n1, n2);
if (root->data < n1 && root->data < n2)
return lca(root->right, n1, n2);
return root;
}
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = Node->right = NULL;
return (Node);
}
int main()
{
node* root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
int n1 = 10, n2 = 14;
node* t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
n1 = 14, n2 = 8;
t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
n1 = 10, n2 = 22;
t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left, *right;
};
struct node* lca(struct node* root, int n1, int n2)
{
if (root == NULL)
return NULL;
if (root->data > n1 && root->data > n2)
return lca(root->left, n1, n2);
if (root->data < n1 && root->data < n2)
return lca(root->right, n1, n2);
return root;
}
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
int n1 = 10, n2 = 14;
struct node* t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 14, n2 = 8;
t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 10, n2 = 22;
t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
getchar();
return 0;
}
|
Java
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
Node lca(Node node, int n1, int n2)
{
if (node == null)
return null;
if (node.data > n1 && node.data > n2)
return lca(node.left, n1, n2);
if (node.data < n1 && node.data < n2)
return lca(node.right, n1, n2);
return node;
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
int n1 = 10, n2 = 14;
Node t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 14;
n2 = 8;
t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 10;
n2 = 22;
t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def lca(root, n1, n2):
if root is None:
return None
if(root.data > n1 and root.data > n2):
return lca(root.left, n1, n2)
if(root.data < n1 and root.data < n2):
return lca(root.right, n1, n2)
return root
root = Node(20)
root.left = Node(8)
root.right = Node(22)
root.left.left = Node(4)
root.left.right = Node(12)
root.left.right.left = Node(10)
root.left.right.right = Node(14)
n1 = 10
n2 = 14
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
n1 = 14
n2 = 8
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
n1 = 10
n2 = 22
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public virtual Node lca(Node node, int n1, int n2)
{
if (node == null) {
return null;
}
if (node.data > n1 && node.data > n2) {
return lca(node.left, n1, n2);
}
if (node.data < n1 && node.data < n2) {
return lca(node.right, n1, n2);
}
return node;
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
int n1 = 10, n2 = 14;
Node t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 14;
n2 = 8;
t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 10;
n2 = 22;
t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
}
}
|
Javascript
<script>
class Node
{
constructor(item)
{
this.data=item;
this.left=this.right=null;
}
}
let root;
function lca(node,n1,n2)
{
if (node == null)
return null;
if (node.data > n1 && node.data > n2)
return lca(node.left, n1, n2);
if (node.data < n1 && node.data < n2)
return lca(node.right, n1, n2);
return node;
}
root = new Node(20);
root.left = new Node(8);
root.right = new Node(22);
root.left.left = new Node(4);
root.left.right = new Node(12);
root.left.right.left = new Node(10);
root.left.right.right = new Node(14);
let n1 = 10, n2 = 14;
let t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 + " is " +
t.data+"<br>");
n1 = 14;
n2 = 8;
t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 + " is " +
t.data+"<br>");
n1 = 10;
n2 = 22;
t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 + " is " +
t.data+"<br>");
</script>
|
OutputLCA of 10 and 14 is 12
LCA of 14 and 8 is 8
LCA of 10 and 22 is 20
Time Complexity: O(H). where H is the height of the tree.
Auxiliary Space: O(H), If recursive stack space is ignored, the space complexity of the above solution is constant.
Below is the iterative implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
int data;
node *left, *right;
};
node* lca(node* root, int n1, int n2)
{
while (root != NULL) {
if (root->data > n1 && root->data > n2)
root = root->left;
else if (root->data < n1 && root->data < n2)
root = root->right;
else
break;
}
return root;
}
node* newNode(int data)
{
node* Node = new node();
Node->data = data;
Node->left = Node->right = NULL;
return (Node);
}
int main()
{
node* root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
int n1 = 10, n2 = 14;
node* t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
n1 = 14, n2 = 8;
t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
n1 = 10, n2 = 22;
t = lca(root, n1, n2);
cout << "LCA of " << n1 << " and " << n2 << " is "
<< t->data << endl;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left, *right;
};
struct node* lca(struct node* root, int n1, int n2)
{
while (root != NULL) {
if (root->data > n1 && root->data > n2)
root = root->left;
else if (root->data < n1 && root->data < n2)
root = root->right;
else
break;
}
return root;
}
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(20);
root->left = newNode(8);
root->right = newNode(22);
root->left->left = newNode(4);
root->left->right = newNode(12);
root->left->right->left = newNode(10);
root->left->right->right = newNode(14);
int n1 = 10, n2 = 14;
struct node* t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 14, n2 = 8;
t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
n1 = 10, n2 = 22;
t = lca(root, n1, n2);
printf("LCA of %d and %d is %d \n", n1, n2, t->data);
getchar();
return 0;
}
|
Java
class Node {
int data;
Node left, right;
Node(int item)
{
data = item;
left = right = null;
}
}
class BinaryTree {
Node root;
static Node lca(Node root, int n1, int n2)
{
while (root != null) {
if (root.data > n1 && root.data > n2)
root = root.left;
else if (root.data < n1 && root.data < n2)
root = root.right;
else
break;
}
return root;
}
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
int n1 = 10, n2 = 14;
Node t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 14;
n2 = 8;
t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 10;
n2 = 22;
t = tree.lca(tree.root, n1, n2);
System.out.println("LCA of " + n1 + " and " + n2
+ " is " + t.data);
}
}
|
Python3
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def lca(root, n1, n2):
while root:
if root.data > n1 and root.data > n2:
root = root.left
elif root.data < n1 and root.data < n2:
root = root.right
else:
break
return root
if __name__ == '__main__':
root = Node(20)
root.left = Node(8)
root.right = Node(22)
root.left.left = Node(4)
root.left.right = Node(12)
root.left.right.left = Node(10)
root.left.right.right = Node(14)
n1 = 10
n2 = 14
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
n1 = 14
n2 = 8
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
n1 = 10
n2 = 22
t = lca(root, n1, n2)
print("LCA of %d and %d is %d" % (n1, n2, t.data))
|
C#
using System;
public class Node {
public int data;
public Node left, right;
public Node(int item)
{
data = item;
left = right = null;
}
}
public class BinaryTree {
public Node root;
public virtual Node lca(Node root, int n1, int n2)
{
while (root != null) {
if (root.data > n1 && root.data > n2)
root = root.left;
else if (root.data < n1 && root.data < n2)
root = root.right;
else
break;
}
return root;
}
public static void Main(string[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(20);
tree.root.left = new Node(8);
tree.root.right = new Node(22);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(12);
tree.root.left.right.left = new Node(10);
tree.root.left.right.right = new Node(14);
int n1 = 10, n2 = 14;
Node t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 14;
n2 = 8;
t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
n1 = 10;
n2 = 22;
t = tree.lca(tree.root, n1, n2);
Console.WriteLine("LCA of " + n1 + " and " + n2
+ " is " + t.data);
}
}
|
Javascript
<script>
class Node
{
constructor(item)
{
this.data = item;
this.left = null;
this.right = null;
}
}
var root = null;
function lca(root, n1, n2)
{
while (root != null)
{
if (root.data > n1 && root.data > n2)
root = root.left;
else if (root.data < n1 && root.data < n2)
root = root.right;
else break;
}
return root;
}
root = new Node(20);
root.left = new Node(8);
root.right = new Node(22);
root.left.left = new Node(4);
root.left.right = new Node(12);
root.left.right.left = new Node(10);
root.left.right.right = new Node(14);
var n1 = 10, n2 = 14;
var t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 +
" is " + t.data + "<br>");
n1 = 14;
n2 = 8;
t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 +
" is " + t.data+ "<br>");
n1 = 10;
n2 = 22;
t = lca(root, n1, n2);
document.write("LCA of " + n1 + " and " + n2 +
" is " + t.data+ "<br>");
</script>
|
OutputLCA of 10 and 14 is 12
LCA of 14 and 8 is 8
LCA of 10 and 22 is 20
Time Complexity: O(H). where H is the height of the tree
Auxiliary Space: O(1). The space complexity of the above solution is constant.
Lowest Common Ancestor in a Binary Search Tree using Morris traversal:

Follow the steps to implement the above approach:
- Initialize a pointer curr to the root of the tree.
- While curr is not NULL, do the following:
- If curr has no left child, check if curr is either of the two nodes we are interested in. If it is, return curr. Otherwise, move curr to its right child.
- If curr has a left child, find the inorder predecessor pre of curr by moving to the rightmost node in the left subtree of curr.
- If the right child of pre is NULL, set it to curr and move curr to its left child.
- If the right child of pre is curr, set it to NULL and restore the original tree structure. Then check if curr is either of the two nodes we are interested in. If it is, return curr. Otherwise, move curr to its right child.
- If the two nodes we are interested in are not found during the traversal, return NULL
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
struct TreeNode {
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL || root == p || root == q) {
return root;
}
TreeNode* leftLCA = lowestCommonAncestor(root->left, p, q);
TreeNode* rightLCA = lowestCommonAncestor(root->right, p, q);
if (leftLCA != NULL && rightLCA != NULL) {
return root;
}
return (leftLCA != NULL) ? leftLCA : rightLCA;
}
int main() {
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(4);
root->left->right = new TreeNode(3);
root->right = new TreeNode(6);
root->right->right = new TreeNode(7);
root->right->right->right = new TreeNode(8);
TreeNode* p = root->left;
TreeNode* q = root->left->right;
TreeNode* lca1 = lowestCommonAncestor(root, p, q);
cout << "LCA of " << p->val << " and " << q->val << " is " << lca1->val << endl;
TreeNode* x = root->right->right;
TreeNode* y = root->right->right->right;
TreeNode* lca2 = lowestCommonAncestor(root, x, y);
cout << "LCA of " << x->val << " and " << y->val << " is " << lca2->val << endl;
return 0;
}
|
Java
class TreeNode {
int val;
TreeNode left, right;
public TreeNode(int x) {
val = x;
left = right = null;
}
}
public class LowestCommonAncestor {
public static TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode leftLCA = lowestCommonAncestor(root.left, p, q);
TreeNode rightLCA = lowestCommonAncestor(root.right, p, q);
if (leftLCA != null && rightLCA != null) {
return root;
}
return (leftLCA != null) ? leftLCA : rightLCA;
}
public static void main(String[] args) {
TreeNode root = new TreeNode(5);
root.left = new TreeNode(4);
root.left.right = new TreeNode(3);
root.right = new TreeNode(6);
root.right.right = new TreeNode(7);
root.right.right.right = new TreeNode(8);
TreeNode p = root.left;
TreeNode q = root.left.right;
TreeNode lca1 = lowestCommonAncestor(root, p, q);
System.out.println("LCA of " + p.val + " and " + q.val + " is " + lca1.val);
TreeNode x = root.right.right;
TreeNode y = root.right.right.right;
TreeNode lca2 = lowestCommonAncestor(root, x, y);
System.out.println("LCA of " + x.val + " and " + y.val + " is " + lca2.val);
}
}
|
Python3
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def lowest_common_ancestor(root, p, q):
if not root or root == p or root == q:
return root
left_lca = lowest_common_ancestor(root.left, p, q)
right_lca = lowest_common_ancestor(root.right, p, q)
if left_lca and right_lca:
return root
return left_lca if left_lca else right_lca
root = TreeNode(5)
root.left = TreeNode(4)
root.left.right = TreeNode(3)
root.right = TreeNode(6)
root.right.right = TreeNode(7)
root.right.right.right = TreeNode(8)
p = root.left
q = root.left.right
lca1 = lowest_common_ancestor(root, p, q)
print(f"LCA of {p.val} and {q.val} is {lca1.val}")
x = root.right.right
y = root.right.right.right
lca2 = lowest_common_ancestor(root, x, y)
print(f"LCA of {x.val} and {y.val} is {lca2.val}")
|
C#
using System;
public class TreeNode
{
public int val;
public TreeNode left, right;
public TreeNode(int x)
{
val = x;
left = right = null;
}
}
public class BinaryTree
{
public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
{
if (root == null || root == p || root == q)
{
return root;
}
TreeNode leftLCA = LowestCommonAncestor(root.left, p, q);
TreeNode rightLCA = LowestCommonAncestor(root.right, p, q);
if (leftLCA != null && rightLCA != null)
{
return root;
}
return leftLCA != null ? leftLCA : rightLCA;
}
public static void Main()
{
TreeNode root = new TreeNode(5);
root.left = new TreeNode(4);
root.left.right = new TreeNode(3);
root.right = new TreeNode(6);
root.right.right = new TreeNode(7);
root.right.right.right = new TreeNode(8);
TreeNode p = root.left;
TreeNode q = root.left.right;
BinaryTree binaryTree = new BinaryTree();
TreeNode lca1 = binaryTree.LowestCommonAncestor(root, p, q);
Console.WriteLine($"LCA of {p.val} and {q.val} is {lca1.val}");
TreeNode x = root.right.right;
TreeNode y = root.right.right.right;
TreeNode lca2 = binaryTree.LowestCommonAncestor(root, x, y);
Console.WriteLine($"LCA of {x.val} and {y.val} is {lca2.val}");
}
}
|
Javascript
class TreeNode {
constructor(x) {
this.val = x;
this.left = null;
this.right = null;
}
}
class BinaryTree {
lowestCommonAncestor(root, p, q) {
if (!root || root === p || root === q) {
return root;
}
const leftLCA = this.lowestCommonAncestor(root.left, p, q);
const rightLCA = this.lowestCommonAncestor(root.right, p, q);
if (leftLCA && rightLCA) {
return root;
}
return leftLCA || rightLCA;
}
}
const root = new TreeNode(5);
root.left = new TreeNode(4);
root.left.right = new TreeNode(3);
root.right = new TreeNode(6);
root.right.right = new TreeNode(7);
root.right.right.right = new TreeNode(8);
const binaryTree = new BinaryTree();
const p = root.left;
const q = root.left.right;
const lca1 = binaryTree.lowestCommonAncestor(root, p, q);
console.log(`LCA of ${p.val} and ${q.val} is ${lca1.val}`);
const x = root.right.right;
const y = root.right.right.right;
const lca2 = binaryTree.lowestCommonAncestor(root, x, y);
console.log(`LCA of ${x.val} and ${y.val} is ${lca2.val}`);
|
Output LCA of 4 and 3 is 4
LCA of 7 and 8 is 7
Time Complexity: O(N) , The time complexity of the Morris Traversal approach to find the lowest common ancestor of two nodes in a binary search tree is O(N), where N is the number of nodes in the tree.
Auxiliary Space: O(1) , The space complexity of the Morris Traversal approach is O(1), which is constant extra space.
Related Articles: Lowest Common Ancestor in a Binary Tree, LCA using Parent Pointer, Find LCA in Binary Tree using RMQ
Share your thoughts in the comments
Please Login to comment...