K’th Largest Element in BST when modification to BST is not allowed
Last Updated :
29 Oct, 2023
Given a Binary Search Tree (BST) and a positive integer k, find the k’th largest element in the Binary Search Tree.
For example, in the following BST, if k = 3, then output should be 14, and if k = 5, then output should be 10.
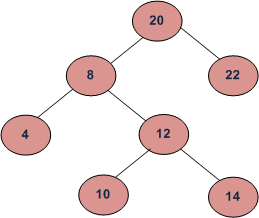
We have discussed two methods in this post. The method 1 requires O(n) time. The method 2 takes O(h) time where h is height of BST, but requires augmenting the BST (storing count of nodes in left subtree with every node).
Can we find k’th largest element in better than O(n) time and no augmentation?
Approach:
- The idea is to do reverse inorder traversal of BST. Keep a count of nodes visited.
- The reverse inorder traversal traverses all nodes in decreasing order, i.e, visit the right node then centre then left and continue traversing the nodes recursively.
- While doing the traversal, keep track of the count of nodes visited so far.
- When the count becomes equal to k, stop the traversal and print the key.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
struct Node
{
int key;
Node *left, *right;
};
Node *newNode(int item)
{
Node *temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void kthLargestUtil(Node *root, int k, int &c)
{
if (root == NULL || c >= k)
return;
kthLargestUtil(root->right, k, c);
c++;
if (c == k)
{
cout << "K'th largest element is "
<< root->key << endl;
return;
}
kthLargestUtil(root->left, k, c);
}
void kthLargest(Node *root, int k)
{
int c = 0;
kthLargestUtil(root, k, c);
}
Node* insert(Node* node, int key)
{
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
return node;
}
int main()
{
Node *root = NULL;
root = insert(root, 50);
insert(root, 30);
insert(root, 20);
insert(root, 40);
insert(root, 70);
insert(root, 60);
insert(root, 80);
int c = 0;
for (int k=1; k<=7; k++)
kthLargest(root, k);
return 0;
}
|
Java
class Node {
int data;
Node left, right;
Node(int d)
{
data = d;
left = right = null;
}
}
class BinarySearchTree {
Node root;
BinarySearchTree()
{
root = null;
}
public void insert(int data)
{
this.root = this.insertRec(this.root, data);
}
Node insertRec(Node node, int data)
{
if (node == null) {
this.root = new Node(data);
return this.root;
}
if (data == node.data) {
return node;
}
if (data < node.data) {
node.left = this.insertRec(node.left, data);
} else {
node.right = this.insertRec(node.right, data);
}
return node;
}
public class count {
int c = 0;
}
void kthLargestUtil(Node node, int k, count C)
{
if (node == null || C.c >= k)
return;
this.kthLargestUtil(node.right, k, C);
C.c++;
if (C.c == k) {
System.out.println(k + "th largest element is " +
node.data);
return;
}
this.kthLargestUtil(node.left, k, C);
}
void kthLargest(int k)
{
count c = new count();
this.kthLargestUtil(this.root, k, c);
}
public static void main(String[] args)
{
BinarySearchTree tree = new BinarySearchTree();
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
for (int i = 1; i <= 7; i++) {
tree.kthLargest(i);
}
}
}
|
Python3
class Node:
def __init__(self, data):
self.key = data
self.left = None
self.right = None
def kthLargestUtil(root, k, c):
if root == None or c[0] >= k:
return
kthLargestUtil(root.right, k, c)
c[0] += 1
if c[0] == k:
print("K'th largest element is",
root.key)
return
kthLargestUtil(root.left, k, c)
def kthLargest(root, k):
c = [0]
kthLargestUtil(root, k, c)
def insert(node, key):
if node == None:
return Node(key)
if key < node.key:
node.left = insert(node.left, key)
elif key > node.key:
node.right = insert(node.right, key)
return node
if __name__ == '__main__':
root = None
root = insert(root, 50)
insert(root, 30)
insert(root, 20)
insert(root, 40)
insert(root, 70)
insert(root, 60)
insert(root, 80)
for k in range(1,8):
kthLargest(root, k)
|
C#
using System;
public class Node
{
public int data;
public Node left, right;
public Node(int d)
{
data = d;
left = right = null;
}
}
public class BinarySearchTree
{
public Node root;
public BinarySearchTree()
{
root = null;
}
public virtual void insert(int data)
{
this.root = this.insertRec(this.root, data);
}
public virtual Node insertRec(Node node, int data)
{
if (node == null)
{
this.root = new Node(data);
return this.root;
}
if (data == node.data)
{
return node;
}
if (data < node.data)
{
node.left = this.insertRec(node.left, data);
}
else
{
node.right = this.insertRec(node.right, data);
}
return node;
}
public class count
{
private readonly BinarySearchTree outerInstance;
public count(BinarySearchTree outerInstance)
{
this.outerInstance = outerInstance;
}
internal int c = 0;
}
public virtual void kthLargestUtil(Node node, int k, count C)
{
if (node == null || C.c >= k)
{
return;
}
this.kthLargestUtil(node.right, k, C);
C.c++;
if (C.c == k)
{
Console.WriteLine(k + "th largest element is " + node.data);
return;
}
this.kthLargestUtil(node.left, k, C);
}
public virtual void kthLargest(int k)
{
count c = new count(this);
this.kthLargestUtil(this.root, k, c);
}
public static void Main(string[] args)
{
BinarySearchTree tree = new BinarySearchTree();
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
for (int i = 1; i <= 7; i++)
{
tree.kthLargest(i);
}
}
}
|
Javascript
<script>
class Node {
constructor(d)
{
this.data = d;
this.left = this.right = null;
}
}
var root = null;
function insert(data)
{
this.root = this.insertRec(this.root, data);
}
function insertRec( node , data)
{
if (node == null) {
this.root = new Node(data);
return this.root;
}
if (data == node.data) {
return node;
}
if (data < node.data) {
node.left = this.insertRec(node.left, data);
} else {
node.right = this.insertRec(node.right, data);
}
return node;
}
class count {
constructor(){this.c = 0;}
}
function kthLargestUtil( node , k, C)
{
if (node == null || C.c >= k)
return;
this.kthLargestUtil(node.right, k, C);
C.c++;
if (C.c == k) {
document.write(k + "th largest element is " +
node.data+"<br/>");
return;
}
this.kthLargestUtil(node.left, k, C);
}
function kthLargest(k)
{
c = new count();
this.kthLargestUtil(this.root, k, c);
}
insert(50);
insert(30);
insert(20);
insert(40);
insert(70);
insert(60);
insert(80);
for (i = 1; i <= 7; i++) {
kthLargest(i);
}
</script>
|
Output
K'th largest element is 80
K'th largest element is 70
K'th largest element is 60
K'th largest element is 50
K'th largest element is 40
K'th largest element is 30
K'th largest element is 20
Complexity Analysis:
- Time Complexity: O(n).
In worst case the code can traverse each and every node of the tree if the k given is equal to n (total number of nodes in the tree). Therefore overall time complexity is O(n).
- Auxiliary Space: O(h).
Max recursion stack of height h at a given time.
This article is contributed by Chirag Sharma.
Approach 2:- Iterative approach
The idea is to do reverse inorder traversal of BST. Keep a count of nodes visited.
The reverse inorder traversal traverses all nodes in decreasing order, i.e, visit the right node then centre then left and continue traversing the nodes recursively.
While doing the traversal, keep track of the count of nodes visited so far.
When the count becomes equal to k, stop the traversal and print the key.
Time Complexity : – O(N)
C++
#include <iostream>
#include <stack>
using namespace std;
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
int kthLargest(TreeNode* root, int k) {
stack<TreeNode*> st;
TreeNode* curr = root;
int count = 0;
while (curr != NULL || !st.empty()) {
while (curr != NULL) {
st.push(curr);
curr = curr->right;
}
curr = st.top();
st.pop();
count++;
if (count == k) {
return curr->val;
}
curr = curr->left;
}
return -1;
}
int main() {
TreeNode* root = new TreeNode(5);
root->left = new TreeNode(3);
root->right = new TreeNode(7);
root->left->left = new TreeNode(2);
root->left->right = new TreeNode(4);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(8);
int k = 3;
int kth_largest = kthLargest(root, k);
if (kth_largest != -1) {
cout << "The " << k << "th largest element is: " << kth_largest << endl;
} else {
cout << "The " << k << "th largest element does not exist" << endl;
}
return 0;
}
|
Java
import java.util.Stack;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int x) {
val = x;
left = null;
right = null;
}
}
class KthLargestElementBST {
public static int kthLargest(TreeNode root, int k) {
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
int count = 0;
while (curr != null || !stack.empty()) {
while (curr != null) {
stack.push(curr);
curr = curr.right;
}
curr = stack.pop();
count++;
if (count == k) {
return curr.val;
}
curr = curr.left;
}
return -1;
}
public static void main(String[] args) {
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(7);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(8);
int k = 3;
int kth_largest = kthLargest(root, k);
if (kth_largest != -1) {
System.out.println("The " + k + "th largest element is: " + kth_largest);
} else {
System.out.println("The " + k + "th largest element does not exist");
}
}
}
|
Python3
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def kthLargest(root: TreeNode, k: int) -> int:
st = []
curr = root
count = 0
while curr or st:
while curr:
st.append(curr)
curr = curr.right
curr = st.pop()
count += 1
if count == k:
return curr.val
curr = curr.left
return -1
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(7)
root.left.left = TreeNode(2)
root.left.right = TreeNode(4)
root.right.left = TreeNode(6)
root.right.right = TreeNode(8)
k = 3
kth_largest = kthLargest(root, k)
if kth_largest != -1:
print(f"The {k}th largest element is: {kth_largest}")
else:
print(f"The {k}th largest element does not exist")
|
C#
using System;
using System.Collections.Generic;
public class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x)
{
val = x;
left = null;
right = null;
}
}
public class KthLargestElementBST {
public static int KthLargest(TreeNode root, int k)
{
Stack<TreeNode> stack = new Stack<TreeNode>();
TreeNode curr = root;
int count = 0;
while (curr != null || stack.Count > 0) {
while (curr != null) {
stack.Push(curr);
curr = curr.right;
}
curr = stack.Pop();
count++;
if (count == k) {
return curr.val;
}
curr = curr.left;
}
return -1;
}
public static void Main()
{
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(7);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(8);
int k = 3;
int kth_largest = KthLargest(root, k);
if (kth_largest != -1) {
Console.WriteLine("The " + k
+ "th largest element is: "
+ kth_largest);
}
else {
Console.WriteLine(
"The " + k
+ "th largest element does not exist");
}
}
}
|
Javascript
class TreeNode {
constructor(x) {
this.val = x;
this.left = null;
this.right = null;
}
}
function kthLargest(root, k) {
const st = [];
let curr = root;
let count = 0;
while (curr || st.length) {
while (curr) {
st.push(curr);
curr = curr.right;
}
curr = st.pop();
count++;
if (count === k) {
return curr.val;
}
curr = curr.left;
}
return -1;
}
const root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(7);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(8);
const k = 3;
const kth_largest = kthLargest(root, k);
if (kth_largest !== -1) {
console.log(`The ${k}th largest element is: ${kth_largest}`);
} else {
console.log(`The ${k}th largest element does not exist`);
}
|
Output
The 3th largest element is: 6
Time complexity –The time complexity of the kthLargest function is O(h + k), where h is the height of the binary search tree and k is the given value for finding the kth largest element. This is because in the worst case, the function will need to traverse the height of the tree and then traverse k elements to find the kth largest element.
Space complexity –The space complexity of the kthLargest function is O(h), where h is the height of the binary search tree. This is because the function uses a stack to store the nodes in the right subtree, which can have at most h nodes if the tree is skewed.
Using a Max Heap:
Follow the steps to implement the above approach:
- Create an empty max heap of integers using the C++ STL priority_queue container.
- Traverse the binary search tree in reverse in-order sequence using a stack.
- At each node, add the node value to the max heap.
- If the size of the max heap becomes greater than K, remove the maximum element from the max heap.
- After we finish traversing the binary search tree, the maximum element in the max heap will be the Kth largest element in the binary search tree.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
Node *left, *right;
Node(int val)
{
data = val;
left = right = NULL;
}
};
int kthLargest(Node* root, int K)
{
priority_queue<int> maxHeap;
stack<Node*> s;
Node* curr = root;
while (curr != NULL || s.empty() == false) {
while (curr != NULL) {
s.push(curr);
curr = curr->right;
}
curr = s.top();
s.pop();
maxHeap.push(curr->data);
curr = curr->left;
}
for (int i = 1; i < K; i++) {
maxHeap.pop();
}
return maxHeap.top();
}
int main()
{
Node* root = new Node(4);
root->left = new Node(2);
root->right = new Node(9);
root->right->left = new Node(7);
root->right->right = new Node(10);
int K = 2;
int kthLargestElement = kthLargest(root, K);
cout << "The " << K
<< "th largest element in the binary search tree "
"is: "
<< kthLargestElement << endl;
return 0;
}
|
Java
import java.util.PriorityQueue;
import java.util.Stack;
class Node {
int data;
Node left, right;
Node(int val) {
data = val;
left = right = null;
}
}
public class KthLargestElement {
public static int kthLargest(Node root, int K) {
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
Stack<Node> stack = new Stack<>();
Node curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.right;
}
curr = stack.pop();
maxHeap.add(curr.data);
curr = curr.left;
}
for (int i = 1; i < K; i++) {
maxHeap.poll();
}
return maxHeap.peek();
}
public static void main(String[] args) {
Node root = new Node(4);
root.left = new Node(2);
root.right = new Node(9);
root.right.left = new Node(7);
root.right.right = new Node(10);
int K = 2;
int kthLargestElement = kthLargest(root, K);
System.out.println("The " + K + "th largest element in the binary search tree is: " + kthLargestElement);
}
}
|
Python3
import heapq
class Node:
def __init__(self, val):
self.data = val
self.left = None
self.right = None
def kthLargest(root, K):
maxHeap = []
stack = []
curr = root
while curr or stack:
while curr:
stack.append(curr)
curr = curr.right
curr = stack.pop()
heapq.heappush(maxHeap, -curr.data)
curr = curr.left
for i in range(K - 1):
heapq.heappop(maxHeap)
return -maxHeap[0]
if __name__ == '__main__':
root = Node(4)
root.left = Node(2)
root.right = Node(9)
root.right.left = Node(7)
root.right.right = Node(10)
K = 2
kthLargestElement = kthLargest(root, K)
print(f"The {K}th largest element in the binary search tree is: {kthLargestElement}")
|
C#
using System;
using System.Collections.Generic;
class Node
{
public int Data;
public Node Left, Right;
public Node(int val)
{
Data = val;
Left = Right = null;
}
}
class GFG
{
static int KthLargest(Node root, int K)
{
List<int> maxHeap = new List<int>();
Stack<Node> stack = new Stack<Node>();
Node curr = root;
while (curr != null || stack.Count > 0)
{
while (curr != null)
{
stack.Push(curr);
curr = curr.Right;
}
curr = stack.Pop();
maxHeap.Add(curr.Data);
curr = curr.Left;
}
maxHeap.Sort((x, y) => y.CompareTo(x));
return maxHeap[K - 1];
}
static void Main(string[] args)
{
Node root = new Node(4);
root.Left = new Node(2);
root.Right = new Node(9);
root.Right.Left = new Node(7);
root.Right.Right = new Node(10);
int K = 2;
int kthLargestElement = KthLargest(root, K);
Console.WriteLine("The " + K + "th largest element in the binary search tree is: " + kthLargestElement);
}
}
|
Javascript
class Node {
constructor(val) {
this.data = val;
this.left = null;
this.right = null;
}
}
function kthLargest(root, K) {
const maxHeap = new MaxHeap();
const stack = [];
let curr = root;
while (curr !== null || stack.length > 0) {
while (curr !== null) {
stack.push(curr);
curr = curr.right;
}
curr = stack.pop();
maxHeap.push(curr.data);
curr = curr.left;
}
for (let i = 1; i < K; i++) {
maxHeap.pop();
}
return maxHeap.top();
}
class MaxHeap {
constructor() {
this.heap = [];
}
push(val) {
this.heap.push(val);
this.heapifyUp(this.heap.length - 1);
}
pop() {
if (this.heap.length === 0) {
return null;
}
if (this.heap.length === 1) {
return this.heap.pop();
}
const root = this.heap[0];
this.heap[0] = this.heap.pop();
this.heapifyDown(0);
return root;
}
top() {
if (this.heap.length === 0) {
return null;
}
return this.heap[0];
}
heapifyUp(index) {
while (index > 0) {
const parentIndex = Math.floor((index - 1) / 2);
if (this.heap[index] <= this.heap[parentIndex]) {
break;
}
[this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]];
index = parentIndex;
}
}
heapifyDown(index) {
while (true) {
const leftChildIndex = 2 * index + 1;
const rightChildIndex = 2 * index + 2;
let largestIndex = index;
if (leftChildIndex < this.heap.length && this.heap[leftChildIndex] >
this.heap[largestIndex]) {
largestIndex = leftChildIndex;
}
if (rightChildIndex < this.heap.length && this.heap[rightChildIndex] >
this.heap[largestIndex]) {
largestIndex = rightChildIndex;
}
if (largestIndex === index) {
break;
}
[this.heap[index], this.heap[largestIndex]] =
[this.heap[largestIndex], this.heap[index]];
index = largestIndex;
}
}
}
const root = new Node(4);
root.left = new Node(2);
root.right = new Node(9);
root.right.left = new Node(7);
root.right.right = new Node(10);
const K = 2;
const kthLargestElement = kthLargest(root, K);
console.log(`The ${K}th largest element in the binary search tree is: ${kthLargestElement}`);
|
Output
The 2th largest element in the binary search tree is: 9
Time Complexity: O(n logk) , The worst-case time complexity of building a max heap of size k is O(klogk).
The worst-case time complexity of traversing a binary search tree in reverse in-order sequence is O(n), where n is the number of nodes in the binary search tree.
Space Complexity: O(k), We use a max heap of size k to keep track of the k largest elements in the binary search tree.
Therefore, the overall space complexity of this approach is O(k).
Share your thoughts in the comments
Please Login to comment...