Check if given sorted sub-sequence exists in binary search tree

Given a binary search tree and a sorted sub-sequence. the task is to check if the given sorted sub-sequence exist in binary search tree or not.

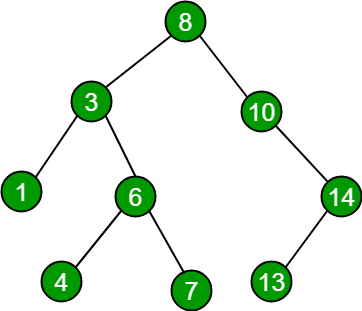
Examples:

// For above binary search tree
Input : seq[] = {4, 6, 8, 14}
Output: "Yes"

Input : seq[] = {4, 6, 8, 12, 13}
Output: "No"

A simple solution is to store inorder traversal in an auxiliary array and then by matching elements of sorted sub-sequence one by one with inorder traversal of tree , we can if sub-sequence exist in BST or not. Time complexity for this approach will be O(n) but it requires extra space O(n) for storing traversal in an array.
An efficient solution is to match elements of sub-sequence while we are traversing BST in inorder fashion. We take index as a iterator for given sorted sub-sequence and start inorder traversal of given bst, if current node matches with seq[index] then move index in forward direction by incrementing 1 and after complete traversal of BST if index==n that means all elements of given sub-sequence have been matched and exist as a sorted sub-sequence in given BST. 

C++

// C++ program to find if given array exists as a
// subsequence in BST
#include<bits/stdc++.h>
using namespace std;

// A binary Tree node
struct Node
{
    int data;
    struct Node *left, *right;
};

// A utility function to create a new BST node
// with key as given num
struct Node* newNode(int num)
{
    struct Node* temp = new Node;
    temp->data = num;
    temp->left = temp->right = NULL;
    return temp;
}

// A utility function to insert a given key to BST
struct Node* insert(struct Node* root, int key)
{
    if (root == NULL)
        return newNode(key);
    if (root->data > key)
        root->left = insert(root->left, key);
    else
        root->right = insert(root->right, key);
    return root;
}

// function to check if given sorted sub-sequence exist in BST
// index --> iterator for given sorted sub-sequence
// seq[] --> given sorted sub-sequence
void seqExistUtil(struct Node *ptr, int seq[], int &index)
{
    if (ptr == NULL)
        return;

    // We traverse left subtree first in Inorder
    seqExistUtil(ptr->left, seq, index);

    // If current node matches with se[index] then move
    // forward in sub-sequence
    if (ptr->data == seq[index])
        index++;

    // We traverse left subtree in the end in Inorder
    seqExistUtil(ptr->right, seq, index);
}

// A wrapper over seqExistUtil. It returns true
// if seq[0..n-1] exists in tree.
bool seqExist(struct Node *root, int seq[], int n)
{
    // Initialize index in seq[]
    int index = 0;

    // Do an inorder traversal and find if all
    // elements of seq[] were present
    seqExistUtil(root, seq, index);

    // index would become n if all elements of
    // seq[] were present
    return (index == n);
}

// driver program to run the case
int main()
{
    struct Node* root = NULL;
    root = insert(root, 8);
    root = insert(root, 10);
    root = insert(root, 3);
    root = insert(root, 6);
    root = insert(root, 1);
    root = insert(root, 4);
    root = insert(root, 7);
    root = insert(root, 14);
    root = insert(root, 13);

    int seq[] = {4, 6, 8, 14};
    int n = sizeof(seq)/sizeof(seq[0]);

    seqExist(root, seq, n)? cout << "Yes" :
                            cout << "No";

    return 0;
}

Java

// Java program to find if given array
// exists as a subsequence in BST
import java.util.*;

class GFG
{

// A binary Tree node
static class Node
{
    int data;
    Node left, right;
};

//structure of int class
static class INT
{
    int a;
}

// A utility function to create a new BST node
// with key as given num
static Node newNode(int num)
{
    Node temp = new Node();
    temp.data = num;
    temp.left = temp.right = null;
    return temp;
}

// A utility function to insert a given key to BST
static Node insert( Node root, int key)
{
    if (root == null)
        return newNode(key);
    if (root.data > key)
        root.left = insert(root.left, key);
    else
        root.right = insert(root.right, key);
    return root;
}

// function to check if given sorted
// sub-sequence exist in BST index -.
// iterator for given sorted sub-sequence
// seq[] -. given sorted sub-sequence
static void seqExistUtil( Node ptr, int seq[], INT index)
{
    if (ptr == null)
        return;

    // We traverse left subtree
    // first in Inorder
    seqExistUtil(ptr.left, seq, index);

    // If current node matches
    // with se[index] then move
    // forward in sub-sequence
    if (ptr.data == seq[index.a])
        index.a++;

    // We traverse left subtree
    // in the end in Inorder
    seqExistUtil(ptr.right, seq, index);
}

// A wrapper over seqExistUtil.
// It returns true if seq[0..n-1]
// exists in tree.
static boolean seqExist( Node root, int seq[], int n)
{
    // Initialize index in seq[]
    INT index = new INT();

    index.a = 0;

    // Do an inorder traversal and find if all
    // elements of seq[] were present
    seqExistUtil(root, seq, index);

    // index would become n if all
    // elements of seq[] were present
    return (index.a == n);
}

// Driver code
public static void main(String args[])
{
    Node root = null;
    root = insert(root, 8);
    root = insert(root, 10);
    root = insert(root, 3);
    root = insert(root, 6);
    root = insert(root, 1);
    root = insert(root, 4);
    root = insert(root, 7);
    root = insert(root, 14);
    root = insert(root, 13);

    int seq[] = {4, 6, 8, 14};
    int n = seq.length;

    if(seqExist(root, seq, n))
        System.out.println("Yes");
    else
        System.out.println("No");
}
}

// This code is contributed by Arnab Kundu

Python3

# Python3 program to find if given array
# exists as a subsequence in BST
class Node:

    # Constructor to create a new node
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# A utility function to insert a
# given key to BST
def insert(root, key):
    if root == None:
        return Node(key)
    if root.data > key:
        root.left = insert(root.left, key)
    else:
        root.right = insert(root.right, key)
    return root

# function to check if given sorted
# sub-sequence exist in BST index .
# iterator for given sorted sub-sequence
# seq[] . given sorted sub-sequence
def seqExistUtil(ptr, seq, index):
    if ptr == None:
        return

    # We traverse left subtree
    # first in Inorder
    seqExistUtil(ptr.left, seq, index)

    # If current node matches with se[index[0]]
    # then move forward in sub-sequence
    if ptr.data == seq[index[0]]:
        index[0] += 1

    # We traverse left subtree in
    # the end in Inorder
    seqExistUtil(ptr.right, seq, index)

# A wrapper over seqExistUtil. It returns
# true if seq[0..n-1] exists in tree.
def seqExist(root, seq, n):

    # Initialize index in seq[]
    index = [0]

    # Do an inorder traversal and find if
    # all elements of seq[] were present
    seqExistUtil(root, seq, index)

    # index would become n if all elements
    # of seq[] were present
    if index[0] == n:
        return True
    else:
        return False

# Driver Code
if __name__ == '__main__':
    root = None
    root = insert(root, 8)
    root = insert(root, 10)
    root = insert(root, 3)
    root = insert(root, 6)
    root = insert(root, 1)
    root = insert(root, 4)
    root = insert(root, 7)
    root = insert(root, 14)
    root = insert(root, 13)

    seq = [4, 6, 8, 14]
    n = len(seq)
    if seqExist(root, seq, n):
        print("Yes")
    else:
        print("No")

# This code is contributed by PranchalK

C#

// C# program to find if given array
// exists as a subsequence in BST
using System;

class GFG
{

// A binary Tree node
public class Node
{
    public int data;
    public Node left, right;
};

// structure of int class
public class INT
{
    public int a;
}

// A utility function to create a new BST node
// with key as given num
static Node newNode(int num)
{
    Node temp = new Node();
    temp.data = num;
    temp.left = temp.right = null;
    return temp;
}

// A utility function to insert a given key to BST
static Node insert( Node root, int key)
{
    if (root == null)
        return newNode(key);
    if (root.data > key)
        root.left = insert(root.left, key);
    else
        root.right = insert(root.right, key);
    return root;
}

// function to check if given sorted
// sub-sequence exist in BST index -.
// iterator for given sorted sub-sequence
// seq[] -. given sorted sub-sequence
static void seqExistUtil( Node ptr, int []seq, INT index)
{
    if (ptr == null)
        return;

    // We traverse left subtree
    // first in Inorder
    seqExistUtil(ptr.left, seq, index);

    // If current node matches
    // with se[index] then move
    // forward in sub-sequence
    if (ptr.data == seq[index.a])
        index.a++;

    // We traverse left subtree
    // in the end in Inorder
    seqExistUtil(ptr.right, seq, index);
}

// A wrapper over seqExistUtil.
// It returns true if seq[0..n-1]
// exists in tree.
static bool seqExist( Node root, int []seq, int n)
{
    // Initialize index in seq[]
    INT index = new INT();

    index.a = 0;

    // Do an inorder traversal and find if all
    // elements of seq[] were present
    seqExistUtil(root, seq, index);

    // index would become n if all
    // elements of seq[] were present
    return (index.a == n);
}

// Driver code
public static void Main(String []args)
{
    Node root = null;
    root = insert(root, 8);
    root = insert(root, 10);
    root = insert(root, 3);
    root = insert(root, 6);
    root = insert(root, 1);
    root = insert(root, 4);
    root = insert(root, 7);
    root = insert(root, 14);
    root = insert(root, 13);

    int []seq = {4, 6, 8, 14};
    int n = seq.Length;

    if(seqExist(root, seq, n))
        Console.WriteLine("Yes");
    else
        Console.WriteLine("No");
}
}

/* This code contributed by PrinciRaj1992 */

Javascript

<script>

// JavaScript program to find if given array
// exists as a subsequence in BST


// A binary Tree node
class Node
{
    constructor()
    {
        this.data = 0;
        this.left = null;
        this.right = null;
    }
};

// structure of int class
class INT
{
    constructor()
    {
        this.a = 0;
    }
}

// A utility function to create a new BST node
// with key as given num
function newNode(num)
{
    var temp = new Node();
    temp.data = num;
    temp.left = temp.right = null;
    return temp;
}

// A utility function to insert a given key to BST
function insert( root, key)
{
    if (root == null)
        return newNode(key);
    if (root.data > key)
        root.left = insert(root.left, key);
    else
        root.right = insert(root.right, key);
    return root;
}

// function to check if given sorted
// sub-sequence exist in BST index -.
// iterator for given sorted sub-sequence
// seq[] -. given sorted sub-sequence
function seqExistUtil( ptr, seq, index)
{
    if (ptr == null)
        return;

    // We traverse left subtree
    // first in Inorder
    seqExistUtil(ptr.left, seq, index);

    // If current node matches
    // with se[index] then move
    // forward in sub-sequence
    if (ptr.data == seq[index.a])
        index.a++;

    // We traverse left subtree
    // in the end in Inorder
    seqExistUtil(ptr.right, seq, index);
}

// A wrapper over seqExistUtil.
// It returns true if seq[0..n-1]
// exists in tree.
function seqExist( root, seq, n)
{
    // Initialize index in seq[]
    var index = new INT();

    index.a = 0;

    // Do an inorder traversal and find if all
    // elements of seq[] were present
    seqExistUtil(root, seq, index);

    // index would become n if all
    // elements of seq[] were present
    return (index.a == n);
}

// Driver code
var root = null;
root = insert(root, 8);
root = insert(root, 10);
root = insert(root, 3);
root = insert(root, 6);
root = insert(root, 1);
root = insert(root, 4);
root = insert(root, 7);
root = insert(root, 14);
root = insert(root, 13);
var seq = [4, 6, 8, 14];
var n = seq.length;
if(seqExist(root, seq, n))
    document.write("Yes");
else
    document.write("No");

</script>

Output:

Yes

Time complexity: O(n)

Auxiliary Space: O(n) for call stack since using recursion, where n is total no of nodes in BST

This article is contributed by Shashank Mishra ( Gullu ). If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.