Largest number in BST which is less than or equal to N
We have a binary search tree and a number N. Our task is to find the greatest number in the binary search tree that is less than or equal to N. Print the value of the element if it exists otherwise print -1.
Examples:
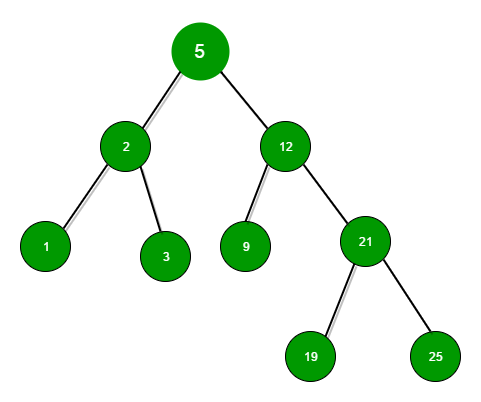
For the above given binary search tree-
Input : N = 24 Output :result = 21 (searching for 24 will be like-5->12->21) Input : N = 4 Output : result = 3 (searching for 4 will be like-5->2->3)
We follow recursive approach for solving this problem. We start searching for element from root node. If we reach a leaf and its value is greater than N, element does not exist so return -1. Else if node’s value is less than or equal to N and right value is NULL or greater than N, then return the node value as it will be the answer.
Otherwise if node’s value is greater than N, then search for the element in the left subtree else search for the element in the right subtree by calling the same function by passing the left or right values accordingly.
Implementation:
C++
// C++ code to find the largest value smaller// than or equal to N#include <bits/stdc++.h>using namespace std;struct Node { int key; Node *left, *right;};// To create new BST NodeNode* newNode(int item){ Node* temp = new Node; temp->key = item; temp->left = temp->right = NULL; return temp;}// To insert a new node in BSTNode* insert(Node* node, int key){ // if tree is empty return new node if (node == NULL) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); // return the (unchanged) node pointer return node;}// function to find max value less than Nint findMaxforN(Node* root, int N){ // Base cases if (root == NULL) return -1; if (root->key == N) return N; // If root's value is smaller, try in right // subtree else if (root->key < N) { int k = findMaxforN(root->right, N); if (k == -1) return root->key; else return k; } // If root's key is greater, return value // from left subtree. else if (root->key > N) return findMaxforN(root->left, N); }// Driver codeint main(){ int N = 4; // creating following BST /* 5 / \ 2 12 / \ / \ 1 3 9 21 / \ 19 25 */ Node* root = insert(root, 25); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); printf("%d", findMaxforN(root, N)); return 0;} |
Java
// Java code to find the largest value smaller// than or equal to Nclass GfG {static class Node { int key; Node left, right;}// To create new BST Nodestatic Node newNode(int item){ Node temp = new Node(); temp.key = item; temp.left = null; temp.right = null; return temp;}// To insert a new node in BSTstatic Node insert(Node node, int key){ // if tree is empty return new node if (node == null) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); // return the (unchanged) node pointer return node;}// function to find max value less than Nstatic int findMaxforN(Node root, int N){ // Base cases if (root == null) return -1; if (root.key == N) return N; // If root's value is smaller, try in right // subtree else if (root.key < N) { int k = findMaxforN(root.right, N); if (k == -1) return root.key; else return k; } // If root's key is greater, return value // from left subtree. else if (root.key > N) return findMaxforN(root.left, N); return -1;}// Driver codepublic static void main(String[] args){ int N = 4; // creating following BST /* 5 / \ 2 12 / \ / \ 1 3 9 21 / \ 19 25 */ Node root = null; root = insert(root, 25); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); System.out.println(findMaxforN(root, N));}} |
Python3
# Python3 code to find the largest# value smaller than or equal to Nclass newNode: # Constructor to create a new node def __init__(self, data): self.key = data self.left = None self.right = None# To insert a new node in BSTdef insert(node, key): # if tree is empty return new node if node == None: return newNode(key) # if key is less than or greater than # node value then recur down the tree if key < node.key: node.left = insert(node.left, key) elif key > node.key: node.right = insert(node.right, key) # return the (unchanged) node pointer return node# function to find max value less than Ndef findMaxforN(root, N): # Base cases if root == None: return -1 if root.key == N: return N # If root's value is smaller, try in # right subtree elif root.key < N: k = findMaxforN(root.right, N) if k == -1: return root.key else: return k # If root's key is greater, return # value from left subtree. elif root.key > N: return findMaxforN(root.left, N)# Driver codeif __name__ == '__main__': N = 4 # creating following BST # # 5 # / \ # 2 12 # / \ / \ # 1 3 9 21 # / \ # 19 25 root = None root = insert(root, 25) insert(root, 2) insert(root, 1) insert(root, 3) insert(root, 12) insert(root, 9) insert(root, 21) insert(root, 19) insert(root, 25) print(findMaxforN(root, N))# This code is contributed by PranchalK |
C#
// C# code to find the largest value// smaller than or equal to Nusing System;class GFG{ class Node { public int key; public Node left, right; } // To create new BST Node static Node newNode(int item) { Node temp = new Node(); temp.key = item; temp.left = null; temp.right = null; return temp; } // To insert a new node in BST static Node insert(Node node, int key) { // if tree is empty return new node if (node == null) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); // return the (unchanged) node pointer return node; } // function to find max value less than N static int findMaxforN(Node root, int N) { // Base cases if (root == null) return -1; if (root.key == N) return N; // If root's value is smaller, // try in right subtree else if (root.key < N) { int k = findMaxforN(root.right, N); if (k == -1) return root.key; else return k; } // If root's key is greater, return // value from left subtree. else if (root.key > N) return findMaxforN(root.left, N); return -1; } // Driver code public static void Main(String[] args) { int N = 4; // creating following BST /* 5 / \ 2 12 / \ / \ 1 3 9 21 / \ 19 25 */ Node root = null; root = insert(root, 25); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); Console.WriteLine(findMaxforN(root, N)); }}// This code is contributed 29AjayKumar |
Javascript
<script>// javascript code to find the largest value smaller// than or equal to N class Node { constructor(){ this.key = 0; this.left = null,this.right = null; } } // To create new BST Node function newNode(item) { var temp = new Node(); temp.key = item; temp.left = null; temp.right = null; return temp; } // To insert a new node in BST function insert(node , key) { // if tree is empty return new node if (node == null) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); // return the (unchanged) node pointer return node; } // function to find max value less than N function findMaxforN(root , N) { // Base cases if (root == null) return -1; if (root.key == N) return N; // If root's value is smaller, try in right // subtree else if (root.key < N) { var k = findMaxforN(root.right, N); if (k == -1) return root.key; else return k; } // If root's key is greater, return value // from left subtree. else if (root.key > N) return findMaxforN(root.left, N); return -1; } // Driver code var N = 4; // creating following BST /* * 5 / \ 2 12 / \ / \ 1 3 9 21 / \ 19 25 */var root = null; root = insert(root, 25); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); document.write(findMaxforN(root, N));// This code is contributed by Rajput-Ji</script> |
Output
3
Time Complexity: O(h), where h is height of BST.
Auxiliary Space: O(h), The extra space is used in recursion call stack.
Iterative Solution: Below is an iterative solution and it does not require extra space for recursion call stack.
Implementation:
C++
// C++ code to find the largest value smaller// than or equal to N#include <bits/stdc++.h>using namespace std;struct Node { int key; Node *left, *right;};// To create new BST NodeNode* newNode(int item){ Node* temp = new Node; temp->key = item; temp->left = temp->right = NULL; return temp;}// To insert a new node in BSTNode* insert(Node* node, int key){ // if tree is empty return new node if (node == NULL) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); // return the (unchanged) node pointer return node;}// function to find max value less than Nvoid findMaxforN(Node* root, int N){ // Start from root and keep looking for larger while (root != NULL && root->right != NULL) { // If root is smaller go to right side if (N > root->key && N >= root->right->key) root = root->right; // If root is greater go to left side else if (N < root->key) root = root->left; else break; } if (root == NULL || root->key > N) cout << -1; else cout << root->key;}// Driver codeint main(){ int N = 50; Node* root = insert(root, 5); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); findMaxforN(root, N); return 0;} |
Java
// Java code to find the largest value smaller// than or equal to Nimport java.util.*;class GFG{ static class Node { int key; Node left, right; }; // To create new BST Node static Node newNode(int item) { Node temp = new Node(); temp.key = item; temp.left = temp.right = null; return temp; } // To insert a new node in BST static Node insert(Node node, int key) { // if tree is empty return new node if (node == null) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); // return the (unchanged) node pointer return node; } // function to find max value less than N static void findMaxforN(Node root, int N) { // Start from root and keep looking for larger while (root != null && root.right != null) { // If root is smaller go to right side if (N > root.key && N >= root.right.key) root = root.right; // If root is greater go to left side else if (N < root.key) root = root.left; else break; } if (root == null || root.key > N) System.out.print(-1); else System.out.print(root.key); } // Driver code public static void main(String[] args) { int N = 50; Node root = insert(null, 5); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); findMaxforN(root, N); }}// This code is contributed by Rajput-Ji |
Python3
# Python3 code to find the largest value# smaller than or equal to Nclass newNode: # To create new BST Node def __init__(self, data): self.key = data self.left = None self.right = None# To insert a new node in BSTdef insert(node, key): # If tree is empty return new node if (node == None): return newNode(key) # If key is less than or greater than # node value then recur down the tree if (key < node.key): node.left = insert(node.left, key) elif (key > node.key): node.right = insert(node.right, key) # Return the (unchanged) node pointer return node# Function to find max value less than Ndef findMaxforN(root, N): # Start from root and keep looking for larger while (root != None and root.right != None): # If root is smaller go to right side if (N > root.key and N >= root.right.key): root = root.right # If root is greater go to left side elif (N < root.key): root = root.left else: break if (root == None or root.key > N): print(-1) else: print(root.key)# Driver codeif __name__ == '__main__': N = 50 root = None root = insert(root, 5) insert(root, 2) insert(root, 1) insert(root, 3) insert(root, 12) insert(root, 9) insert(root, 21) insert(root, 19) insert(root, 25) findMaxforN(root, N)# This code is contributed by bgangwar59 |
C#
// C# code to find the largest value smaller// than or equal to Nusing System;public class GFG { public class Node { public int key; public Node left, right; }; // To create new BST Node static Node newNode(int item) { Node temp = new Node(); temp.key = item; temp.left = temp.right = null; return temp; } // To insert a new node in BST static Node insert(Node node, int key) { // if tree is empty return new node if (node == null) return newNode(key); // if key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key > node.key) node.right = insert(node.right, key); // return the (unchanged) node pointer return node; } // function to find max value less than N static void findMaxforN(Node root, int N) { // Start from root and keep looking for larger while (root != null && root.right != null) { // If root is smaller go to right side if (N > root.key && N >= root.right.key) root = root.right; // If root is greater go to left side else if (N < root.key) root = root.left; else break; } if (root == null || root.key > N) Console.Write(-1); else Console.Write(root.key); } // Driver code public static void Main(String[] args) { int N = 50; Node root = insert(null, 5); insert(root, 2); insert(root, 1); insert(root, 3); insert(root, 12); insert(root, 9); insert(root, 21); insert(root, 19); insert(root, 25); findMaxforN(root, N); }}// This code is contributed by Rajput-Ji |
Javascript
<script>// JavaScript code to find the largest value smaller// than or equal to Nclass Node{ constructor(data) { this.key=data; this.left=this.right=null; }}function insert(node, key){ // If tree is empty return new node if (node == null) return new Node(key) // If key is less than or greater than // node value then recur down the tree if (key < node.key) node.left = insert(node.left, key) else if (key > node.key) node.right = insert(node.right, key) // Return the (unchanged) node pointer return node}function findMaxforN(root, N){ // Start from root and keep looking for larger while (root != null && root.right != null) { // If root is smaller go to right side if (N > root.key && N >= root.right.key) root = root.right // If root is greater go to left side else if (N < root.key) root = root.left else break } if (root == null || root.key > N) document.write(-1) else document.write(root.key)}let N = 50;let root = null;root=insert(root, 2)root=insert(root, 1)root=insert(root, 3)root=insert(root, 12)root=insert(root, 9)root=insert(root, 21)root=insert(root, 19)root=insert(root, 25)findMaxforN(root, N) // This code is contributed by rag2127</script> |
Output
25
Time Complexity: O(h), where h is height of BST.
Auxiliary Space: O(1), As constant extra space is used.
This article is contributed by Niteesh Kumar. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please Login to comment...