Given an integer array containing digits from [0, 9], the task is to print all possible letter combinations that the numbers could represent.
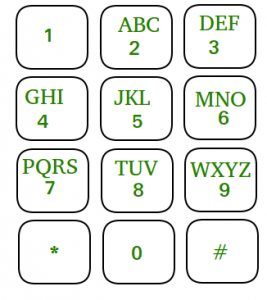
A mapping of digit to letters (just like on the telephone buttons) is being followed. Note that 0 and 1 do not map to any letters. All the mapping are shown in the image below:
Example:
Input: arr[] = {2, 3}
Output: ad ae af bd be bf cd ce cf
Input: arr[] = {9}
Output: w x y z
Approach: Now let us think how we would approach this problem without doing it in an iterative way. A recursive solution is intuitive and common. We keep adding each possible letter recursively and this will generate all the possible strings.
Let us think about how we can build an iterative solution using the recursive one. Recursion is possible through the use of a stack. So if we use a stack instead of a recursive function will that be an iterative solution? One could say so speaking technically but we then aren’t really doing anything different in terms of logic.
A Stack is a LIFO DS. Can we use another Data structure? What will be the difference if we use a FIFO DS? Let’s say a queue. Since BFS is done by queue and DFS by stack is there any difference between the two?
The difference between DFS and BFS is similar to this question. In DFS we will find each path possible in the tree one by one. It will perform all steps for a path first whereas BFS will build all paths together one step at a time.
So, a queue would work perfectly for this question. The only difference between the two algorithms using queue and stack will be the way in which they are formed. Stack will form all strings completely one by one whereas the queue will form all the strings together i.e. after x number of passes all the strings will have a length of x.
For example:
If the given number is "23",
then using queue, the letter combinations
obtained will be:
["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]
and using stack, the letter combinations obtained will
be:
["cf","ce","cd","bf","be","bd","af","ae","ad"].
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<string> letterCombinationsUtil(const int number[],
int n,
const string table[])
{
vector<string> list;
queue<string> q;
q.push("");
while (!q.empty()) {
string s = q.front();
q.pop();
if (s.length() == n)
list.push_back(s);
else
for (auto letter : table[number[s.length()]])
q.push(s + letter);
}
return list;
}
void letterCombinations(const int number[], int n)
{
string table[10]
= { "0", "1", "abc", "def", "ghi",
"jkl", "mno", "pqrs", "tuv", "wxyz" };
vector<string> list
= letterCombinationsUtil(number, n, table);
for (auto word : list)
cout << word << " ";
return;
}
int main()
{
int number[] = { 2, 3 };
int n = sizeof(number) / sizeof(number[0]);
letterCombinations(number, n);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static ArrayList<String>
letterCombinationsUtil(int[] number, int n,
String[] table)
{
ArrayList<String> list = new ArrayList<>();
Queue<String> q = new LinkedList<>();
q.add("");
while (!q.isEmpty()) {
String s = q.remove();
if (s.length() == n)
list.add(s);
else {
String val = table[number[s.length()]];
for (int i = 0; i < val.length(); i++)
{
q.add(s + val.charAt(i));
}
}
}
return list;
}
static void letterCombinations(int[] number, int n)
{
String[] table
= { "0", "1", "abc", "def", "ghi",
"jkl", "mno", "pqrs", "tuv", "wxyz" };
ArrayList<String> list
= letterCombinationsUtil(number, n, table);
for (int i = 0; i < list.size(); i++) {
System.out.print(list.get(i) + " ");
}
}
public static void main(String args[])
{
int[] number = { 2, 3 };
int n = number.length;
letterCombinations(number, n);
}
}
|
Python3
from collections import deque
def letterCombinationsUtil(number, n, table):
list = []
q = deque()
q.append("")
while len(q) != 0:
s = q.pop()
if len(s) == n:
list.append(s)
else:
for letter in table[number[len(s)]]:
q.append(s + letter)
return list
def letterCombinations(number, n):
table = ["0", "1", "abc", "def", "ghi", "jkl",
"mno", "pqrs", "tuv", "wxyz"]
list = letterCombinationsUtil(number, n, table)
s = ""
for word in list:
s += word + " "
print(s)
return
number = [2, 3]
n = len(number)
letterCombinations(number, n)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static List<String>
letterCombinationsUtil(int[] number, int n,
String[] table)
{
List<String> list = new List<String>();
Queue<String> q = new Queue<String>();
q.Enqueue("");
while (q.Count != 0) {
String s = q.Dequeue();
if (s.Length == n)
list.Add(s);
else {
String val = table[number[s.Length]];
for (int i = 0; i < val.Length; i++) {
q.Enqueue(s + val[i]);
}
}
}
return list;
}
static void letterCombinations(int[] number, int n)
{
String[] table
= { "0", "1", "abc", "def", "ghi",
"jkl", "mno", "pqrs", "tuv", "wxyz" };
List<String> list
= letterCombinationsUtil(number, n, table);
for (int i = 0; i < list.Count; i++) {
Console.Write(list[i] + " ");
}
}
public static void Main(String[] args)
{
int[] number = { 2, 3 };
int n = number.Length;
letterCombinations(number, n);
}
}
|
Javascript
</script>
function letterCombinations(digits) {
if(digits == ""){
return [];
}
let table = [ '0','1','abc','def','ghi','jkl','mno','pqrs','tuv','wxyz'];
let res =[];
let que = [''];
while(que.length>0){
let str = que[0];
que.shift();
if(str.length == digits.length){
res.push(str);
} else{
let s= Number(digits.charAt(str.length));
let val = table[s];
for(i=0;i<val.length;i++){
que.push(str+val.charAt(i));
}
}
}
return res;
}
let str = "23";
document.write(letterCombinations(str));
</script>
|
Outputad ae af bd be bf cd ce cf
Time Complexity: O(4^n) as we get set of all possible numbers of length n. In worst case, for each number there can be 4 possibilities.
Auxiliary Space: O(4^n)