Iterative Depth First Traversal of Graph
Last Updated :
29 Dec, 2022
Depth First Traversal (or Search) for a graph is similar to Depth First Traversal (DFS) of a tree. The only catch here is, unlike trees, graphs may contain cycles, so a node might be visited twice. To avoid processing a node more than once, use a boolean visited array.
Example:
Input: n = 4, e = 6
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3
Output: DFS from vertex 1 : 1 2 0 3
Explanation:
DFS Diagram:
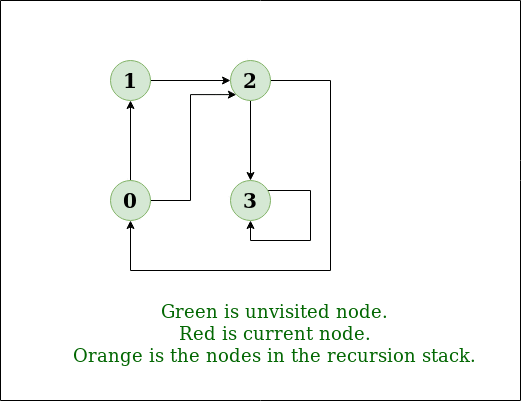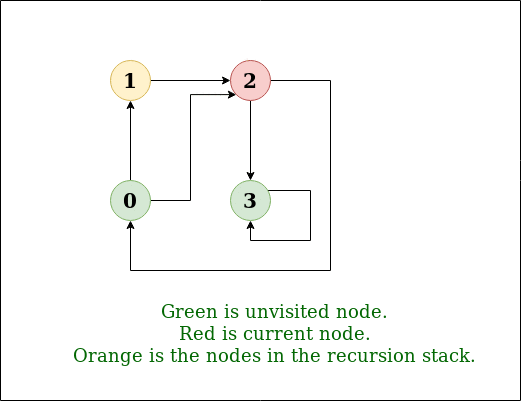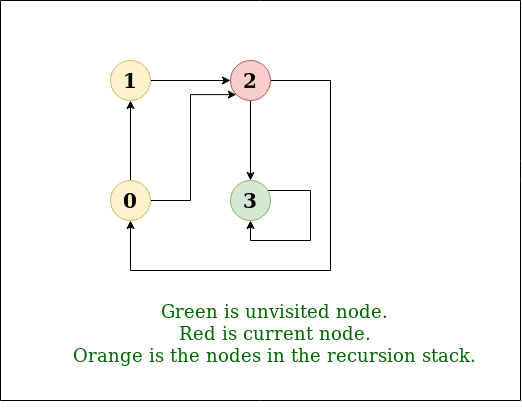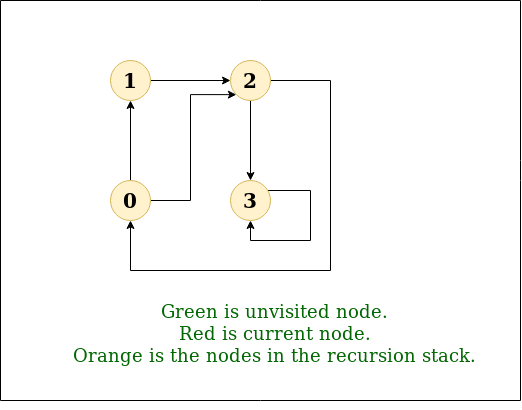
Input: n = 4, e = 6
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3
Output: DFS from vertex 2 : 2 0 1 3
Explanation:
DFS Diagram:
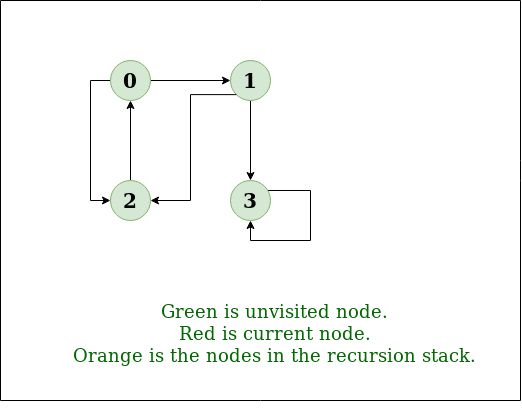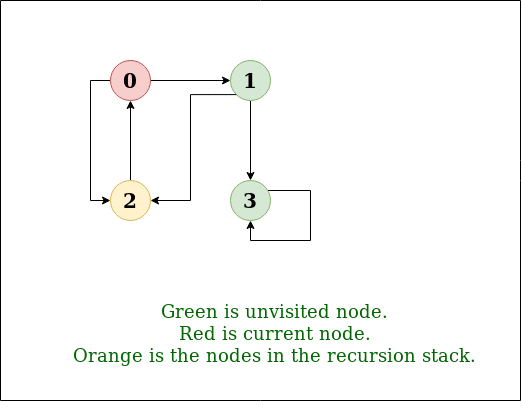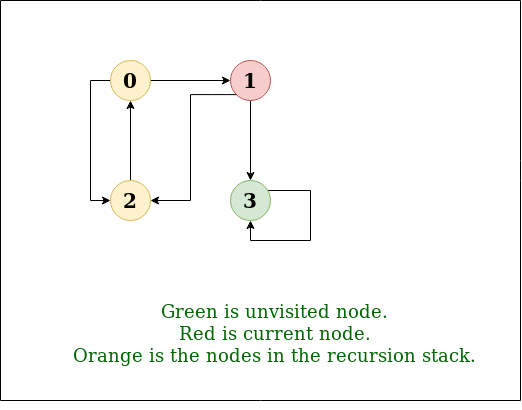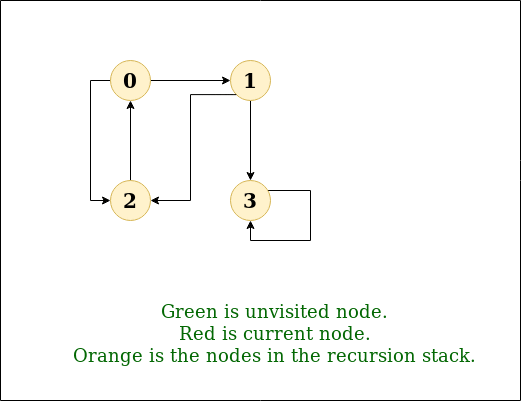
The recursive implementation of DFS is already discussed: previous post.
Solution:
- Approach: Depth-first search is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. So the basic idea is to start from the root or any arbitrary node and mark the node and move to the adjacent unmarked node and continue this loop until there is no unmarked adjacent node. Then backtrack and check for other unmarked nodes and traverse them. Finally print the nodes in the path.
The only difference between iterative DFS and recursive DFS is that the recursive stack is replaced by a stack of nodes.
- Algorithm:
- Created a stack of nodes and visited array.
- Insert the root in the stack.
- Run a loop till the stack is not empty.
- Pop the element from the stack and print the element.
- For every adjacent and unvisited node of current node, mark the node and insert it in the stack.
- Implementation of Iterative DFS: This is similar to BFS, the only difference is queue is replaced by stack.
C++
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
public:
Graph(int V);
void addEdge(int v, int w);
void DFS(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
void Graph::DFS(int s)
{
vector<bool> visited(V, false);
stack<int> stack;
stack.push(s);
while (!stack.empty())
{
int s = stack.top();
stack.pop();
if (!visited[s])
{
cout << s << " ";
visited[s] = true;
}
for (auto i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visited[*i])
stack.push(*i);
}
}
int main()
{
Graph g(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(1, 4);
cout << "Following is Depth First Traversal\n";
g.DFS(0);
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static class Graph
{
int V;
LinkedList<Integer>[] adj;
Graph(int V)
{
this.V = V;
adj = new LinkedList[V];
for (int i = 0; i < adj.length; i++)
adj[i] = new LinkedList<Integer>();
}
void addEdge(int v, int w)
{
adj[v].add(w);
}
void DFS(int s)
{
Vector<Boolean> visited = new Vector<Boolean>(V);
for (int i = 0; i < V; i++)
visited.add(false);
Stack<Integer> stack = new Stack<>();
stack.push(s);
while(stack.empty() == false)
{
s = stack.peek();
stack.pop();
if(visited.get(s) == false)
{
System.out.print(s + " ");
visited.set(s, true);
}
Iterator<Integer> itr = adj[s].iterator();
while (itr.hasNext())
{
int v = itr.next();
if(!visited.get(v))
stack.push(v);
}
}
}
}
public static void main(String[] args)
{
Graph g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(1, 4);
System.out.println("Following is the Depth First Traversal");
g.DFS(0);
}
}
|
Python3
class Graph:
def __init__(self,V):
self.V = V
self.adj = [[] for i in range(V)]
def addEdge(self,v, w):
self.adj[v].append(w)
def DFS(self,s):
visited = [False for i in range(self.V)]
stack = []
stack.append(s)
while (len(stack)):
s = stack[-1]
stack.pop()
if (not visited[s]):
print(s,end=' ')
visited[s] = True
for node in self.adj[s]:
if (not visited[node]):
stack.append(node)
g = Graph(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(1, 4);
print("Following is Depth First Traversal")
g.DFS(0)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class Graph
{
public int V;
public LinkedList<int>[] adj;
public Graph(int V)
{
this.V = V;
adj = new LinkedList<int>[V];
for (int i = 0; i < adj.Length; i++)
adj[i] = new LinkedList<int>();
}
public void addEdge(int v, int w)
{
adj[v].AddLast(w);
}
public void DFS(int s)
{
Boolean []visited = new Boolean[V];
Stack<int> stack = new Stack<int>();
stack.Push(s);
while(stack.Count > 0)
{
s = stack.Peek();
stack.Pop();
if(visited[s] == false)
{
Console.Write(s + " ");
visited[s] = true;
}
foreach(int v in adj[s])
{
if(!visited[v])
stack.Push(v);
}
}
}
}
public static void Main(String []args)
{
Graph g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(1, 4);
Console.Write("Following is the Depth First Traversal\n");
g.DFS(0);
}
}
|
Javascript
<script>
class Graph{
constructor(V)
{
this.V = V;
this.adj = new Array(V);
for(let i = 0; i < this.adj.length; i++)
this.adj[i] = [];
}
addEdge(v, w)
{
this.adj[v].push(w);
}
DFS(s)
{
let visited = [];
for(let i = 0; i < this.V; i++)
visited.push(false);
let stack = [];
stack.push(s);
while(stack.length != 0)
{
s = stack.pop();
if (visited[s] == false)
{
document.write(s + " ");
visited[s] = true;
}
for(let node = 0;
node < this.adj[s].length;
node++)
{
if (!visited[this.adj[s][node]])
stack.push(this.adj[s][node])
}
}
}
}
let g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(0, 2);
g.addEdge(2, 1);
g.addEdge(0, 3);
g.addEdge(1, 4);
document.write("Following is the Depth " +
"First Traversal<br>");
g.DFS(0);
</script>
|
Output
Following is Depth First Traversal
0 3 2 1 4
- Complexity Analysis:
- Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
- Space Complexity: O(V). Since an extra visited array is needed of size V.
Modification of the above Solution: Note that the above implementation prints only vertices that are reachable from a given vertex. For example, if the edges 0-3 and 0-2 are removed, then the above program would only print 0. To print all vertices of a graph, call DFS for every unvisited vertex.
Implementation:
C++
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
public:
Graph(int V);
void addEdge(int v, int w);
void DFS();
void DFSUtil(int s, vector<bool> &visited);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
void Graph::DFSUtil(int s, vector<bool> &visited)
{
stack<int> stack;
stack.push(s);
while (!stack.empty())
{
int s = stack.top();
stack.pop();
if (!visited[s])
{
cout << s << " ";
visited[s] = true;
}
for (auto i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visited[*i])
stack.push(*i);
}
}
void Graph::DFS()
{
vector<bool> visited(V, false);
for (int i = 0; i < V; i++)
if (!visited[i])
DFSUtil(i, visited);
}
int main()
{
Graph g(5);
g.addEdge(1, 0);
g.addEdge(2, 1);
g.addEdge(3, 4);
g.addEdge(4, 0);
cout << "Following is Depth First Traversal\n";
g.DFS();
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static class Graph
{
int V;
LinkedList<Integer>[] adj;
Graph(int V)
{
this.V = V;
adj = new LinkedList[V];
for (int i = 0; i < adj.length; i++)
adj[i] = new LinkedList<Integer>();
}
void addEdge(int v, int w)
{
adj[v].add(w);
}
void DFSUtil(int s, Vector<Boolean> visited)
{
Stack<Integer> stack = new Stack<>();
stack.push(s);
while(stack.empty() == false)
{
s = stack.peek();
stack.pop();
if(visited.get(s) == false)
{
System.out.print(s + " ");
visited.set(s, true);
}
Iterator<Integer> itr = adj[s].iterator();
while (itr.hasNext())
{
int v = itr.next();
if(!visited.get(v))
stack.push(v);
}
}
}
void DFS()
{
Vector<Boolean> visited = new Vector<Boolean>(V);
for (int i = 0; i < V; i++)
visited.add(false);
for (int i = 0; i < V; i++)
if (!visited.get(i))
DFSUtil(i, visited);
}
}
public static void main(String[] args)
{
Graph g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(2, 1);
g.addEdge(3, 4);
g.addEdge(4, 0);
System.out.println("Following is Depth First Traversal");
g.DFS();
}
}
|
Python3
class Graph:
def __init__(self, V):
self.V = V
self.adj = [[] for i in range(V)]
def addEdge(self, v, w):
self.adj[v].append(w)
def DFSUtil(self, s, visited):
stack = []
stack.append(s)
while (len(stack) != 0):
s = stack.pop()
if (not visited[s]):
print(s, end = " ")
visited[s] = True
i = 0
while i < len(self.adj[s]):
if (not visited[self.adj[s][i]]):
stack.append(self.adj[s][i])
i += 1
def DFS(self):
visited = [False] * self.V
for i in range(self.V):
if (not visited[i]):
self.DFSUtil(i, visited)
if __name__ == '__main__':
g = Graph(5)
g.addEdge(1, 0)
g.addEdge(2, 1)
g.addEdge(3, 4)
g.addEdge(4, 0)
print("Following is Depth First Traversal")
g.DFS()
|
C#
using System;
using System.Collections.Generic;
class GFG
{
class Graph
{
public int V;
public List<int>[] adj;
public Graph(int V)
{
this.V = V;
adj = new List<int>[V];
for (int i = 0; i < adj.Length; i++)
adj[i] = new List<int>();
}
public void addEdge(int v, int w)
{
adj[v].Add(w);
}
public void DFSUtil(int s, List<Boolean> visited)
{
Stack<int> stack = new Stack<int>();
stack.Push(s);
while(stack.Count != 0)
{
s = stack.Peek();
stack.Pop();
if(visited[s] == false)
{
Console.Write(s + " ");
visited[s] = true;
}
foreach(int itr in adj[s])
{
int v = itr;
if(!visited[v])
stack.Push(v);
}
}
}
public void DFS()
{
List<Boolean> visited = new List<Boolean>(V);
for (int i = 0; i < V; i++)
visited.Add(false);
for (int i = 0; i < V; i++)
if (!visited[i])
DFSUtil(i, visited);
}
}
public static void Main(String[] args)
{
Graph g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(2, 1);
g.addEdge(3, 4);
g.addEdge(4, 0);
Console.WriteLine("Following is Depth First Traversal");
g.DFS();
}
}
|
Javascript
<script>
class Graph
{
constructor(V)
{
this.V=V;
this.adj = new Array(V);
for (let i = 0; i < this.adj.length; i++)
this.adj[i] = [];
}
addEdge(v,w)
{
this.adj[v].push(w);
}
DFSUtil(s,visited)
{
let stack = [];
stack.push(s);
while(stack.length != 0)
{
s = stack.pop();
if(visited[s] == false)
{
document.write(s + " ");
visited[s] = true;
}
for (let itr=0;itr<this.adj[s].length;itr++)
{
let v = this.adj[s][itr];
if(!visited[v])
stack.push(v);
}
}
}
DFS()
{
let visited = []
for (let i = 0; i < this.V; i++)
visited.push(false);
for (let i = 0; i < this.V; i++)
if (!visited[i])
this.DFSUtil(i, visited);
}
}
let g = new Graph(5);
g.addEdge(1, 0);
g.addEdge(2, 1);
g.addEdge(3, 4);
g.addEdge(4, 0);
document.write("Following is Depth First Traversal<br>");
g.DFS();
</script>
|
Output
Following is Depth First Traversal
0 1 2 3 4
Time complexity: O(V+E), The time complexity of DFS is O (V+E). Here V is the number of vertices and E is the number of edges.
Auxiliary Space: O(V), The space complexity of DFS is O(V). The space is consumed by the recursion stack and the visited array.
Share your thoughts in the comments
Please Login to comment...