Iterative Postorder traversal | Set 3

We have seen different ways of performing postorder traversal on Binary Trees. 

• Post Order Traversal.
• Iterative Postorder Traversal using Two Stacks.
• Iterative Postorder Traversal using One Stack.

Here is another way of performing the postorder traversal on a Binary Tree iteratively using a single stack.
Consider the Below Terminologies: 

0 -  Left element
1 -  Right element
2 -  Node element

Following is the detailed algorithm: 

Take a Stack and perform the below operations:

1) Insert a pair of the root node as (node, 0).
2) Pop the top element to get the pair 
   (Let a = node and b be the variable)
    If b is equal to 0:
       Push another pair as (node, 1) and 
       Push the left child as (node->left, 0)
       Repeat Step 2
    Else If b is equal to 1:
       Push another pair as (node, 2) and 
       Push right child of node as (node->right, 0)
       Repeat Step 2
    Else If b is equal to 2:
       Print(node->data)
3) Repeat the above steps while stack is not empty

Consider the Below Binary Tree with just 3 nodes: 

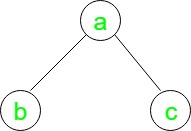
Illustration:

1) Push(a, 0)
   Stack - (a, 0)

2) top = (a, 0)
   Push(a, 1)
   Push(b, 0)
   Stack - (b, 0)
           (a, 1)

3) top = (b, 0)
   Push(b, 1)
   Stack - (b, 1)
           (a, 1)

4) top = (b, 1)
   Push(b, 2)
   Stack - (b, 2)
           (a, 1)

5) top = (b, 2)
   print(b)
   Stack -(a, 1)

6) top = (a, 1)
   push(a, 2)
   push(c, 0)
   Stack -  (c, 0)
            (a, 2)

7) top = (c, 0)
   push(c, 1)
   Stack - (c, 1)
            (a, 2)

8) top = (c, 1)
   push(c, 2)
   Stack - (c, 2)
            (a, 2)

9) top = (c, 2)
   print(c)
   Stack - (a, 2)

10) top = (a, 2)
    print(a)
    Stack - empty()

Below is the implementation of the above approach: 

C++

// C++ program to print postorder traversal
// iteratively

#include <bits/stdc++.h>
using namespace std;

// Binary Tree Node
struct Node {
    int data;
    struct Node* left;
    struct Node* right;
};

// Helper function to create a
// new Binary Tree node
struct Node* newNode(int data)
{
    struct Node* node = new Node;
    node->data = data;
    node->left = NULL;
    node->right = NULL;
    return (node);
}

// Function to perform postorder
// traversal iteratively
void iterativePostorder(Node* root)
{
    stack<pair<Node*, int> > st;
    st.push(make_pair(root, 0));

    while (!st.empty()) {
        struct Node* temp = st.top().first;
        int b = st.top().second;
        st.pop();

        if (temp == NULL)
            continue;

        if (b == 0) {
            st.push(make_pair(temp, 1));

            if (temp->left != NULL)
                st.push(make_pair(temp->left, 0));
        }
        else if (b == 1) {
            st.push(make_pair(temp, 2));

            if (temp->right != NULL)
                st.push(make_pair(temp->right, 0));
        }
        else
            cout << temp->data << " ";
    }
}

// Driver Code
int main()
{
    // Construct the below Binary Tree
    //        1
    //       / \
    //      2   3
    //    /   \
    //   4     5
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);

    iterativePostorder(root);

    return 0;
}

Java

// Java program to print postorder traversal
// iteratively
import java.util.*;

class GFG
{

//pair class
static class Pair
{
    Node first;
    int second;
    Pair(Node a,int b)
    {
        first = a;
        second = b;
    }
}

// Binary Tree Node
static class Node
{
    int data;
    Node left;
    Node right;
};

// Helper function to create a
// new Binary Tree node
static Node newNode(int data)
{
    Node node = new Node();
    node.data = data;
    node.left = null;
    node.right = null;
    return (node);
}

// Function to perform postorder
// traversal iteratively
static void iterativePostorder(Node root)
{
    Stack<Pair> st = new Stack<Pair>();
    st.add(new Pair(root, 0));

    while (st.size() > 0)
    {
        Node temp = st.peek().first;
        int b = st.peek().second;
        st.pop();

        if (temp == null)
            continue;

        if (b == 0)
        {
            st.add(new Pair(temp, 1));

            if (temp.left != null)
                st.add(new Pair(temp.left, 0));
        }
        else if (b == 1)
        {
            st.add(new Pair(temp, 2));

            if (temp.right != null)
                st.add(new Pair(temp.right, 0));
        }
        else
            System.out.print( temp.data + " ");
    }
}

// Driver Code
public static void main(String args[])
{
    // Construct the below Binary Tree
    //     1
    //     / \
    //     2 3
    // / \
    // 4     5
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);

    iterativePostorder(root);
}
}

// This code is contributed by Arnab Kundu

Python3

# Python program to print postorder traversal
# iteratively

# pair class
class Pair:
    def __init__(self, a, b):
        self.first = a
        self.second = b

# Binary Tree Node
class Node :
    def __init__(self):
        self.data = 0
        self.left = None
        self.right = None

# Helper function to create a
# new Binary Tree node
def newNode(data):

    node = Node()
    node.data = data
    node.left = None
    node.right = None
    return (node)

# Function to perform postorder
# traversal iteratively
def iterativePostorder( root):

    st = []
    st.append(Pair(root, 0))

    while (len(st)> 0):

        temp = st[-1].first
        b = st[-1].second
        st.pop()

        if (temp == None):
            continue

        if (b == 0) :
            st.append(Pair(temp, 1))

            if (temp.left != None):
                st.append(Pair(temp.left, 0))

        elif (b == 1):
            st.append(Pair(temp, 2))

            if (temp.right != None):
                st.append(Pair(temp.right, 0))

        else:
            print( temp.data ,end= " ")

# Driver Code

# Construct the below Binary Tree
#     1
#     / \
# 2 3
# / \
# 4 5
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)

iterativePostorder(root)

# This code is contributed by Arnab Kundu

C#

// C# program to print postorder traversal
// iteratively
using System;
using System.Collections.Generic;
class GFG
{

//pair class
public class Pair
{
    public Node first;
    public int second;
    public Pair(Node a,int b)
    {
        first = a;
        second = b;
    }
}

// Binary Tree Node
public class Node
{
    public int data;
    public Node left;
    public Node right;
};

// Helper function to create a
// new Binary Tree node
static Node newNode(int data)
{
    Node node = new Node();
    node.data = data;
    node.left = null;
    node.right = null;
    return (node);
}

// Function to perform postorder
// traversal iteratively
static void iterativePostorder(Node root)
{
    Stack<Pair> st = new Stack<Pair>();
    st.Push(new Pair(root, 0));

    while (st.Count > 0)
    {
        Node temp = st.Peek().first;
        int b = st.Peek().second;
        st.Pop();

        if (temp == null)
            continue;

        if (b == 0)
        {
            st.Push(new Pair(temp, 1));

            if (temp.left != null)
                st.Push(new Pair(temp.left, 0));
        }
        else if (b == 1)
        {
            st.Push(new Pair(temp, 2));

            if (temp.right != null)
                st.Push(new Pair(temp.right, 0));
        }
        else
            Console.Write(temp.data + " ");
    }
}

// Driver Code
public static void Main(String []args)
{
    // Construct the below Binary Tree
    //     1
    //     / \
    //     2 3
    // / \
    // 4     5
    Node root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);

    iterativePostorder(root);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

    // JavaScript program to print
    // postorder traversal iteratively

    // Binary Tree Node
    class Node
    {
        constructor(data) {
           this.left = null;
           this.right = null;
           this.data = data;
        }
    }

    // Helper function to create a
    // new Binary Tree node
    function newNode(data)
    {
        let node = new Node(data);
        return (node);
    }

    // Function to perform postorder
    // traversal iteratively
    function iterativePostorder(root)
    {
        let st = [];
        st.push([root, 0]);

        while (st.length > 0)
        {
            let temp = st[st.length - 1][0];
            let b = st[st.length - 1][1];
            st.pop();

            if (temp == null)
                continue;

            if (b == 0)
            {
                st.push([temp, 1]);

                if (temp.left != null)
                    st.push([temp.left, 0]);
            }
            else if (b == 1)
            {
                st.push([temp, 2]);

                if (temp.right != null)
                    st.push([temp.right, 0]);
            }
            else
                document.write(temp.data + " ");
        }
    }

    // Construct the below Binary Tree
    //     1
    //     / \
    //     2 3
    // / \
    // 4     5
    let root = newNode(1);
    root.left = newNode(2);
    root.right = newNode(3);
    root.left.left = newNode(4);
    root.left.right = newNode(5);

    iterativePostorder(root);

</script>

Output:

4 5 2 3 1

Time Complexity: O(N)
Auxiliary Space: O(N)