Introduction to Signals and Systems: Properties of systems

Difficulty Level : Hard
Last Updated : 30 Sep, 2022

Signal is an electric or electromagnetic current carrying data, that can be transmitted or received.

Mathematically represented as a function of an independent variable e.g. density, depth, etc. Therefore, a signal is a physical quantity that varies with time, space, or any other independent variable by which information can be conveyed. Here independent variable is time.

Types of time signals:

Continuous time signals x(t)- defined at every point in time
Discrete time signals x[n] – defined only at a discrete set of values of time (integer).

A System is any physical set of components or a function of several devices that takes a signal in input, and produces a signal as output.

Calculating Energy and Power of signals:

Energy– Square of amplitude/magnitude(if complex) over entire time domain.

for a continuous time signal-

$E=\int_{-\infty}^{\infty} |x(t)|^2 dt$

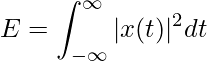
for a discrete time signal-

$E=\sum_{-\infty}^{\infty} |x[n]|^2$

Power- Rate of change of energy.

for a continuous time signal.

$P=\lim_{T\to\infty} 1/(2T) (\int_{-T}^{T} |x(t)|^2 dt)$

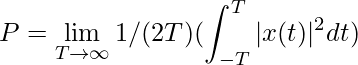
for a discrete time signal-

$P=\lim_{N\to\infty} 1/(2N+1) (\sum_{-N}^{N} |x[n]|^2)$

Classes of signals on the basis of their power and energy:

Energy signal– generally converging signals, aperiodic signals or signals that are bounded.
$E < \infty\ and\ P=0$
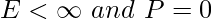
Power signal– generally periodic signals, as they encompass infinite area under their graph and extend from $+\infty$ to $-\infty$ .
$E \rightarrow \infty\ and\ P=constant$
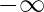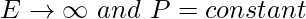
Neither energy nor power signal
$E \rightarrow \infty\ and\ P \rightarrow \infty$

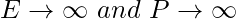
Transformation of the independent variable:

Shifting- the signal can be delayed ( x(t-T) ) or advanced ( x(t+T) ) by incrementing or decrementing the independent variable (time here).
The shape of the graph remains same only shifted on the time axis.
Scaling- the signal can be compressed ( x(at), a>1 ) or expanded ( x(t/a), a>1 or x(at), 1>a>0 ).
Here the shape/behaviour of the graph of the signal changes as the fundamental time period changes. In compression the time period decreases and in expansion the time period increases.
Reversal- also called folding as the graph is folded about the Y-axis or T if given x(T-t).

Properties of systems:

Periodicity- the signal’s behavior/graph repeats after every T. Therefore,
$x(t)=x(t+nT)\ or\ x(t)=x(t-nT)$
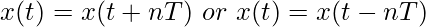
here T is the fundamental period
So we can say signal remains unchanged when shifted by multiples of T.
Even and Odd- an even signal is symmetric about the Y-axis.
x(t)=x(-t) even
x(t)=-x(-t) odd
A signal can be broken into it’s even and odd parts to make certain conversions easy.
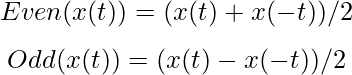
Linearity- constitutes of two properties-
(i) Additivity/Superposition-
if x1(t) -> y1(t)
and x2(t) -> y2(t)
$x1(t) + x2(t)\ \rightarrow y1(t) + y2(t)$
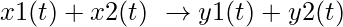
(ii) Property of scaling-
if x1(t) -> y1(t)
then
$a*x1(t)\ \rightarrow a*y1(t)$
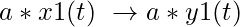
If both are satisfied, the system is linear.
Time invariant- Any delay provided in the input must be reflected in the output for a time invariant system.
$take \ x2(t)=x(t-T)$$ $$ then\ y(x2(t))\ must\ be\ =x2(y(t))$
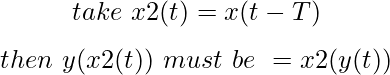
here x2(t) is a delayed input.
We check if putting a delayed input through the system is the same as a delay in the output signal.
LTI systems- A linear time invariant system. A system that is linear and time-invariant.
BIBO stability- The bounded input bounded output stability.
We say a system is BIBO stable if-
$\int_{-\infty}^{\infty} |x(t)| dt\ < \infty$
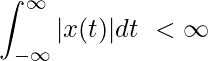
Causality- Causal signals are signals that are zero for all negative time.
If any value of the output signal depends on a future value of the input signal then the signal is non-causal.