Hashing in Distributed Systems
Last Updated :
02 Dec, 2022
Prerequisite – Hashing
A distributed system is a network that consists of autonomous computers that are connected using a distribution middleware. They help in sharing different resources and capabilities to provide users with a single and integrated coherent network.
One of the ways hashing can be implemented in a distributed system is by taking hash Modulo of a number of nodes.
The hash function can be defined as node_number = hash(key)mod_N where N is the number of Nodes.
To add/retrieve a key to/from the node, the client computes the hash value of that key and uses the result to contact the appropriate node by looking up its IP address. If the key is found, it is retrieved else it is added to the pool of the Node.
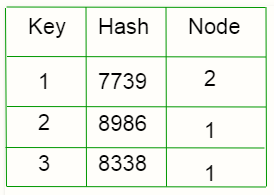
For example, a client wants to retrieve 1. Its hash value = 7739. It will go to Node number (7739%3). So, it will contact node 2. If the key is not found, it is added to the pool.
Disadvantage: The Rehashing problem.
Let’s suppose the number of nodes has changed. As the keys are distributed depending on the number of nodes, since the number of nodes has changed, the value from hashing function will change so the keys will be redistributed.
For example, let’s remove C
The allocated nodes for each key has changed.

For example, let’s add a new node D
The allocated nodes for each key has changed.

So, the distribution changes whenever we change the number of Nodes.
What happens is the more number of redistributions, the more number of misses, the more number of memory fetches, placing an additional load on the node and thus decreasing the performance.
Consistent Hashing.
The above issue can be solved by Consistent Hashing.
This method operates independently of the number of nodes as the hash function is not dependent on the number of nodes. Here we assume a chain/ring is formed and we place the keys as well as the nodes on the ring and distribute them.
The hash value can be computed as position_on_chain = hash(key)mod_360
(360 is chosen as we are representing things in a circle. And a circle has 360 degrees.)

Steps for the arrangement –
1) Find Hash values of the keys and place it on the ring according to the hash value.
2) Find Hash values of the individual nodes and place it on the ring according to the hash value.
3) Now map each key with the node which is closest to it in the counter-clockwise direction.
4) If the position of a node and key is same, assign that key to the node.
So, now to locate a node, we will just traverse the ring from the point of the position of the key till we find a node in the counter-clockwise direction.

Operations –
Case 1) Adding a node –
Suppose we add a new node D in the ring by calculating the hash. Only those keys will be redistributed whose values lie between the D and C. Now they will not point towards A, they will point towards D.

Case 2) Removing a node –
Suppose we remove a node C in the ring. Only those keys will be redistributed whose values lies between C and the B. Now they will not point towards C, they will point towards A.

This is how consistent hashing solves the rehashing problem. The number of keys which needs to be redistributed after rehashing is minimized. So, less number of memory fetches. Hence, performance is optimised.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...