Introduction:
Recurrent Neural Networks are those networks that deal with sequential data. They predict outputs using not only the current inputs but also by taking into consideration those that occurred before it. In other words, the current output depends on current output as well as a memory element (which takes into account the past inputs).
For training such networks, we use good old backpropagation but with a slight twist. We don’t independently train the system at a specific time
“t”. We train it at a specific time
“t” as well as all that has happened before time
“t” like t-1, t-2, t-3.
Consider the following representation of a RNN:

RNN Architecture
are the hidden states or memory units at time
t1, t2, t3 respectively, and
Ws is the weight matrix associated with it.
X1, X2, X3 are the inputs at time
t1, t2, t3 respectively, and
Wx is the weight matrix associated with it.
Y1, Y2, Y3 are the outputs at time
t1, t2, t3 respectively, and
Wy is the weight matrix associated with it.
For any time, t, we have the following two equations:
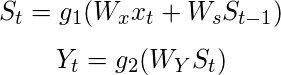
where g1 and g2 are activation functions.
Let us now perform back propagation at time t = 3.
Let the error function be:
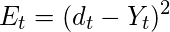
, so at t =3,
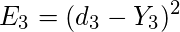
*We are using the squared error here, where
d3 is the desired output at time
t = 3.
To perform back propagation, we have to adjust the weights associated with inputs, the memory units and the outputs.
Adjusting Wy
For better understanding, let us consider the following representation:

Adjusting Wy
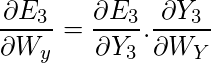
Explanation:
E3 is a function of
Y3. Hence, we differentiate
E3 w.r.t
Y3.
Y3 is a function of
WY. Hence, we differentiate
Y3 w.r.t
WY.
Adjusting Ws
For better understanding, let us consider the following representation:

Adjusting Ws
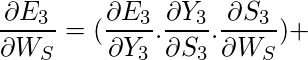
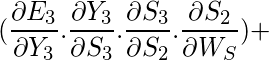
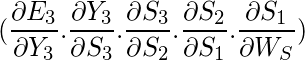
Explanation:
E3 is a function of
Y3. Hence, we differentiate
E3 w.r.t
Y3.
Y3 is a function of
S3. Hence, we differentiate
Y3 w.r.t
S3.
S3 is a function of
WS. Hence, we differentiate
S3 w.r.t
WS.
But we can’t stop with this; we also have to take into consideration, the previous time steps. So, we differentiate (partially) the Error function with respect to memory units
S2 as well as
S1 taking into consideration the weight matrix
WS.
We have to keep in mind that a memory unit, say S
t is a function of its previous memory unit S
t-1.
Hence, we differentiate
S3 with
S2 and
S2 with
S1.
Generally, we can express this formula as:
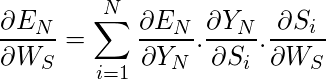
Adjusting WX:
For better understanding, let us consider the following representation:

Adjusting Wx
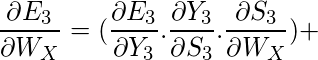
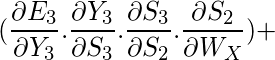
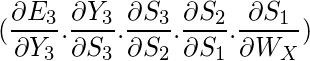
Explanation:
E3 is a function of
Y3. Hence, we differentiate
E3 w.r.t
Y3.
Y3 is a function of
S3. Hence, we differentiate
Y3 w.r.t
S3.
S3 is a function of
WX. Hence, we differentiate
S3 w.r.t
WX.
Again we can’t stop with this; we also have to take into consideration, the previous time steps. So, we differentiate (partially) the Error function with respect to memory units
S2 as well as
S1 taking into consideration the weight matrix WX.
Generally, we can express this formula as:
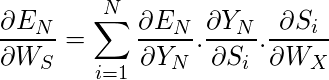
Limitations:
This method of Back Propagation through time (BPTT) can be used up to a limited number of time steps like 8 or 10. If we back propagate further, the gradient
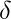
becomes too small. This problem is called the “Vanishing gradient” problem. The problem is that the contribution of information decays geometrically over time. So, if the number of time steps is >10 (Let’s say), that information will effectively be discarded.
Going Beyond RNNs:
One of the famous solutions to this problem is by using what is called Long Short-Term Memory (LSTM for short) cells instead of the traditional RNN cells. But there might arise yet another problem here, called the
exploding gradient problem, where the gradient grows uncontrollably large.
Solution: A popular method called gradient clipping can be used where in each time step, we can check if the gradient
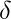
> threshold. If yes, then normalize it.
Share your thoughts in the comments
Please Login to comment...