Cross-Entropy Cost Functions used in Classification
Last Updated :
05 May, 2023
Cost functions play a crucial role in improving a Machine Learning model’s performance by being an integrated part of the gradient descent algorithm which helps us optimize the weights of a particular model. In this article, we will learn about one such cost function which is the cross-entropy function which is generally used for classification problems.
What is Entropy?
Entropy is a measure of the randomness or we can say uncertainty in the probability distribution of some specific target. If you have studied entropy in physics in your higher school then you must have encountered that the entropy of gases is higher than that of the solids because of the faster movement of particles in the latter which leads to a higher degree of randomness.
What is the difference between Entropy and Cross-Entropy?
Entropy just gives us the measure of the randomness in a particular probability distribution but the requirement is somewhat different here in machine learning which is to compare the difference between the probability distribution of the predicted probabilities and the true probabilities of the target variable. And for this case, the cross-entropy function comes in handy and serves the purpose.
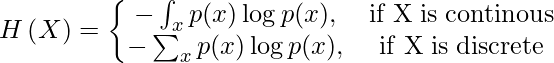
Due to this only we try to minimize the difference between the predicted and the actual probability distribution of the target variable. And as the value of the cost function decreases the performance of the Machine Learning model improves.
In the above-shown cost functions mathematical formula you must encounter a negative sign the significance of that is to make the values positive to avoid any confusion and better clarity. The original result without the negative sign will be negative because the probability values are between the range 0 to 1 and for these values the value of the logarithm is negative as can be seen from the below graph.

Logarithmic Function Range and Domain
Cross Entropy for Multi-class Classification
Now that we have a basic understanding of the theory and the mathematical formulation of the cross entropy function now let’s try to work on a sample problem to get a feel of how the value for the cross entropy cost function is calculated.
Example 1:
Actual Probabilities:
[0, 1, 0, 0]
Predicted Probabilities:
[0.21, 0.68, 0.09, 0.10]
Cross Entropy = - 1 * log(0.68) = 0.167
From the above example, we can observe that all the three value for which the actual probabilities was equal to zero becomes zero and the value of the cross entropy depends upon the predicted value for the class whose probability is one.
Example 2:
Actual Probabilities:
[0, 1, 0, 0]
Predicted Probabilities:
[0.12, 0.28, 0.34, 0.26]
Cross Entropy = - 1 * log(0.28) = 0.558
Example 3:
Actual Probabilities:
[0, 1, 0, 0]
Predicted Probabilities:
[0.05, 0.80, 0.09, 0.06]
Cross Entropy = - 1 * log(0.80) = 0.096
One may say that all three examples are more or less the same but no there is a subtle difference between all three which is comparable in that as the predicted probability is close to the actual probability the value of the cross entropy decreases but as the predicted probability deviates from the actual probability value of the cross entropy function shoots up.
What is Binary Cross Entropy?
We have learned about the multiclass classification which is when there are more than two classes for which we are predicting probabilities. And hence as the name suggests it is a special case of the multiclass classification when the number of classes is only two so, there is a need to predict only probability for one class and the other one will be 1 – probability predicted.
We can modify the formula for the binary cross entropy as well.
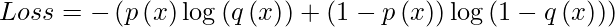
Categorical Cross-Entropy
The error in classification for the complete model is given by the mean of cross-entropy for the complete training dataset. This is the categorical cross-entropy. Categorical cross-entropy is used when the actual-value labels are one-hot encoded. This means that only one ‘bit’ of data is true at a time, like [1, 0, 0], [0, 1, 0], or [0, 0, 1]. The categorical cross-entropy can be mathematically represented as:
Sparse Categorical Cross-Entropy
In sparse categorical cross-entropy, truth labels are labeled with integral values. For example, if a 3-class problem is taken into consideration, the labels would be encoded as [1], [2], [3]. Note that binary cross-entropy cost functions, categorical cross-entropy, and sparse categorical cross-entropy are provided with the Keras API.
Share your thoughts in the comments
Please Login to comment...