Multi-Layer Perceptron Learning in Tensorflow
Last Updated :
05 Nov, 2021
In this article, we will understand the concept of a multi-layer perceptron and its implementation in Python using the TensorFlow library.
Multi-layer Perceptron
Multi-layer perception is also known as MLP. It is fully connected dense layers, which transform any input dimension to the desired dimension. A multi-layer perception is a neural network that has multiple layers. To create a neural network we combine neurons together so that the outputs of some neurons are inputs of other neurons.
A gentle introduction to neural networks and TensorFlow can be found here:
A multi-layer perceptron has one input layer and for each input, there is one neuron(or node), it has one output layer with a single node for each output and it can have any number of hidden layers and each hidden layer can have any number of nodes. A schematic diagram of a Multi-Layer Perceptron (MLP) is depicted below.
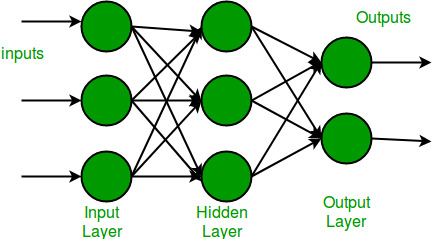
In the multi-layer perceptron diagram above, we can see that there are three inputs and thus three input nodes and the hidden layer has three nodes. The output layer gives two outputs, therefore there are two output nodes. The nodes in the input layer take input and forward it for further process, in the diagram above the nodes in the input layer forwards their output to each of the three nodes in the hidden layer, and in the same way, the hidden layer processes the information and passes it to the output layer.
Every node in the multi-layer perception uses a sigmoid activation function. The sigmoid activation function takes real values as input and converts them to numbers between 0 and 1 using the sigmoid formula.
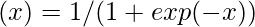
Now that we are done with the theory part of multi-layer perception, let’s go ahead and implement some code in python using the TensorFlow library.
Stepwise Implementation
Step 1: Import the necessary libraries.
Python3
import tensorflow as tf
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Activation
import matplotlib.pyplot as plt
|
Step 2: Download the dataset.
TensorFlow allows us to read the MNIST dataset and we can load it directly in the program as a train and test dataset.
Python3
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
|
Output:
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] – 2s 0us/step
Step 3: Now we will convert the pixels into floating-point values.
Python3
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
gray_scale = 255
x_train /= gray_scale
x_test /= gray_scale
|
We are converting the pixel values into floating-point values to make the predictions. Changing the numbers into grayscale values will be beneficial as the values become small and the computation becomes easier and faster. As the pixel values range from 0 to 256, apart from 0 the range is 255. So dividing all the values by 255 will convert it to range from 0 to 1
Step 4: Understand the structure of the dataset
Python3
print("Feature matrix:", x_train.shape)
print("Target matrix:", x_test.shape)
print("Feature matrix:", y_train.shape)
print("Target matrix:", y_test.shape)
|
Output:
Feature matrix: (60000, 28, 28)
Target matrix: (10000, 28, 28)
Feature matrix: (60000,)
Target matrix: (10000,)
Thus we get that we have 60,000 records in the training dataset and 10,000 records in the test dataset and Every image in the dataset is of the size 28×28.
Step 5: Visualize the data.
Python3
fig, ax = plt.subplots(10, 10)
k = 0
for i in range(10):
for j in range(10):
ax[i][j].imshow(x_train[k].reshape(28, 28),
aspect='auto')
k += 1
plt.show()
|
Output

Step 6: Form the Input, hidden, and output layers.
Python3
model = Sequential([
Flatten(input_shape=(28, 28)),
Dense(256, activation='sigmoid'),
Dense(128, activation='sigmoid'),
Dense(10, activation='sigmoid'),
])
|
Some important points to note:
- The Sequential model allows us to create models layer-by-layer as we need in a multi-layer perceptron and is limited to single-input, single-output stacks of layers.
- Flatten flattens the input provided without affecting the batch size. For example, If inputs are shaped (batch_size,) without a feature axis, then flattening adds an extra channel dimension and output shape is (batch_size, 1).
- Activation is for using the sigmoid activation function.
- The first two Dense layers are used to make a fully connected model and are the hidden layers.
- The last Dense layer is the output layer which contains 10 neurons that decide which category the image belongs to.
Step 7: Compile the model.
Python
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
|
Compile function is used here that involves the use of loss, optimizers, and metrics. Here loss function used is sparse_categorical_crossentropy, optimizer used is adam.
Step 8: Fit the model.
Python3
model.fit(x_train, y_train, epochs=10,
batch_size=2000,
validation_split=0.2)
|
Output:

Some important points to note:
- Epochs tell us the number of times the model will be trained in forwarding and backward passes.
- Batch Size represents the number of samples, If it’s unspecified, batch_size will default to 32.
- Validation Split is a float value between 0 and 1. The model will set apart this fraction of the training data to evaluate the loss and any model metrics at the end of each epoch. (The model will not be trained on this data)
Step 9: Find Accuracy of the model.
Python3
results = model.evaluate(x_test, y_test, verbose = 0)
print('test loss, test acc:', results)
|
Output:
test loss, test acc: [0.27210235595703125, 0.9223999977111816]
We got the accuracy of our model 92% by using model.evaluate() on the test samples.
Share your thoughts in the comments
Please Login to comment...