Integration is the calculation of an integral which is used in maths for finding many useful quantities such as areas, volumes, displacement, etc., that occur due to a collection of small data which cannot be measured singularly. Integrals are denoted using ” ∫ “.

Integration Notation
The concept of integration is used to solve two types of problems given below :
- When the derivatives are given, find the problem function,
- Find the area which is bounded by the graph of a function under some particular constraints.
These two problems lead to the development of the concept called the “Integral Calculus”, which consist of two types of integrals as given below:
- Definite Integral: An integral that includes the upper and lower limits is known as a definite integral. Definite Integral is also known as Riemann Integral. A definite Integral is represented as:
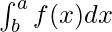
- Indefinite Integral: Indefinite integrals do not have upper and lower limits. It is represented as:
∫f(x)dx = F(x) + C
Here C is a constant and f(x) is a function that is known as integrand.
There are five types of integration methods available:
- Integration by substitution
- Integration by parts rule
- Integration by partial fraction
- Integration using trigonometric identities
- Integration of some particular function
Here, we only discuss integration by parts.
Integration by parts
Integration by parts is a method of integration that is often used for integrating the products of two functions. This technique is used to find the integrals by reducing them into standard forms. The following formula is used to perform integration by part:
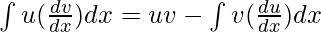
Where:
u is the first function of x: u(x)
v is the second function of x: v(x)
The formula of integration by parts with limits:
![Rendered by QuickLaTeX.com \int_{a}^{b} u(\frac{dv}{dx})dx = [uv]_{a}^{b} - \int_{a}^{b} v(\frac{du}{dx})dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63378e9dd46cc077cdaa47c8ffcc57d5_l3.png)
Where:
a is the lower limit
b is the upper limit
Derivation of Integration By Parts Formula:
Suppose u and w are any two differentiable functions of a single variable y.
As we already know how to differentiate a product,
y = uw
then, by the product rule of differentiation
dy/dx = d⁄dx(uw) = u d/dx(w) + w d/dx(u)
Rearranging this, we get
u d/dx(w) = d⁄dx(uw) – w d/dx(u)
or
uw’ = d⁄dx(wu) – wu’
On integrating both sides w.r.t x, we get
∫(uw’)dx = ∫d/dx(uw) dx – ∫(wu’)dx
The first term on the right simplifies, since
we are simply integrating what has been differentiated.
Therefore,
∫(uw’)dx = uw – ∫(u’w) dx
Now put
w’ = v
w = ∫v
Substituting the above values, we get
∫(uv)dx = u(∫vdx) – ∫(u’∫vdx)dx
Rules of integration by parts :
- Choose the first function as u and the second function as dv/dx.
- Differentiate u: u’
- Integrate dv/dx: (∫(dv/dx)dx = v)
- Put u, u’, v and ∫(dv/dx)dx into: u(∫vdx) −∫(u’ ∫vdx) dx
- Simplify and solve
ILATE Rule
In Integration by parts, generally, we use the preference order for deciding the first function, using ILATE Rule (Inverse trigonometric functions, logarithmic functions, algebraic functions, trigonometric functions, exponential functions). This rule states that the inverse trigonometric function should be assumed as the first function while performing the integration. Hence, the functions are to be assumed in order from left to right, by considering the left term (of ILATE) as the first function and the second term (of ILATE) as the second function, depending on the type of function involved. So, ILATE is the order in which we select the first function.

Below are the following steps for function u, where
I = Inverse trigonometric functions
such as sin-1 (x), cos-1 (x), tan-1 (x)
L = Logarithmic functions
such as ln(x), log(x)
A = Algebraic functions
such as x2, x3
T = Trigonometric functions
such as sin(x), cos(x), tan(x)
E = Exponential functions
such as ex, 3x
Sample Problem
Question 1. Evaluate ∫2x cos(x)dx
Solution:
Given that, ∫2x cos(x)dx
According to the rule of integration by parts,
Let us consider,
u = 2x and dv/dx = cos(x)
Then
du/dx = 2 and v = ∫cos(x) = sin(x)
Now, using the formula for integration by parts;
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
We get,
∫2x cox(x)dx = 2x sin(x) – ∫sinx.2dx
∫2x cos(x)dx = 2x sin(x) + 2cos(x) + c
where c is a constant.
Question 2. Evaluate ∫3x ln|x| dx
Solution:
Given, ∫3xln|x| dx
According to rule of integration by parts,
Let us consider,
u = ln|x| and dv/dx = 3x
Then
du/dx = 1/x and v = ∫3xdx = 3x2/2
Now, using the formula for integration by parts,
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
∫3x ln|x|dx = ln|x|.3x2/2 – ∫3x2/2(1/x)dx
= 3x2/2(ln|x|) – ∫3x/2 dx
= 3x2/2(ln|x|) – 3x2/4 + C
where C is a constant.
Question 3. Evaluate ∫10x2
Solution:
Given that, ∫10x2
According to rule of integration by parts,
Let us consider,
u = 10x2 and dv/dx = 1
Then
du/dx = 20x and v = ∫(1)dx = x
Now, using the formula for integration by parts;
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
∫10x2 dx = 10x2x – ∫x(20x)dx
∫10x2 dx = 10x3 – ∫20x2dx
∫10x2 dx = 10x3 – 20/3x3 + C
∫10x2 dx = 10x3/3 + C
where C is a constant.
Question 4. Evaluate ∫x2 e4x dx
Solution:
Given that, ∫x2 e4x dx
According to rule of integration by parts,
Let us consider,
u = x2 and dv/dx = e4x
Then
du/dx = 2x and v = ∫e4x dx = 1/4(e4x)
Then, using the formula for integration by parts,
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
∫x2e4x dx = (x2)1/4(e4x) – ∫1/4(e4x)(2x)dx
= 1/4(x2)(e4x) – ∫2/4(x)(e4x)dx
= 1/4(x2)(e4x) – ∫1/2(x)(e4x)dx
The resulting integral is still a product of
two functions i.e. 1/2(x) and e4x.
So, We use the formula for integration again.
This time we take
u = 1/2(x) and dv/dx = e4x
So
du/dx = 1/2 and v = ∫e4xdx = 1/4(e4x)
Now, on putting these values in above equation,
∫x2e4x dx = 1/4(x2)(e4x) – ∫2/4(x)(e4x)dx
= 1/4(x2e4x) – {2/4(x).1/4(e4x) – ∫(1/4(e4x).2/4 dx}
= 1/4(x2e4x) – 1/8(xe3x) + 1/8(e4x) + C
where C is a constant.
Question 5. Evaluate ∫ 2ex sin(x) dx
Solution:
Given that, ∫ 2exsin(x) dx
According to rule of integration by parts,
Let us consider,
u = 2ex and dv/dx = sin(x)
Then
du/dx = 2ex and v = ∫sin(x)dx = -cos(x)
Now, using the formula for integration by parts,
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
∫ 2exsin(x) dx = (2ex)(-cos(x)) – ∫(-cos(x))(2ex)dx
= -(2ex)cos(x) + ∫ 2ex cos(x)dx
The resulting integral is yet a product of two
functions i.e. 2ex and cos(x).
So, we use the formula for integration again.
This time we take
u = 2ex and dv/dx = cos(x)
So
du/dx = 2ex and v = ∫cos(x)dx = sin(x)
Now, on putting these values in the above equation, we get
∫ 2exsin(x) dx = -cos(x)(2ex) + ∫ 2ex cos(x)dx
= -(2ex)cos(x) + {2exsin(x) – ∫sin(x)(2ex)dx}
= -2excos(x) + 2exsin(x) – ∫2exsin(x)dx
Now, notice that the integral ∫exsin(x)dx in the result
is same as the integral in the given question.
So, let us assume this as I.
Therefore,
I = ∫ 2exsin(x) dx
So,
I = 2exsin(x) – 2excos(x) – I
2I = 2exsin(x) – 2excos(x)
2I = 2(exsin(x) – excos(x))
I = (exsin(x) – excos(x))
So,
∫ 2exsin(x) dx = exsin(x) – excos(x) + C
where C is a constant.
Question 6. Evaluate ∫2tan-1x dx
Solution:
Given, ∫2tan-1x dx
According to the rule of integration by parts,
Let us consider,
u = tan-1x and dv/dx = 2
Then
du/dx = 1/(1 + x2) and v = ∫(2)dx = 2x
Now, using the formula for integration by parts,
∫u(dv/dx)dx = uv – ∫v(du/dx)dx
∫2tan-1x dx = tan-1x(2x) – ∫2x(1/(1+x2))dx
let, p = (1 + x2)
So, dp/dx = 2x
⇒ x = 1/2
Now, substituting the above values, we get
∫tan-1x dx = tan-1x(2x) – ∫(1/p)dx
= 2xtan-1x – ∫(1/p)dx
= 2xtan-1x – lnp
= 2xtan-1x – ln(1 + x2)
= 2xtan-1x – ln√(1 + x2) + C
where C is a constant.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...