How to find the Fourier Transform of an image using OpenCV Python?
Last Updated :
03 Jan, 2023
The Fourier Transform is a mathematical tool used to decompose a signal into its frequency components. In the case of image processing, the Fourier Transform can be used to analyze the frequency content of an image, which can be useful for tasks such as image filtering and feature extraction.
In this article, we will discuss how to find the Fourier Transform of an image using the OpenCV Python library. We will begin by explaining the basics of the Fourier Transform and its application in image processing, then we will move on to the steps involved in finding the Fourier Transform of an image using OpenCV.
Basics of the Fourier Transform
The Fourier Transform decomposes a signal into its frequency components by representing it as a sum of sinusoidal functions. For a signal represented as a function of time, t, the Fourier Transform is given by the following equation:
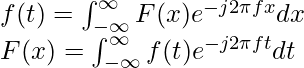
Where 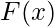 is the Fourier Transform of the signal f(t), and f is the frequency in Hertz (Hz). The Fourier Transform can be thought of as a representation of the signal in the frequency domain, rather than the time domain.
is the Fourier Transform of the signal f(t), and f is the frequency in Hertz (Hz). The Fourier Transform can be thought of as a representation of the signal in the frequency domain, rather than the time domain.
In the case of image processing, the Fourier Transform can be used to analyze the frequency content of an image. This can be useful for tasks such as image filtering, where we want to remove certain frequency components from the image, or feature extraction, where we want to identify certain frequency patterns in the image.
Steps to find the Fourier Transform of an image using OpenCV
Step 1: Load the image using the cv2.imread() function. This function takes in the path to the image file as an argument and returns the image as a NumPy array.
Step 2: Convert the image to grayscale using the cv2.cvtColor() function. This is optional, but it is generally easier to work with grayscale images when performing image processing tasks.
Step 3: Use the cv2.dft() function to compute the discrete Fourier Transform of the image. This function takes in the image as an argument and returns the Fourier Transform as a NumPy array.
Step 4: Shift the zero-frequency component of the Fourier Transform to the center of the array using the numpy.fft.fftshift() function. This step is necessary because the cv2.dft() function returns the Fourier Transform with the zero-frequency component at the top-left corner of the array.
Step 5: Compute the magnitude of the Fourier Transform using the numpy.abs() function. This step is optional, but it is generally easier to visualize the frequency content of an image by looking at the magnitude of the Fourier Transform rather than the complex values.
Step 6: Scale the magnitude of the Fourier Transform using the cv2.normalize() function. This step is also optional, but it can be useful for improving the contrast of the resulting image.
Step 7: Use the cv2.imshow() function to display the magnitude of the Fourier Transform.
Example 1
Here is the complete example of finding the Fourier Transform of an image using OpenCV:
Input Image :

Input Image
Python3
import cv2
import numpy as np
image = cv2.imread(r"Dhoni-dive_165121_730x419-m.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
fourier = cv2.dft(np.float32(gray), flags=cv2.DFT_COMPLEX_OUTPUT)
fourier_shift = np.fft.fftshift(fourier)
magnitude = 20*np.log(cv2.magnitude(fourier_shift[:,:,0],fourier_shift[:,:,1]))
magnitude = cv2.normalize(magnitude, None, 0, 255, cv2.NORM_MINMAX, cv2.CV_8UC1)
cv2.imshow('Fourier Transform', magnitude)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
Output image:
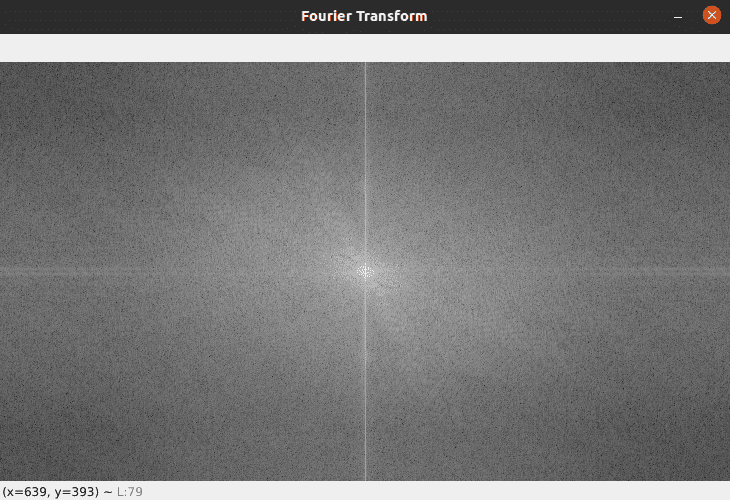
Fourier transform
In this example, we first load the image and convert it to grayscale using the cv2.imread() and cv2.cvtColor() functions. Then, we compute the discrete Fourier Transform of the image using the cv2.dft() function and store the result in the ‘fourier’ variable.
Example 2
In this program, we find the discrete Fourier transform of the input image. We find and plot the magnitude spectrum.
Input Image :

Input Image
Python3
import numpy as np
import cv2
from matplotlib import pyplot as plt
image_path = r"Dhoni-dive_165121_730x419-m.jpg"
image = cv2.imread(image_path, 0)
DFT = cv2.dft(np.float32(image), flags=cv2.DFT_COMPLEX_OUTPUT)
shift = np.fft.fftshift(DFT)
row, col = image.shape
center_row, center_col = row // 2, col // 2
mask = np.zeros((row, col, 2), np.uint8)
mask[center_row - 30:center_row + 30, center_col - 30:center_col + 30] = 1
fft_shift = shift * mask
fft_ifft_shift = np.fft.ifftshift(fft_shift)
imageThen = cv2.idft(fft_ifft_shift)
imageThen = cv2.magnitude(imageThen[:,:,0], imageThen[:,:,1])
plt.figure(figsize=(10,10))
plt.subplot(121), plt.imshow(image, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(imageThen, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
|
Output image:

Discrete Fourier transform
Share your thoughts in the comments
Please Login to comment...