How to calculate Variance?
Last Updated :
04 Oct, 2023
What is Variance?
Variance is another measure of dispersion and is based on standard deviation. The term variance was first used by R.A. Fisher in 1913 and means the square of the standard deviation of the given distribution. Symbolically, Variance is denoted by σ2.
Variance = σ2
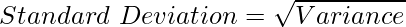
A bigger value of variance means the distribution has more variability or less consistency, and vice-versa.
Standard Deviation and Variance are two measures of dispersion and are closely related to each other. The only difference between them is that Standard Deviation is the square root of Variance; however, Variance is the average squared deviation from the mean.
1. Actual Mean Method:
Example:
Determine the variance of the following distribution using the Actual Mean Method.
Solution:
Arithmetic Mean 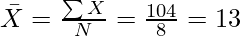
Standard Deviation 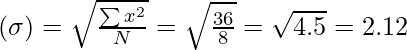
Variance = 2.122 = 4.5
Variance = 4.5
2. Assumed Mean Method:
Example:
Calculate the variance of the data given below using Assumed Mean Method.
Solution:
Standard Deviation 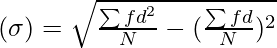
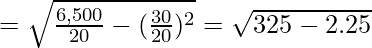
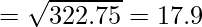
Variance = 17.92 = 322.75
Variance = 322.75
3. Step-Deviation Method:
Example:
Calculate the Variance of the data given below using the Step-Deviation Method.
Solution:
Standard Deviation (\sigma)=\sqrt{\frac{\sum{fd^\prime{^2}}}{N}-(\frac{\sum{fd^\prime}}{N})^2}\times{C}
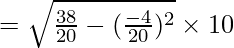
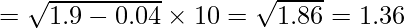
Variance = 1.362 = 1.86
Variance = 1.86
Share your thoughts in the comments
Please Login to comment...