Poisson Distribution : Meaning, Characteristics, Shape, Mean and Variance

What is Poisson Distribution?

Poisson distribution describes the likelihood of a certain number of events occurring within a given time frame. It applies to situations where events happen independently and at a constant average rate. This distribution proves useful when numerous trials exist, each with a minimal chance of success. In layman’s language, it helps in forecasting how often something occurs over a specific time, provided we know the average rate of occurrence. Under Poisson Distribution,

• The probability of success in the interval is very small and is unstable.
• The occurrence of success in an interval is statistically independent of that in any other trial.

If X has a Poisson Distribution with parameter 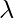, then we can write X ~ Poi().

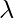Probability Distribution Function (PDF) of Poisson Distribution

The Probability Density Function (PDF) of a Poisson distribution helps in determining the chance of a certain number of events happening within a set time or space. It is handy when events are infrequent and happen independently. For instance, imagine a bakery. Customers arrive randomly at an average rate of 4 customers per hour. We can apply the Poisson distribution to calculate the probability of a specific number of customers arriving in one hour. The PDF of Poisson Distribution can be written as:

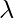P(X = x) = , x = 1, 2, 3,……..; >0

Where,

• P(x) represents the probability of a specific number of events occurring.
• e is the mathematical constant approximately equal to 2.7183.
• λ is the average rate of event occurrences in the given time or space.

Characteristics of Poisson Distribution

The Poisson distribution is used for events that are rare, independent, and where the number of events in a given time or space is small. Given below are some important characteristics of the Poisson distribution:

• Events are separate and don’t influence each other.
• Only one event can happen at a particular moment.
• It is used when there are many trials or attempts.
• The average (mean) number of events equals the variance (spread) in the distribution and is denoted by .
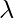• When you multiply the number of trials (n) by the probability of success (p), it equals 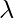, which is a constant.
• The standard deviation is always the square root of the mean (μ).
• If the average number of events is large, the Poisson distribution behaves like a normal distribution.

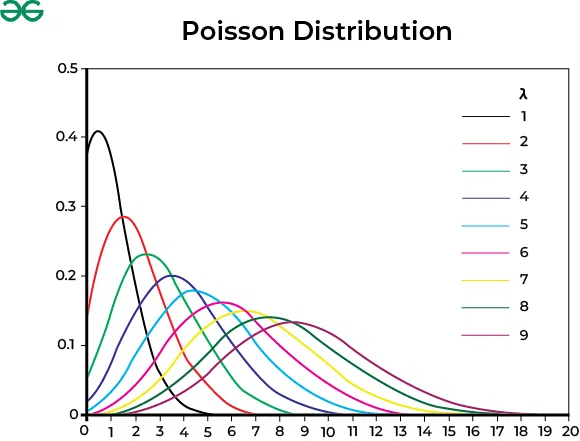
Shape of Poisson Distribution

A poison distribution is positively skewed. However, the degree of skewness decreases with an increase in the value of .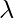

Mean and Variance of Poisson Distribution

In the Poisson distribution, the mean and variance of the distribution are the same because this distribution is characterised by a property where the average rate of event occurrences (λ) is also equal to the spread or variability in the distribution. This property is specific to the Poisson distribution and is a key feature of it. Therefore, The expected mean E(X) and the variance V(X) are both equal to λ.

E(X) = V(X) =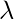 

or

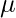= ² =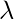 

Fitting a Poisson Distribution

Fitting a Poisson Distribution involves finding the best match between observed data and the Poisson model. It is like searching for a hat that fits just right. Suppose, there is data on how often something happens, like the number of customers arriving at a store each hour. If this data follows a pattern where events are rare and occur independently, the Poisson distribution might be a good fit. To fit it, one compares the actual data to what the Poisson model predicts. If they match up well, it suggests that the Poisson distribution accurately describes the situation. In practical terms, fitting a Poisson Distribution helps in understanding and making predictions about situations involving rare events, like customer arrivals or machine failures. It is a bit like finding the right puzzle piece that fits snugly into the data available.

Example:

A sample of 200 similar firms in a big industrial town revealed the following distribution of fatal accidents in a year. Fit a Poisson distribution corresponding to it.

No. of Accidents	0	1	2	3	4	5
No. of Firms	91	69	33	4	2	1

Solution:

No. of Accidents (x)	No. of Firms (f)	fx	P(x)	Expected Frequencies P(x)×200
0	91	0	0.4493	89.9
1	69	69	0.3595	71.9
2	33	66	0.1438	28.7
3	4	12	0.0383	7.66
4	2	8	0.0077	1.54
5	1	5	0.0012	0.24
Total	200	160		199.94 ~ 200

*Mean () =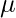 

Poisson Distribution as an Approximation to Binomial Distribution

The Poisson distribution simplifies the Binomial distribution. The Binomial distribution deals with the number of successes in a set of trials. However, when there are many trials with a small chance of success, it becomes impractical to calculate using the Binomial probabilities. In such situations, the Poisson distribution works as a shortcut. It focuses on the frequency of events in a specific span of time or space, especially for rare occurrences.

For instance, imagine a bustling city intersection where accidents are infrequent. Computing the probability of exactly 2 accidents in a day with the Binomial distribution would be complex due to the large number of cars and low accident probability per car. In this case, employing the Poisson distribution as an estimate simplifies the process. By adjusting the parameters to match the average (λ = 0.1), we can readily determine the probability of exactly 2 accidents in a day using the Poisson distribution formula.

Example:

In a manufacturing process, there is a 2% defective rate for a certain product. If a sample of 200 products is selected, what is the probability that exactly 5 of them are defective, using the Poisson distribution as an approximation to the Binomial distribution?

Solution:

According to the given information, the probability of success (defective product) is p = 0.02 (2% defective rate), and the number of trials is n = 200. Using the formula for the average rate of occurrence in a Poisson distribution 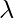= np, we can calculate .

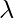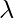= np = 200 × 0.02 = 4

Now, we can use the Poisson distribution formula to find the probability of exactly 5 defective products x = 5,

Calculate the individual components:

e^-4 ≈ 0.0183

4⁵ = 1024

5! = 120

Substitute these values into the formula:

P(X=5) = 0.15616

∴ the probability of exactly 5 defective products in a sample of 200, using the Poisson distribution as an approximation to the Binomial distribution, is approximately 0.15.

Examples of Poisson Distribution

Example 1:

In a call centre, calls are received at an average rate of 10 calls per hour. What is the probability of receiving exactly 15 calls in an hour? Use the Poisson distribution formula.

Solution:

According to the given information, the average rate (λ) is 10 calls per hour. We have to determine exactly 15 calls in an hour; P (X = 15)

Now, putting the values in the formula of Poisson Distribution

Here e = 2.7183

P(X = 15) = 0.0347

Example 2:

A bakery sells an average of 5 croissants per hour. What is the probability that they sell no croissants in the next 20 minutes?

Solution:

According to the given information:

The average rate (λ) is 5 croissants per hour.

Time is 20 minutes or 1/3 of 60 minutes.

∴ λ = 5 × 1/3 = 5/3

We have to determine the probability of selling 0 croissants in the next 20 minutes; i.e., P (X = 0).

Now, putting the values in the formula of Poisson Distribution

P(X=0) = 0.1888