Heptacontagon Number
Last Updated :
23 Jun, 2021
Given a number N, the task is to find Nth Heptacontagon number.
A Heptacontagon number is class of figurate number. It has 70 – sided polygon called heptacontagon. The N-th heptacontagon number count’s the 70 number of dots and all others dots are surrounding with a common sharing corner and make a pattern. The first few heptacontagonol numbers are 1, 70, 207, 412 …
Examples:
Input: N = 2
Output: 70
Explanation:
The second heptacontagonol number is 70.
Input: N = 3
Output: 207
Approach: The N-th heptacontagon number is given by the formula:
- Nth term of s sided polygon =
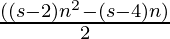
- Therefore Nth term of 70 sided polygon is
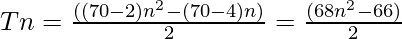
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int heptacontagonNum(int n)
{
return (68 * n * n - 66 * n) / 2;
}
int main()
{
int N = 3;
cout << "3rd heptacontagon Number is = "
<< heptacontagonNum(N);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
int heptacontagonNum(int n)
{
return (68 * n * n - 66 * n) / 2;
}
int main()
{
int N = 3;
printf("3rd heptacontagon Number is = %d",
heptacontagonNum(N));
return 0;
}
|
Java
class GFG{
static int heptacontagonNum(int n)
{
return (68 * n * n - 66 * n) / 2;
}
public static void main(String[] args)
{
int N = 3;
System.out.println("3rd heptacontagon Number is = " +
heptacontagonNum(N));
}
}
|
Python3
def heptacontagonNum(n):
return (68 * n * n - 66 * n) // 2;
N = 3;
print("3rd heptacontagon Number is =",
heptacontagonNum(N));
|
C#
using System;
class GFG{
static int heptacontagonNum(int n)
{
return (68 * n * n - 66 * n) / 2;
}
public static void Main()
{
int N = 3;
Console.Write("3rd heptacontagon Number is = " +
heptacontagonNum(N));
}
}
|
Javascript
<script>
function heptacontagonNum(n)
{
return (68 * n * n - 66 * n) / 2;
}
var N = 3;
document.write("3rd heptacontagon Number is = " + heptacontagonNum(N));
</script>
|
Output: 3rd heptacontagon Number is = 207
Time Complexity: O(1)
Auxiliary Space: O(1)
Reference: https://en.wikipedia.org/wiki/Heptacontagon
Share your thoughts in the comments
Please Login to comment...