Icositrigonal Number
Last Updated :
17 Mar, 2021
Given a number N, the task is to find Nth Icositrigonal number or not.
An Icositrigonal number is class of figurate number. It has 23 – sided polygon called Icositrigon. The N-th Icositrigonal number count’s the 23 number of dots and all others dots are surrounding with a common sharing corner and make a pattern. The first few Icositrigonol numbers are 1, 23, 66, 130, 215, 321, 448 …
Examples:
Input: N = 2
Output: 23
Explanation:
The second Icositrigonol number is 66.
Input: N = 6
Output: 321
Approach: The N-th Icositrigonal number is given by the formula:
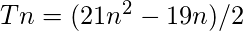
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int Icositrigonal_num(int n)
{
return (21 * n * n - 19 * n) / 2;
}
int main()
{
int n = 3;
cout << Icositrigonal_num(n) << endl;
n = 10;
cout << Icositrigonal_num(n);
return 0;
}
|
Java
class GFG{
static int IcositrigonalNum(int n)
{
return (21 * n * n - 19 * n) / 2;
}
public static void main(String[] args)
{
int n = 3;
System.out.print(IcositrigonalNum(n) + "\n");
n = 10;
System.out.print(IcositrigonalNum(n));
}
}
|
Python3
def IcositrigonalNum(n):
return (21 * n * n - 19 * n) / 2;
n = 3
print(IcositrigonalNum(n))
n = 10
print(IcositrigonalNum(n))
|
C#
using System;
class GFG{
static int IcositrigonalNum(int n)
{
return (21 * n * n - 19 * n) / 2;
}
public static void Main()
{
int n = 3;
Console.WriteLine(IcositrigonalNum(n));
n = 10;
Console.WriteLine(IcositrigonalNum(n));
}
}
|
Javascript
<script>
function Icositrigonal_num(n)
{
return (21 * n * n - 19 * n) / 2;
}
let n = 3;
document.write(Icositrigonal_num(n) + "</br>");
n = 10;
document.write(Icositrigonal_num(n));
</script>
|
Reference: https://en.wikipedia.org/wiki/Polygonal_number
Share your thoughts in the comments
Please Login to comment...