Second heptagonal numbers
Last Updated :
07 Apr, 2021
The Second heptagonal numbers series can be represented as
4, 13, 27, 46, 70, 99, 133, 172, 216, …..
Nth term
Given an integer N. The task is to find the N-th term of the given series.
Examples:
Input: N = 1
Output: 4
Input: N = 4
Output: 46
Approach: The idea is to find the general term for the Second heptagonal numbers. Below is the computation of the general term for second heptagonal numbers:
Series = 4, 13, 27, 46, 70, 99, 133, 172, 216, …..
Difference = 13-4, 27-13, 46-27, 70-46, …………….
Difference = 9, 14, 19, 24……which is a AP
So nth term of given series
nth term = 4 + (9 + 14 + 19 + 24 …… (n-1)terms)
nth term = 4 + (n-1)/2*(2*9+(n-1-1)*5)
nth term = 4 + (n-1)/2*(18+5n-10)
nth term = 4 + (n-1)*(5n+8)/2
nth term = n*(5*n+3)/2
Therefore, the Nth term of the series is given as
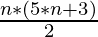
Below is the implementation of above approach:
C++
#include <iostream>
#include <math.h>
using namespace std;
void findNthTerm(int n)
{
cout << n * (5 * n + 3) / 2
<< endl;
}
int main()
{
int N = 4;
findNthTerm(N);
return 0;
}
|
Java
class GFG{
static void findNthTerm(int n)
{
System.out.println(n * (5 * n + 3) / 2);
}
public static void main(String[] args)
{
int N = 4;
findNthTerm(N);
}
}
|
Python 3
def findNthTerm(n):
print(n * (5 * n + 3) // 2)
N = 4
findNthTerm(N)
|
C#
using System;
class GFG{
static void findNthTerm(int n)
{
Console.Write(n * (5 * n + 3) / 2);
}
public static void Main()
{
int N = 4;
findNthTerm(N);
}
}
|
Javascript
<script>
function findNthTerm(n)
{
document.write(parseInt((n * (5 * n + 3)) / 2));
}
let N = 4;
findNthTerm(N);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Reference:OEIS
Share your thoughts in the comments
Please Login to comment...