Find the value of P and modular inverse of Q modulo 998244353
Last Updated :
07 Jan, 2024
Given two integer P and Q, the task is to find the value of P and modular inverse of Q modulo 998244353. That is
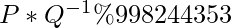
Note: P and Q are co-prime integers
Examples:
Input: P = 1, Q = 4
Output: 748683265
Explanation:
Refer below for the explanation of the example.
Input: P = 1, Q = 16
Output: 935854081
Approach: The key observation in the problem is that Q is co-prime with the 998244353, Then Q-1 always exists which can be computed using Extended euclidean Algorithm
For Example:
For P = 1 and Q = 4
We know that,
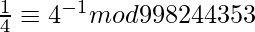
That is, 4 * 748683265 = 2994733060 equivalent to 1 mod 998244353
Therefore, 1*4^(-1) = 748683265
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
long long calculate(long long p,
long long q)
{
long long mod = 998244353, expo;
expo = mod - 2;
while (expo) {
if (expo & 1) {
p = (p * q) % mod;
}
q = (q * q) % mod;
expo >>= 1;
}
return p;
}
int main()
{
int p = 1, q = 4;
cout << calculate(p, q) << '\n';
return 0;
}
|
Java
import java.util.*;
class GFG{
static long calculate(long p, long q)
{
long mod = 998244353, expo;
expo = mod - 2;
while (expo != 0)
{
if ((expo & 1) == 1)
{
p = (p * q) % mod;
}
q = (q * q) % mod;
expo >>= 1;
}
return p;
}
public static void main(String[] args)
{
long p = 1, q = 4;
System.out.println(calculate(p, q));
}
}
|
Python3
def calculate(p, q):
mod = 998244353
expo = 0
expo = mod - 2
while (expo):
if (expo & 1):
p = (p * q) % mod
q = (q * q) % mod
expo >>= 1
return p
if __name__ == '__main__':
p = 1
q = 4
print(calculate(p, q))
|
C#
using System;
class GFG{
static long calculate(long p, long q)
{
long mod = 998244353, expo;
expo = mod - 2;
while (expo != 0)
{
if ((expo & 1) == 1)
{
p = (p * q) % mod;
}
q = (q * q) % mod;
expo >>= 1;
}
return p;
}
public static void Main(string[] args)
{
long p = 1, q = 4;
Console.WriteLine(calculate(p, q));
}
}
|
Javascript
<script>
function calculate(P, Q)
{
let mod = 998244353, expo;
expo = mod - 2;
p = 748683265;
while (expo != 0)
{
if ((expo & 1) == 1)
{
P = (P * Q) % mod;
}
Q = (Q * Q) % mod;
expo >>= 1;
}
return p;
}
let p = 1, q = 4;
document.write(calculate(p, q));
</script>
|
Time Complexity: O(log(expo)), where the expo is calculated in the program
Auxiliary Space: O(1), as no extra space is used
Share your thoughts in the comments
Please Login to comment...