An equation in maths is a statement that equates two terms involving variables and constants. Equations are a form of statement that shows the balance and relation between two expressions. To, understand this concept of Equation more clearly, there are various types of equations – Linear, Quadratic, Polynomial, Logarithmic, Trigonometric as well as some other shape equations like equations of Line, Circle, Ellipse, Parabola, etc.
Not only does this article talk about different equations but also systems of equations, both linear and non-linear, providing techniques for effective solutions, along with methods to solve equations, be they linear, quadratic, polynomial, exponential, or trigonometric.
Furthermore, this article tells about real-world applications of these mathematical equations, at the end some practice problems have been offered to learners.

What Is an Equation?
An equation is a mathematical statement that shows the equality between two mathematical expressions. An equation contains variables (letters), numbers, mathematical symbols, and operations. An equation shows two parts that are separated by an equal sign (=), where the left-hand side is called LHS and the right-hand side is called RHS. The equation tells us that LHS equals RHS.
Equation Definition
In the simplest way, an Equation can be defined as “A mathematical sentence that shows the two expressions are equal”.
For Example, 2(x+y) = 2x+ 2y, this equation says that the LHS is 2(x+y) is equivalent to the RHS is 2x + 2y.
Types of Equations
Mathematics uses a range of equations that solve different purposes and show the connection between quantities and situations. Some key equation types in mathematics include linear equations, quadratic equations, polynomial equations, logarithmic equations, exponential equations, and trigonometric equations. Let’s delve into each of them to gain a better understanding.

Linear Equations
The linear equation contains a constant, variable, or product of a constant and shows the relationship where the variables have a constant rate of change. Linear equations can be represented on a single-line graph.
The general form of a linear equation is:
Ax + By = C
Where A, B, and C are constants, with A and B are not equal to zero.
Example of Linear Equation
Linear Equation in One Variable: 2x + 10 = 0
Linear equation in Two Variables: 2x + 3y – 10 = 0
Quadratic Equations
In a quadratic equation, a variable gets raised to the power of 2, making a U-shaped curve when graphed.
A quadratic equation can be written as:
Ax2+ Bx + C = 0
Where A, B and C are constant and A ≠ 0.
Example of Quadratic Equation
2x2 + 3x – 10 = 0
Where, A = 2, B = 3, C = -10.
Some other examples include:
- 2x2 – 3x + 1 = 0
- 5x2 + 10x + 2 = 0
- -3x2 – 6x – 9 = 0
- x2 – 2x + 1 = 0
- 3x2 = 12x
Polynomial Equations
A polynomial equation is a mathematical expression that includes variables, exponents (such as squares and cubes), and coefficients (numbers). The degree of the equation depends on the highest exponent present. When the highest exponent (or power) of any variable is 2, then a quadratic equation will be formed.
On the other hand, a polynomial function is a mathematical expression that includes one variable raised to various powers and may appear multiple times in an equation, such as x and x².
The general form of the polynomial equation is given as:
anxn + a(n-1)x(n-1) + ……+ a1x + a0 = 0
Where,
- an, a(n-1),….., a1, a0 are coefficients.
- x is a variable.
- n is a whole number that can’t be negative and shows the highest degree of the polynomial.
Logarithmic Equations
Logarithmic equations use logarithmic functions, which are the reverse of exponential functions. In other words, these equations help us solve for the unknown variable that is found as an exponent in an exponential expression.
The general form of a logarithmic equation is:
y = logb(x)
Where,
- log represents the logarithm.
- x is the number which needs to find.
- b is the base of the logarithm, and a positive number which is greater than 1.
- y is the result or exponent to which the base b must be raised to get x.
In other words, this equation reads as “the logarithm base b of x equals y”.
Exponential Equations
An exponential equation is a maths equation that uses an exponential function. This type of equation can be written as:
f(x) = ax
In the equation, x is a variable and a is a real number which is referred to as the base of the function, with a being greater than 0. The exponential function represents repeated multiplication or growth at a consistent percentage rate. Typically, the most widely utilized base for exponential functions is , which is an approximately equal value of 2.71828.
The general form of an exponential equation is:
f(x) = a.ekx
Where,
- f(x) represents the value of the function at a given x
- a is the initial value or the function’s value at x = 0.
- e is the base of natural logarithms (approximately 2.71828).
- k is a constant that determines the rate of growth or decay.
- x is the variable, which can take different values.
Trigonometric Equations
Trigonometry deals with equations that involve trigonometric ratios like sine, cosine, tangent, cotangent, secant, and cosecant. These equations relate the angles and side lengths in triangles. For example, the equation sinθ = 0.5 represents a trigonometric equation.
Let’s consider a right-angled triangle with ∠ an acute angle.
The following trigonometry ratios can be derived:
- Sin θ = Opposite side / Hypotenuse = BC / AB
- Cos θ = Adjacent side / Hypotenuse = AC / AB
- Tan θ = Opposite side / Adjacent side = BC / AC = Sinθ / Cosθ
- Cosec θ = Hypotenuse / Opposite side = AB/BC = 1 / Sinθ
- Sec θ = hypotenuse / Adjacent side = AB / AC = 1 / Cosθ
- Cot θ = Adjacent side / opposite side = AC / BC = 1 / Tanθ
These trigonometry ratios can be calculated at different angles. Given below is the Table for trigonometry ratio values at different angles.
|
| 0 | ½
| 1/√2 | √3/2 | 1 |
| 1 | √3 / 2
| 1/√2 | ½ | 0 |
| 0 | 1/√3
| 1 | √3 | ∞ |
| ∞ | 2 | √2 | 2/√3 | 1 |
| 1 | 2/√3 | √2 | 2 | ∞ |
| ∞ | √3 | 1 | 1/√3 | 0 |
Read More about Trigonometric Table.
Some Special Equations
Apart from the equations that are just discussed above, there are some special equations as well, which can be called as equations of shapes, that are discussed further.
Equation of a Line
The general form of the equation of a line in two variables and first degree is Ax+By+C=0
A, B, and C are constant real numbers and a graphical representation of the line equation will give a straight line
The equation of a line in slope intercept form can be written as:
y = mx+c
Where ‘m’ is the slope of the line and ‘c’ is the intercept of y.
The general equation of line can be written in slope intercept form as:
- y = (-A/B)x – (C/B)
- m = (-A/B)
- c = (C/B)
“The intercept is the point through which the line crosse x-axis and y-axis”
Equation of Circle
The general equation of a circle is x² + y²+ 2gx + 2fy + c = 0 , where g, f and c are constants. This form allows us to represent circles with centers not necessarily at the origin and can represent circles with various characteristics. The values of g,f and c determine the center, radius, and other properties of the circle.
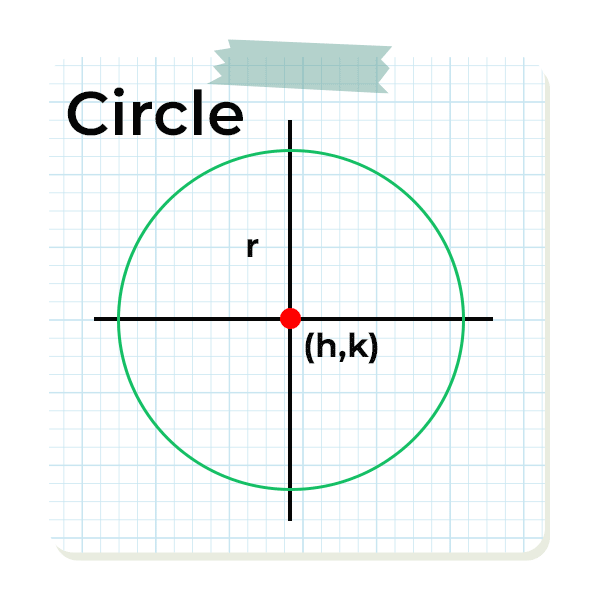
- Equation of a Circle with Center at Origin
When the center of a circle is at the origin (0, 0), then the equation will be: x²+y²= r² , where r is the radius of the circle. This equation represents a circle with center at the origin with a radius of r.
- Equation of a Circle with Center Not at Origin
To express the equation of a circle with center (h,k) and radius r: (x-h)²+(y-k)² = r². In this equation, the values (h,k) represent the coordinates of the center, while r represents the radius of the circle. Essentially, this equation defines a circle centered at (h,k) with a radius equal to r.
Equation of Parabola
A parabola is a curve that looks the same on both sides and has three important parts, namely, the focus, directrix, and axis of symmetry. The focus is in the middle on the axis of symmetry, while the directrix is a parallel line. The parabola is consist of points where the distance from the focus is the same as the distance from the directrix and the sharpest point on the parabola is called the vertex.
A parabola is a curved shape that looks like a “U” and can open either upwards or downwards if it’s vertical, or leftwards or rightwards if it’s horizontal. The equation of the parabola determines its orientation and shape, with ‘a’ determining how wide or narrow parabola is, and (h,k) representing the vertex – the point where the curve changes direction.
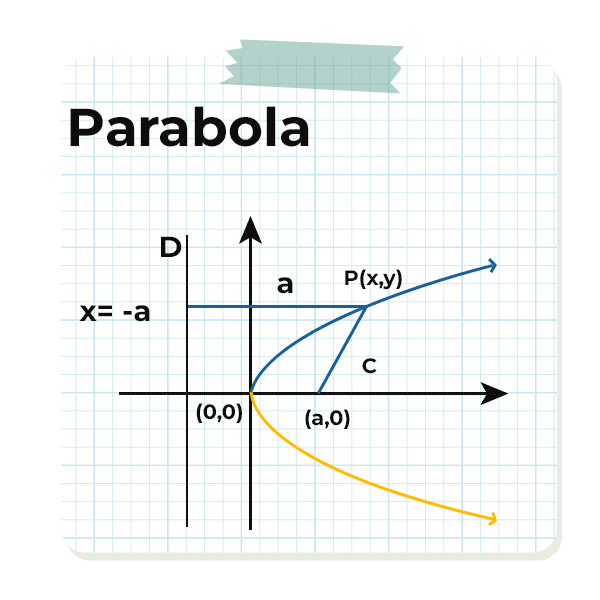
The general equation of a parabola is given as:
- Standard Equation for a Regular Parabola
y2 = 4ax
y = a(x-h)2+ k
where h,k represents the vertex.
x = a(y-k)2+ h
where h,k represents the vertex.
Equation of Ellipse
An ellipse can be defined as the set of points where the sum of the distances from any point on the shape to two fixed points (known as foci) remains constant.
A circle is also an ellipse with it’s foci at the same point. Ellipse can be defined by it’s two axis x-axis and y-axis called as mazor axis and minor axis.
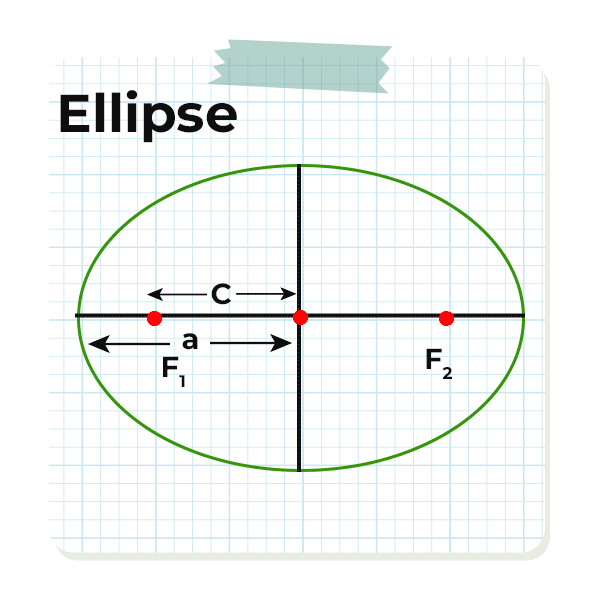
The general form of ellipse equation is:
(x-h)2/a2 + (y-k)2/b2 = 1
Where,
- (h, k) are the coordinates of the center of the ellipse.
- The semi-major axis, denoted as ‘a’ represents the distance from the center of an ellipse to its furthest point along the major axis.
- The semi-minor axis, marked as ‘b’, refers to the distance from the center of the ellipse to its farthest point along the minor axis.
Equation of Hyperbola
A hyperbola belongs to a group of curves called conic sections. The equation that describes a hyperbola depends on its orientation and the location of its center.
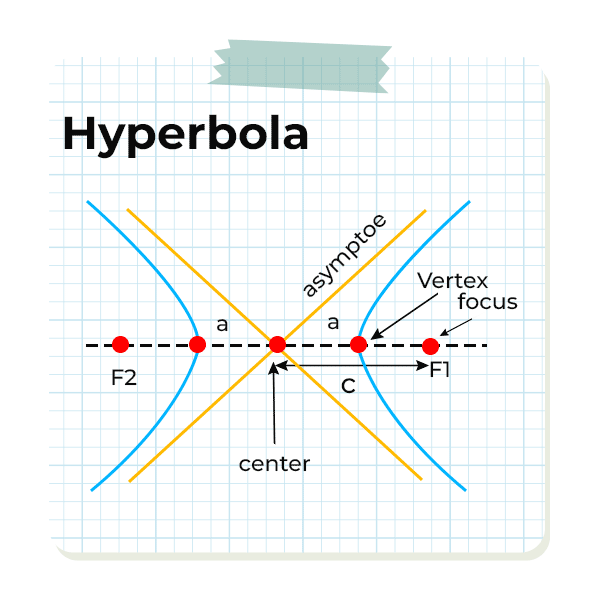
Here are the standard form equations for hyperbolas:
For a horizontal hyperbola with its center at the point (h, k), a horizontal major axis, and a vertical minor axis, the equation is as follows:
(x-h)2/a2 – (y-k)2/b2 = 1
Where,
- (h, k) is the the middle of the hyperbola.
- a shows how far it is from the middle to a point on the longer line.
- b shows how far it is from the middle to a point on the shorter line.
The equation for a vertical hyperbola with its center at the point (h, k), a vertical major axis, and a horizontal minor axis can be expressed as:
(y-k)2/a2 – (x-h)2/b2 = 1
Where,
- (h, k) is the center of the hyperbola.
- a shows distance from the center to a vertex along the longer side.
- b shows distance from the center to a vertex along the shorter side.
In both equations, if the term with x is subtracted from the term with y, it represents a hyperbola that opens horizontally, and if the term with y is subtracted from the term with x, it represents a hyperbola that opens vertically.
Hyperbolas are unique curves that have two branches curving away from each other. As they move away from the center, they approach two dashed lines known as asymptotes.
Equation in Calculus
There are two branches of Calculus namely, differential calculus and integral calculus which deals with finding derivative and antiderivative of a function respectively. The equation in differential and integral calculus are discussed below:
Differential Equation
A differential equation involves terms and derivatives of a variable (dependent) with respect to another (independent). For instance, dy/dx = f(x), where x is independent and y is dependent. It represents a rate of change and describes how one quantity changes in relation to another. Various formulas exist for solving these equations.
The order of a differential equation is determined by the highest derivative present. For example, dy/dx = 7x + 8 is a first-order equation, while (d²y/dx²) + 2(dy/dx) + y = 0 is a second-order one. First-order equations involve only the first derivative, like dy/dx, while second-order equations include the second derivative, like d²y/dx².
The degree of a differential equation is the highest power of the derivative it contains. It’s determined by looking at the derivatives in the equation. For example, if an equation has a second derivative like (d²y/dx²), it’s a first-degree equation. Some equations may not have a defined degree if they don’t fit a polynomial pattern.
Integral Equations
Integration is like adding up specific pieces descrete data. It’s used to find functions that describe area, displacement, or volume, which are made up of many small pieces that can’t be measured separately.
In math, calculus uses a concept called “limits” to get accurrate answer. Limits are a way to look at what happens to the points on a graph as they come closer until the distance between two points are equal to zero.
In calculus there are two branches:
- Differential Calculus (dealing with changes)
- Integral Calculus (dealing with additions)
There are basically two problems where intergration is used:
- To find the original function when we have its rate of change.
- To figure out the area under a function’s graph within specific rules..
Integral Calculus: Integral calculus is all about these two problems. It has two parts: definite (specific area) and indefinite (finding the original function). The Fundamental Theorem of Calculus connects differentiation and integration.
Definite Integral: An integral that contains the upper and lower limits then it is a definite integral. On a real line, x is restricted to lie. Riemann Integral is the other name of the Definite Integral. A definite Integral is represented as
[Tex]\int_a^bf(x)dx = F(b) – F(a)
[/Tex]
Where,
F is the antiderivative of ‘f’ {dF(x)/dx = f(x)}
Indefinite Integral: An indefinite integral doesn’t have these upper and lower limits. It’s written like this:
∫f(x)dx = F(x) + C
In this equation, C is any constant, and f(x) is the function we’re integrating, also known as the integrand. It means finding the function that, when you take its derivative, gives you f(x).
Systems of Equations
Systems of equations are mathematical expressions that involve multiple variables. The goal is to find values for these variables that satisfy all the given equations at the same time. There are different methods to solve system of linear equations, such as substitution, elimination, and graphical representation. The outcomes can include a single solution, no solution when lines are parallel, or an infinite number of solutions when lines coincide. These methods can also be applied to non-linear equations to solve more complex systems.
System of Linear Equations
A system of linear equations is a set of two or more equations in which the variables have exponents of 1 and are related linearly, meaning they form straight lines when graphed. The goal is to find values of the variables that satisfy all the equations in the system simultaneously.
System of Non-Linear Equations
A system of non-linear equations consists of two or more equations where the relationships between variables are not linear. These relationships involve variables raised to powers other than 1, such as squares, cubes, or other nonlinear functions. Solving these systems can be more complex compared to linear systems because nonlinear equations can produce curves instead of straight lines when graphed.
Example of System of Non-Linear Equations
- Equation 1: x2 + y = 8
- Equation 2: xy + 2 = 0
In this system, x and y are the variables, and the equations involve nonlinear terms, such as x² and xy. Solving such systems typically requires advanced techniques and may not always have analytical solutions.
How to Solve Systems of Equations?
There are 3 ways of solving systems of equations- Graphical method, substitution method and elimination method
Substitution Method
The substitution method involves solving one equation for one variable and then substituting that expression into the other equation. This reduces the system to a single equation with one variable, which can be solved.
- Equation (1): 2x + 3y = 8
- Equation (2): 3x -2y = 4
To solve a pair of equations using substitution, first solve one of the equations for one of the variables. Then substitute the result for that variable in the other equation.
Step 1: Solve any one equation for x
2x+3y=8
⇒ 2x =-3y+8 …….(subtracting both sides by 3)
⇒ x = ½ (-3y+8) ………(dividing both sides by 2)
⇒ x = -3/2y+4 ……… equation (3)
Step 2: Substitute the value of x that we just got in the other equation 3x – 2y = 4
3 [(-3/2)y+ 4] – 2y= 4
⇒ (-9/2)y + 12 – 2y= 4
⇒ (-13/2)y + 12 = 4 ……….(adding the coefficients of y)
⇒ (-13/2)y= -8 ………..(subtracting 12 from both sides)
⇒ y = 16/13 (dividing both sides by -13/2 or multiplying by the reciprocal of this fraction -2/13)
Step 3: Substitute this value of y in equation (3)
x= -3/4 × [16/13 + 4]
⇒ x = -24/13 +4
⇒ x= 28/13
Now the system is solved and we have value of x and y as
x = 28/13 and y= 16/13
Graphical Method
The graphical method involves graphing each equation on the same coordinate plane and finding the point(s) where the graphs intersect. These points represent the solutions to the system of equations.
For the given
- Equation (1): x + 2y=8
- Equation (2): 3x – 2y=4
Plot both the equations on the graph, the point where both the equations intersect is the solution. Putting the values of x and y we can find that the graph of two lines intersect at (3, 5/2) which is the required solution of the graph.
Learn More, Graph of Linear Equations in Two Variables
Elimination Method
The elimination method involves adding or subtracting equations to eliminate one variable. This creates a new equation with only one variable, which can be solved.
Taking the same equation to solve using elimination method
- Equation (1) : 2x + 3y = 8
- Equation (2) : 3x – 2y = 4
Step 1: To make the coefficients of variable x in both equations equal, multiply equation (1) by 3 and equation (2) by 2. The equation formed are
6x + 9y = 24
⇒ 6x – 4y = 8
Step 2: Subtract like terms in equation (2) from equation (1)
6x – 6x + 9y + 4y = 24 – 8
⇒ 13y = 16
⇒ y = 16/13
Step 3: Put the value of y in equation (2)
3x – 2(16/13) = 4
⇒ 3x – (32/13) = 4
⇒ 3x = 4+ (32/13)
⇒ 3x = 84/13
⇒ x = 28/13
Hence, the value of x and y are
x = 28/13 and y= 16/13
Solving Equations
Solving equations involves finding the values that make a given equation true. There are various techniques for solving different types of equations, such as linear, quadratic, polynomial, exponential, and trigonometric equations. Each type of equation requires its own specific method or function to find the solutions, providing a range of versatile methods for tackling mathematical problems.
Solving Linear Equations
Example: Check if 5 = 2x +3
Solution:
Put x = 1
5 = 2(1) + 3
⇒ 5 = 2+3
⇒ 5 = 5
LHS = RHS
Solving Quadratic Equations
There are various ways of solving a quadratic equation- factor method, completing squares method and quadratic formula.
The quadratic formula to find variable x in a quadratic equation ax2 + bx + c = 0 can be written as:
[Tex]x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}
[/Tex]
Let us solve a quadratic equation x2-3x=28 using the quadratic formula
Step 1: convert the given equation into the standard quadratic equation ax2+bx+c=0
x2– 3x – 28=0
Here, a = 1, b = -3, c = -28
Step 2: Put the values of a,b, and c in the quadratic formula
[Tex]\frac{-\left(-3\right)\pm\sqrt{\left(-3\right)^2-4\left(-28\right)}}{2}
[/Tex]
[Tex]\Rightarrow \frac{-\left(-3\right)\pm\sqrt{9-4\left(-28\right)}}{2}
[/Tex]………..(solving [-32])
[Tex]\Rightarrow \frac{-\left(-3\right)\pm\sqrt{9+112}}{2}
[/Tex]………….(multiplying -4 by -28)
[Tex]\Rightarrow \frac{-\left(-3\right)\pm\sqrt{121}}{2}
[/Tex]…………..(adding values in root)
[Tex]\Rightarrow \frac{-\left(-3\right)\pm11}{2}
[/Tex]…………(solving root)
[Tex]\Rightarrow \frac{\left(3\right)\pm11}{2}
[/Tex]……….. ( – multiplying with minus is plus)
Now solve the equation [Tex]x=\frac{\left(3\right)\pm11}{2}
[/Tex]when ± is plus. Add 3 to 11.
x= 14/2
⇒ x = 7
Now solve the equation [Tex]x=\frac{\left(3\right)\pm11}{2}
[/Tex]when ± is minus. Subtract 11 from 3.
x =(-28)
⇒ x =(-4)
Hence x = 7, -4
Solving Polynomial Equations
There are various ways of solving a polynomial equation based on its complexity. The main methods to solve a polynomial equations are:
Roots of a Polynomial: A root of a polynomial is a value of x that makes polynomial equivalent to zero, i.e, P(x)=0
Factorization and Division: To find the roots of a mathematical expression, the common technique used is called factorization of polynomial. This method involves breaking down a complex expression into simpler components that are more easy to solve. For instance, if there is an equation like x²-4, by dividing the equation into (x-2)(x+2) and then solve for x by equating each part to zero: x-2=0 and x+2=0 . The values of x that make each component zero correspond to the roots of the equation.
Complex Roots: Some polynomials, such as x²+1 , do not have real number roots. However, by considering complex numbers, every non-constant polynomial has at least one root. This is known as the fundamental theorem of algebra.
Solving Exponential Equations
Exponential Equations looks complex which requires basic algebra knowledge. In mathematics there are mainly three types of exponential equations to solve and hence there are three methods to solve them, namely:
- Equations with Exponents having Same Base
Let’s take an equation 102+x = 103 to understand more clearly.
In this equation 10 is the base on both side which is common. So, to solve this equation ignore the base and solve for x.
2+x=3
⇒ 2-2+x = 3-2……….(substracting 2 from both sides)
⇒ x=1
Now, put this value of x in the original equation
102+x = 103
⇒ 103 = 103
Hence solved.
- Equations with Exponents and Whole Numbers
Suppose, 2x+5 – 2 = 14
In this equation there are whole numbers on both the side.
∴ solve the whole numbers
2x+5 -2+2 = 14+2 ………… (adding 2 on both sides)
⇒ 2x+5 = 16
Covert 16 into an exponent with the base 2
⇒ 2×2×2×2 = 16
∴ 24 = 16
Put 24 in place of 16
2x+5 = 24
Now that the base are same, so ignore base and solve for x
x + 5 = 4
⇒ x = (-1)
Put the value of x in the original equation
2(-1)+5 – 2 = 14
⇒ 24 – 2 = 14
⇒ 16-2 = 14
⇒ 14 = 14
Hence, solved.
- Using Log terms without Same Base
In the equation 2x = 4y, (2 and 4) are the base, which are not same.
To find the value of x and y , multiply the equation on both side with natural logarithm (In)
ln(2x ) = ln(4y )
Using the Power rule of logarithm, we will get
x ln(2) = y ln(4)
Solve for y in terms of x
y = xln(2)/ln(4)
this gives us a relationship between x and y
Solving Trigonometric Equations
Trigonometric equations contain expressions with trigonometric functions such as sine, cosine, and tangent. To find the solutions for a variable x within the range 0 ≤ x ≤ 2π, we identify the principal solutions. If these solutions incorporate an integer ‘n,’ they are known as general solutions.
The table below shows the general trigonometric equations with their general solutions.
|
| θ = nπ |
| θ = nπ + 2/π |
| θ = nπ |
| θ = (2nπ + π/2) = (4n + 1) π/2 |
| θ = 2nπ |
| θ = nπ ± (-1)2 α, where α ϵ [-π/2, π/2] |
| θ = 2nπ ± α, where α ϵ [0,π] |
| θ = nπ ± α, where α ϵ [-π/2, π/2] |
| θ = nπ ± α |
| θ = nπ ± α |
| θ = nπ ± α |
Algebraic Equation
An Algebraic equation is a form of equation that consistes of variables, coefficients and constants. Algebraic equation can be represented as P = 0
Where, P is a polynomial.
According to P=0, it can be said that, an algebraic equation has polynomial on onne side and is set equal to zero. For example, in algebraic equation x-10 = 0,
x-10 is a polynomial and it is set qual to zero.
An algebraic equation is suppose to have balance on booth side to avoid any error, which means if there is any change on LHS side there will be equal chnge on RHS side as well.
To understand through an equation, consider an equation 2+2 = 4, this equation is balanced on both side , but if 5 is added on LHS side the equation will become 2+2+5 = 4, which is not correct. So, in order to make it balances 5 is supposed to be add on RHS side.
2+2+5 = 4+5.
This same will apply on multiplication, division, subtraction or any opertion that can be used
From the various types of algebraic equations, few of them are:
- Polynomial Equations
- Quadratic Equations
- Cubic Equations
- Rational polynomial Equations
- Trigonometric Equations
Algebraic Equation Formulas
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b)(a – b) = a2 – b2
- (x + a)(x + b) = x2 + x(a + b) + ab
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a – b)3 = a3 – 3a2b + 3ab2 – b3
- a3 + b3 = (a + b)(a2 – ab + b2)
- a3 – b3 = (a – b)(a2 + ab + b2)
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
- Quadratic Formula: x = [-b ± √(b² – 4ac)]/2a
Parts of Algebraic Equation
There are different parts of equation. Let’s break an equation say, 2x+5 = 11
- Variables: x is a variable with unknown value that is supposed to be find. a variable can be any lettter not just x.
- Coefficients: The numbers attached with the variable, in this case 2, is the coefficient of x. it tells how many times a variable is multiplied..
- Constants: Numbers in the equation which have no attached variable with it are the constants of equation, in this case 5 and 11 are the constants.
- Operators: The symbols that perform mathematical operations (+, -,\ ) are the operators of the equation. In this equation, the plus sign (+) is the operator used for addition.
- Equal Sign: It separates the two sides of the equation. Whatever is on the left side should be equal to what’s on the right side.
Algebraic Expression vs. Equation
The difference between Algebraic Expression and Equation are tabulated below:
|
Combination of numbers, variables, and operations.
| Mathematical statement showing equality between two values.
|
Does not contain an equal sign (=).
| Contains an equal sign (=) indicating equality.
|
3x + 2y is an algebraic expression.
| 3x + 2y = 10 is an algebraic equation.
|
Describes a mathematical relationship without asserting equality.
| Asserts equality between two mathematical expressions.
|
Doesn’t require balancing as there’s no equality assertion.
| Requires balancing both sides to maintain equality.
|
Doesn’t have a specific solution, as there’s no equality to satisfy.
| Has a solution, which is the value(s) that satisfy the equation.
|
Application of Equations
The applications of Equations are mentioned below:
- Equations serve as tools to describe diverse aspects of the natural world, encompassing everything from the movement of objects to the principles governing electricity and even the intricate realm of quantum mechanics.
- Engineers play a vital role in various fields, using their expertise to design structures, electrical circuits, and mechanical systems.
- Mathematical equations have practical uses in economics as they help model economic trends, analyze supply-demand relationships, and study the dynamics of financial markets.
- In chemistry, equations are essential for balancing chemical reactions, determining the structure of molecules, and studying chemical processes.
- Financial professionals use equations to calculate interest rates, investment returns, and to assess and manage financial risks.
- Equations form the foundation of algorithms in computer science, enabling tasks such as data analysis and encryption.
- Environmental scientists use equations to model climate change, predict pollution dispersion, and study ecosystems.
- Astronomy benefits from equations, which help explain the movements of celestial bodies, planetary orbits, and various cosmic phenomena.
- In the field of medicine, equations are applied in medical imaging, determining drug dosages, and modeling the spread of diseases.
- Equations play a crucial role in statistical analysis, hypothesis testing, and interpreting research results and provide the necessary framework to carry out tasks such as data analysis accurately.
- Machine learning algorithms depends on mathematical equations as the foundation for their operations. These equations allow computers to learn from data and make accurate predictions based on that information.
- Architects and civil engineers use equations to guide architectural design, perform structural analysis, and address acoustics in buildings.
- Equations play a role in education by shaping curriculum development and assessing educational outcomes.
- Telecommunications experts use equations to govern signal processing, optimize network performance, and ensure efficient data transmission.
Solved Examples on Equations
Example 1: 3x + 4 = 10
Solution:
In the given equation subtract 4 from both sides
3x + 4 – 4 = 10 – 4
3x = 6
x = 6/3 …… ( dividing both sieds by 3)
x = 2
On putting the value of x in the equation given:
3(2) + 4 = 10
6 + 4 = 10
∴ 10 = 10
Example 2: x2 – 5x + 6 = 0
Solution:
In the given equation:
a = 1, b = (-5), c = 6
Using the quadratic formula to solve for x:
[Tex]x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
[/Tex]
Put he values of a,b, and c in the formula , we get:
[Tex]x=\frac{-\left(-5\right)\pm\sqrt{\left(-5\right)^2-4\left(1\right)\left(6\right)}}{2\left(1\right)}
[/Tex]
⇒ [Tex]x=\frac{-\left(-5\right)\pm\sqrt{25-24}}{2}
[/Tex]
⇒ [Tex]x=\frac{5\pm\sqrt{1}}{2}
[/Tex]
On simplifying
x = (5±1)/2
Calculating x with ‘+’ and ‘-‘ both
x1 = (5+1)/2
⇒ x1 =6/2
⇒ x1 = 3
Thus, x2 = (5-1)/2
⇒ x2 = 4/2
⇒ x2 = 2
∴ The solutions to the quadratic equation are x = 3 and x = 2
Example 3: 3x – 2(2x + 1) = 5
Solution:
First simplify the equation
3x – 4x – 2 = 5
⇒ 3x – 4x – 2 – 5 = 5 – 5 …… (subract 5 from both sides)
Solve the like terms
– x – 7 = 0
⇒ – x- 7 + 7 = 0+7 …… (adding 7 on both sides)
⇒ – x = 7 …… ( multiply both sides by -1 to make x positive)
∴ x = -7
Example 4: log(x) = 2
Solution:
Write logarithmic equation in exponential form
NOTE: When not specified take common logarithm as 10
log(x) = 2
⇒ 102 = x
⇒ 102 = 100
⇒ x = 100
Example 5: 2(2x+1) = 16
Solution:
convert the equation with same base
2(2x+1) = 24 ….. (eq 1.)
Solve the exponents first:
⇒ 2x+1 = 4
⇒ 2x + 1 – 1 = 4 – 1 …… (subracting 1 from both sides)
⇒ 2x = 3
⇒ x = 3/2 …… (dividing both sides by 2)
put he value of x in eq 1.
2(2 . [3/2] + 1) = 24
⇒ 2(3+1) = 24
⇒ 24 = 24
Practice Problems on Equations
Q1. Solve for x in the exponential equation: 2x = 16
Q2. Factor the polynomial equation: x3-8x2+16x = 0
Q3. Tina is saving money for a new bicycle. She currently has ₹80 saved up and plans to save an additional amount each week. After 7 weeks, she wants to have ₹220 in total. What is the amount Tina plans to save each week?
Q4. Solve this quadratic equation: 2x2 -5x+3=0
Q5. A population of bacteria doubles every hour. If there are initially 100 bacteria, how many will there be after 5 hours?
Q6. John and Sarah are buying apples and oranges. John buys 4 apples and 3 oranges for ₹6. Sarah buys 2 apples and 5 oranges for ₹5. What is the cost of one apple and one orange?
FAQs on Equations in Maths
1. How can I solve a System of Equations?
To solve a system of equations, there are various methods one can use, such as substitution, elimination, or graphing. These techniques helps in determining the values for variables that satisfy all the equations at once.
2. What is Algebraic Equation?
An algebraic equation is a mathematical statement that demonstrates the equality between two expressions. This equation usually includes variables, constants, and various mathematical operations.
3. Is 20+3 an algebraic equation?
No, 20+3 is not an algebraic equation, but a mathematical expression which will result in numeric value 23.
4. What is the difference between an Equation and a Function?
In mathematics, an equation defines the relationship between two mathematical expressions, typically involving variables. On the other hand, a function is a specialized type of equation that links an input value to a single output value.
5. What is Linear Equation?
Linear Equation is a mathematical equation in which the power of the variable is one.
6. What are the different ways of Solving a Quadratic Equation?
Factorization, completing the square, or by using quadratic formula are the three methods of solving a quadratic equation.
7. What is the use of a Graphical Representation of an Equation?
Graphs are a valuable tool for understanding equations because they allow us to visualize the relationships between different variables. They can help us identify potential solutions and patterns or trends in data.
8. What is the Graph of a Quadratic Equation?
The graph of a Quadratic Equation is a Parabola in nature.
9. What is Foci and where can we find Foci in terms of Mathematics?
In conic sections, like ellipses and hyperbolas, foci (the plural of focus) play a vital role in describing the shapes and properties of these curves. These are fundamental in comprehending the geometry of these figures.
10. What is the Equation and Formula?
A mathematical statement that depicts equality, like 2x + 3 = 7 is called as equation, whereas, a formula is a specific type of equation that shows a mathematical relationship or rule, which is used to calculate a value. For example, the formula for the area of a rectangle is Area = length × width.
11. What is an Equation in Simple Form?
In simple terms equation is a mathematical statement which states the equality between two given situation (that are described in a form of mathematical expression).
12. What is Bernoulli’s Equation in Maths?
Bernoulli’s equation describes energy conservation in fluid flow. This equation connects pressure, velocity, and height in fluid systems and is vital in fluid dynamics and aerodynamics.
Share your thoughts in the comments
Please Login to comment...