Difference between Batch Gradient Descent and Stochastic Gradient Descent
Last Updated :
23 Apr, 2023
In order to train a Linear Regression model, we have to learn some model parameters such as feature weights and bias terms. An approach to do the same is Gradient Descent which is an iterative optimization algorithm capable of tweaking the model parameters by minimizing the cost function over the train data. It is a complete algorithm i.e it is guaranteed to find the global minimum (optimal solution) given there is enough time and the learning rate is not very high. Two Important variants of Gradient Descent which are widely used in Linear Regression as well as Neural networks are Batch Gradient Descent and Stochastic Gradient Descent(SGD).
Batch Gradient Descent: Batch Gradient Descent involves calculations over the full training set at each step as a result of which it is very slow on very large training data. Thus, it becomes very computationally expensive to do Batch GD. However, this is great for convex or relatively smooth error manifolds. Also, Batch GD scales well with the number of features.
Batch gradient descent and stochastic gradient descent are both optimization algorithms used to minimize the cost function in machine learning models, such as linear regression and neural networks. The main differences between the two are:
Data Processing Approach:
Batch gradient descent computes the gradient of the cost function with respect to the model parameters using the entire training dataset in each iteration. Stochastic gradient descent, on the other hand, computes the gradient using only a single training example or a small subset of examples in each iteration.
Convergence Speed:
Batch gradient descent takes longer to converge since it computes the gradient using the entire training dataset in each iteration. Stochastic gradient descent, on the other hand, can converge faster since it updates the model parameters after processing each example, which can lead to faster convergence.
Convergence Accuracy:
Batch gradient descent is more accurate since it computes the gradient using the entire training dataset. Stochastic gradient descent, on the other hand, can be less accurate since it computes the gradient using a subset of examples, which can introduce more noise and variance in the gradient estimate.
Computation and Memory Requirements:
Batch gradient descent requires more computation and memory since it needs to process the entire training dataset in each iteration. Stochastic gradient descent, on the other hand, requires less computation and memory since it only needs to process a single example or a small subset of examples in each iteration.
Optimization of Non-Convex Functions:
Stochastic gradient descent is more suitable for optimizing non-convex functions since it can escape local minima and find the global minimum. Batch gradient descent, on the other hand, can get stuck in local minima.
In summary, batch gradient descent is more accurate but slower, while stochastic gradient descent is faster but less accurate. The choice of algorithm depends on the specific problem, dataset, and computational resources available.
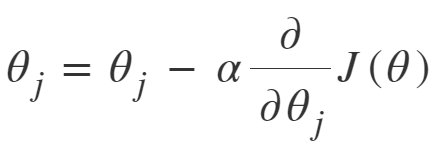
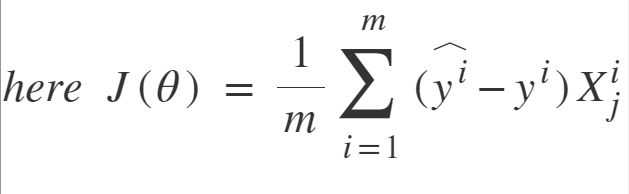 Stochastic Gradient Descent: SGD tries to solve the main problem in Batch Gradient descent which is the usage of whole training data to calculate gradients at each step. SGD is stochastic in nature i.e. it picks up a “random” instance of training data at each step and then computes the gradient, making it much faster as there is much fewer data to manipulate at a single time, unlike Batch GD.
Stochastic Gradient Descent: SGD tries to solve the main problem in Batch Gradient descent which is the usage of whole training data to calculate gradients at each step. SGD is stochastic in nature i.e. it picks up a “random” instance of training data at each step and then computes the gradient, making it much faster as there is much fewer data to manipulate at a single time, unlike Batch GD. 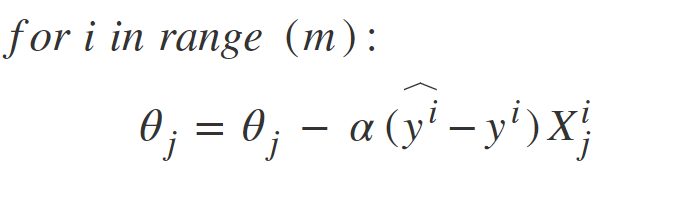 There is a downside of the Stochastic nature of SGD i.e. once it reaches close to the minimum value then it doesn’t settle down, instead bounces around which gives us a good value for model parameters but not optimal which can be solved by reducing the learning rate at each step which can reduce the bouncing and SGD might settle down at global minimum after some time.
There is a downside of the Stochastic nature of SGD i.e. once it reaches close to the minimum value then it doesn’t settle down, instead bounces around which gives us a good value for model parameters but not optimal which can be solved by reducing the learning rate at each step which can reduce the bouncing and SGD might settle down at global minimum after some time.
Difference between Batch Gradient Descent and Stochastic Gradient Descent
.math-table { border-collapse: collapse; width: 100%; } .math-table td { border: 1px solid #5fb962; text-align: left !important; padding: 8px; } .math-table th { border: 1px solid #5fb962; padding: 8px; } .math-table tr>th{ background-color: #c6ebd9; vertical-align: middle; } .math-table tr:nth-child(odd) { background-color: #ffffff; }
| Batch Gradient Descent |
Stochastic Gradient Descent |
| Computes gradient using the whole Training sample |
Computes gradient using a single Training sample |
| Slow and computationally expensive algorithm |
Faster and less computationally expensive than Batch GD |
| Not suggested for huge training samples. |
Can be used for large training samples. |
| Deterministic in nature. |
Stochastic in nature. |
| Gives optimal solution given sufficient time to converge. |
Gives good solution but not optimal. |
| No random shuffling of points are required. |
The data sample should be in a random order, and this is why we want to shuffle the training set for every epoch. |
| Can’t escape shallow local minima easily. |
SGD can escape shallow local minima more easily. |
| Convergence is slow. |
Reaches the convergence much faster. |
| It updates the model parameters only after processing the entire training set. |
It updates the parameters after each individual data point. |
| The learning rate is fixed and cannot be changed during training. |
The learning rate can be adjusted dynamically. |
| It typically converges to the global minimum for convex loss functions. |
It may converge to a local minimum or saddle point. |
| It may suffer from overfitting if the model is too complex for the dataset. |
It can help reduce overfitting by updating the model parameters more frequently. |
Share your thoughts in the comments
Please Login to comment...