Gradient Descent With RMSProp from Scratch

Gradient descent is an optimization algorithm used to find the set of parameters (coefficients) of a function that minimizes a cost function. This method iteratively adjusts the coefficients of the function until the cost reaches the local, or global, minimum. Gradient descent works by calculating the partial derivatives of the cost function with respect to each of the coefficients. The algorithm then makes small adjustments to the coefficients in order to reduce the cost until it reaches a minimum. The direction of the adjustments is determined by the negative of the gradient of the cost function. Optimizers are methods or algorithms that reduce a loss (an error) by adjusting various parameters and weights, minimizing the loss function, and thereby improving model accuracy and speed. One such optimization technique is RMSprop.

RMSProp (Root Mean Squared Propagation) is an adaptive learning rate optimization algorithm. It is an extension of the popular Adaptive Gradient Algorithm and is designed to dramatically reduce the amount of computational effort used in training neural networks. This algorithm works by exponentially decaying the learning rate every time the squared gradient is less than a certain threshold. This helps reduce the learning rate more quickly when the gradients become small. In this way, RMSProp is able to smoothly adjust the learning rate for each of the parameters in the network, providing a better performance than regular Gradient Descent alone.

The RMSprop algorithm utilizes exponentially weighted moving averages of squared gradients to update the parameters. Here is the mathematical equation for RMSprop:

1. Initialize parameters:
   • Learning rate: α
   • Exponential decay rate for averaging: γ
   • Small constant for numerical stability: ε
   • Initial parameter values: θ
2. Initialize accumulated gradients (Exponentially weighted average):
   • Accumulated squared gradient for each parameter: E_t​= 0
3. Repeat until convergence or maximum iterations:
   • Compute the gradient of the objective function with respect to the parameters:
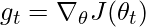
   • Update the exponentially weighted average of the squared gradients:
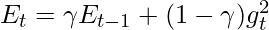
   • Update the parameters:

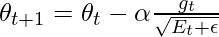
where,

• g_t is the gradient of the loss function with respect to the parameters at time t
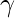• is a decay factor
• E_t​ is the exponentially weighted average of the squared gradients
• α is the learning rate
• ϵ is a small constant to prevent division by zero

This process is repeated for each parameter in the optimization problem, and it helps adjust the learning rate for each parameter based on the historical gradients. The exponential moving average allows the algorithm to give more importance to recent gradients and dampen the effect of older gradients, providing stability during optimization.

Implementation

Now, we will look into the implementation of the RMSprop. We will first import all the necessary libraries as follows.

Python3

# Importing libraries
import numpy as np
import matplotlib.pyplot as plt
from numpy import arange, meshgrid

Now, we will define our objective function and its derivatives. For this article we are considering the objective function to be 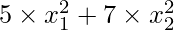where x₁ and x₂ are variables.

Python3

# Defining the objective function
def objective(x1, x2):
    # Replace with your objective function
    return 5 * x1**2.0 + 7 * x2**2.0

# Defining the derivative of the objective function w.r.t x1
def derivative_x1(x1, x2):
    # Replace with the derivative of your objective function w.r.t x1
    return 10.0 * x1

# Defining the derivative of the objective function w.r.t x2
def derivative_x2(x1, x2):
    # Replace with the derivative of your objective function w.r.t x2
    return 14.0 * x2

Now, let us visualize this equation. We will look into its 3D graph between x₁, x₂, and y and we will also look into its 2D representation (contour plot).

Python3

# Plotting the objective function in 3D and 2D

# Defining the range of x1 and x2
x1 = arange(-5.0, 5.0, 0.1)
x2 = arange(-5.0, 5.0, 0.1)

# Creating a meshgrid of x1 and x2
x1, x2 = meshgrid(x1, x2)

# Calculating the objective function for each combination of x1 and x2
y = objective(x1, x2)

# Plotting the objective function in 3D and 2D
fig = plt.figure(figsize=(12, 4))

# Plot 1 - 3D plot
ax = fig.add_subplot(1, 2, 1, projection='3d')
ax.plot_surface(x1, x2, y, cmap='viridis')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('y')
ax.set_title('3D plot of the objective function')

# Plot 2 - Contour plot (2D plot)
ax = fig.add_subplot(1, 2, 2)
ax.contour(x1, x2, y, cmap='viridis', levels=20)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('Contour plot of the objective function')

# Displaying the plots
plt.show()

Output:

Now, let us define our RMSprop optimizer.

Python3

# Defining the RMSprop optimizer
def rmsprop(x1, x2, derivative_x1, derivative_x2, learning_rate, gamma, epsilon, max_epochs):
    # Creating empty lists to store the trajectories of x1, x2, and y
    x1_trajectory = []
    x2_trajectory = []
    y_trajectory = []

    # Setting the initial values of x1, x2, and y
    x1_trajectory.append(x1)
    x2_trajectory.append(x2)
    y_trajectory.append(objective(x1, x2))

    # Defining the initial values of e1 and e2
    e1 = 0
    e2 = 0

    # Running the gradient descent loop
    for _ in range(max_epochs):
        # Calculating the derivatives of the objective function w.r.t x1 and x2
        gt_x1 = derivative_x1(x1, x2)
        gt_x2 = derivative_x2(x1, x2)

        # Calculating the exponentially weighted averages of the derivatives
        e1 = gamma * e1 + (1 - gamma) * gt_x1**2.0
        e2 = gamma * e2 + (1 - gamma) * gt_x2**2.0

        # Updating the values of x1 and x2
        x1 = x1 - learning_rate * gt_x1 / (np.sqrt(e1 + epsilon))
        x2 = x2 - learning_rate * gt_x2 / (np.sqrt(e2 + epsilon))

        # Appending the values of x1, x2, and y to their respective lists
        x1_trajectory.append(x1)
        x2_trajectory.append(x2)
        y_trajectory.append(objective(x1, x2))

    return x1_trajectory, x2_trajectory, y_trajectory

Now, let us optimize our objective function using the RMSprop function.

Python3

# Defining the initial values of x1, x2, and other hyperparameters
x1_initial = -4.0
x2_initial = 3.0
learning_rate = 0.1
gamma = 0.9
epsilon = 1e-8
max_epochs = 50

# Running the RMSprop algorithm
x1_trajectory, x2_trajectory, y_trajectory = rmsprop(
                                                x1_initial,
                                                x2_initial,
                                                derivative_x1,
                                                derivative_x2,
                                                learning_rate,
                                                gamma,
                                                epsilon,
                                                max_epochs
                                            )

# Printing the optimal values of x1, x2, and y
print('The optimal value of x1 is:', x1_trajectory[-1])
print('The optimal value of x2 is:', x2_trajectory[-1])
print('The optimal value of y is:', y_trajectory[-1])

Output:

The optimal value of x1 is: -0.10352260359924752
The optimal value of x2 is: 0.0025296212056016548
The optimal value of y is: 0.05362944016394148

Now, let us visualize the path or trajectory of the objective function.

Python3

# Displying the path of y in each iteration on the contour plot
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)

# Plotting the contour plot
ax.contour(x1, x2, y, cmap='viridis', levels=20)

# Plotting the trajectory of y in each iteration
ax.plot(x1_trajectory, x2_trajectory, '*',
        markersize=7,  color='dodgerblue')

# Setting the labels and title of the plot
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_title('RMSprop Optimization path for ' + str(max_epochs) + ' iterations')

# Displaying the plot
plt.show()

Output: