Descartes’ Circle Theorem with implementation
Last Updated :
23 Nov, 2022
In geometry, Descartes’ theorem states that for every four mutually tangent circles, the radii of the circles satisfy a certain quadratic equation. One can construct a fourth circle tangent to three given, mutually tangent circles.
Descartes’ Circle Theorem helps us to find the radius of a circle when there are 4 circles with positive integer radius r1, r2, r3 and r4 as shown in the figure below. It finds the radius r4 of the circle formed by three circles of radius r1, r2, r3 as shown in the image below.
(Note that the circles in the picture below are tangent to each other.)
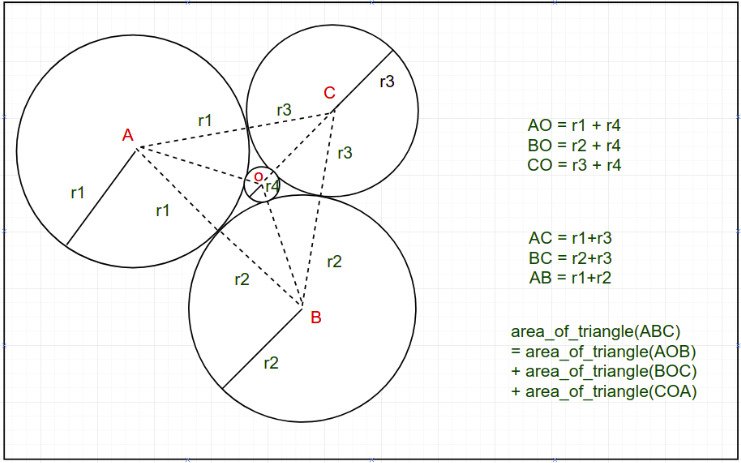
Examples:
Input: r1 = 1, r2 = 1, r3 = 1
Output: 0.154701
Input: r1 =23, r2 = 46, r3 = 69
Output: 6.000000
The theorem says that the reciprocals of radii, or “curvatures”, of these circles
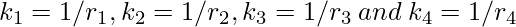
satisfies the following relation:
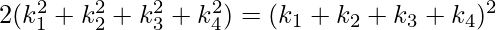
One of the circles can be enclosed among all the remaining three, as in the figure, in which case the corresponding curvature 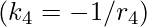 here is considered negative and the above relation still holds.
here is considered negative and the above relation still holds.
If 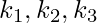 are known, one can solve for k4,
are known, one can solve for k4,
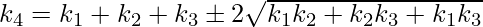
On solving the above equation we get the radius of the fourth circle. The formula for finding the fourth circle’s radius is:
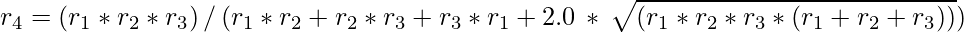
Thus if r1, r2, and r3 are known, r4 can easily be calculated using the above formula.
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
double findRadius(double r1, double r2, double r3)
{
double r4 = (r1 * r2 * r3)
/ (r1 * r2 + r2 * r3
+ r1 * r3 + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
return r4;
}
int main()
{
double r1 = 1;
double r2 = 1;
double r3 = 1;
double r4 = findRadius(r1, r2, r3);
cout << "The radius of fourth circle: " << r4;
return 0;
}
|
Java
import java.io.*;
class GFG
{
static double findRadius(double r1, double r2, double r3)
{
double r4 = (r1 * r2 * r3)
/ (r1 * r2 + r2 * r3
+ r1 * r3 + 2.0 * Math.sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
return r4;
}
public static void main (String[] args)
{
double r1 = 1;
double r2 = 1;
double r3 = 1;
double r4 = findRadius(r1, r2, r3);
System.out.println("The radius of fourth circle: " + r4);
}
}
|
Python3
from math import sqrt
def findRadius(r1, r2, r3):
r4 = (r1 * r2 * r3) / (r1 * r2 + r2 * r3 + r1 * r3 + 2.0 * sqrt(r1 * r2 * r3 * (r1 + r2 + r3)))
return r4
if __name__ == '__main__':
r1 = 1
r2 = 1
r3 = 1
r4 = findRadius(r1, r2, r3)
print("The radius of fourth circle:",r4)
|
C#
using System;
class GFG
{
static double findRadius(double r1, double r2, double r3)
{
double r4 = (r1 * r2 * r3)
/ (r1 * r2 + r2 * r3
+ r1 * r3 + 2.0 * Math.Sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
return r4;
}
public static void Main (String[] args)
{
double r1 = 1;
double r2 = 1;
double r3 = 1;
double r4 = Math.Round(findRadius(r1, r2, r3),6);
Console.Write("The radius of fourth circle: " + r4);
}
}
|
Javascript
<script>
function findRadius(r1, r2, r3) {
let r4 =
(r1 * r2 * r3) /
(r1 * r2 +
r2 * r3 +
r1 * r3 +
2.0 * Math.sqrt(r1 * r2 * r3 * (r1 + r2 + r3)));
return r4.toFixed(6);
}
let r1 = 1;
let r2 = 1;
let r3 = 1;
let r4 = findRadius(r1, r2, r3);
document.write("The radius of fourth circle: " + r4);
</script>
|
OutputThe radius of fourth circle: 0.154701
Time complexity: O(log(r1 * r2 * r3 * (r1 + r2 + r3)))
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...