Count the nodes in the given tree whose weight is prime
Last Updated :
19 Sep, 2023
Given a tree, and the weights of all the nodes, the task is to count the number of nodes whose weight is prime.
Examples:
Input:
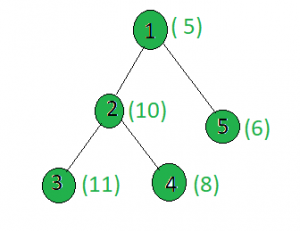
Output: 2
Only the weights of the nodes 1 and 3 are prime.
Algorithm:
Step 1: Start
Step 2: Initialize static variable of int type with 0 which will count a number of nodes with prime weight.
Step 3: Create a Static vector to store integer value and name it “graph”.
Step 4: Create a static array of integer type to store the weights of the node
Step 5: Create a function of the static type and name it “isprime” which takes an integer value as a parameter.
a. will return true if the number or weight is prime and false if it is not prime.
Step 6: Create a static function named it “dfs” with a void return type that takes node and parent as input.
a. If the weight of the current node is a prime, the dfs() method will add one to the global variable and.
b. To prevent returning to the previous node, iterate through the current node’s nearby nodes, calling the dfs() method recursively for each one except for the parent node.
Step 7: End
Approach: Perform dfs on the tree and for every node, check if it’s weight is prime or not.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int ans = 0;
vector<int> graph[100];
vector<int> weight(100);
bool isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
void dfs(int node, int parent)
{
if (isprime(weight[node]))
ans += 1;
for (int to : graph[node]) {
if (to == parent)
continue;
dfs(to, node);
}
}
int main()
{
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push_back(2);
graph[2].push_back(3);
graph[2].push_back(4);
graph[1].push_back(5);
dfs(1, 1);
cout << ans;
return 0;
}
|
Java
import java.util.*;
class GFG{
static int ans = 0;
static Vector<Integer>[] graph = new Vector[100];
static int[] weight = new int[100];
static boolean isprime(int n)
{
for (int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
static void dfs(int node, int parent)
{
if (isprime(weight[node]))
ans += 1;
for (int to : graph[node]) {
if (to == parent)
continue;
dfs(to, node);
}
}
public static void main(String[] args)
{
for (int i = 0; i < 100; i++)
graph[i] = new Vector<>();
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].add(2);
graph[2].add(3);
graph[2].add(4);
graph[1].add(5);
dfs(1, 1);
System.out.print(ans);
}
}
|
Python3
ans = 0
graph = [[] for i in range(100)]
weight = [0] * 100
def isprime(n):
i = 2
while(i * i <= n):
if (n % i == 0):
return False
i += 1
return True
def dfs(node, parent):
global ans
if (isprime(weight[node])):
ans += 1;
for to in graph[node]:
if (to == parent):
continue
dfs(to, node)
weight[1] = 5
weight[2] = 10
weight[3] = 11
weight[4] = 8
weight[5] = 6
graph[1].append(2)
graph[2].append(3)
graph[2].append(4)
graph[1].append(5)
dfs(1, 1)
print(ans)
|
C#
using System;
using System.Collections;
using System.Collections.Generic;
using System.Text;
class GFG{
static int ans = 0;
static ArrayList[] graph = new ArrayList[100];
static int[] weight = new int[100];
static bool isprime(int n)
{
for(int i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
static void dfs(int node, int parent)
{
if (isprime(weight[node]))
ans += 1;
foreach(int to in graph[node])
{
if (to == parent)
continue;
dfs(to, node);
}
}
public static void Main(string[] args)
{
for(int i = 0; i < 100; i++)
graph[i] = new ArrayList();
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].Add(2);
graph[2].Add(3);
graph[2].Add(4);
graph[1].Add(5);
dfs(1, 1);
Console.Write(ans);
}
}
|
Javascript
<script>
let ans=0;
let graph = new Array(100);
let weight = new Array(100);
for(let i=0;i<100;i++)
{
graph[i]=[];
weight[i]=0;
}
function isprime(n)
{
for (let i = 2; i * i <= n; i++)
if (n % i == 0)
return false;
return true;
}
function dfs(node,parent)
{
if (isprime(weight[node]))
ans += 1;
for(let to=0;to<graph[node].length;to++)
{
if(graph[node][to] == parent)
continue
dfs(graph[node][to], node);
}
}
x = 15;
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push(2);
graph[2].push(3);
graph[2].push(4);
graph[1].push(5);
dfs(1, 1);
document.write( ans);
</script>
|
Complexity Analysis:
- Time Complexity: O(N*sqrt(V)), where V is the maximum weight of a node in the given tree.
In DFS, every node of the tree is processed once and hence the complexity due to the DFS is O(N) when there are N total nodes in the tree. Also, while processing every node, in order to check if the node value is prime or not, a loop up to sqrt(V) is being run, where V is the weight of the node. Hence for every node, there is an added complexity of O(sqrt(V)). Therefore, the time complexity is O(N*sqrt(V)).
- Auxiliary Space: O(1).
Any extra space is not required, so the space complexity is constant.
Another approach:
Approach Steps:
1. Define a struct for the binary tree node with an integer value, and left and right child pointers.
2. Write a function to check if a number is prime or not.
3. Write a recursive function to count the nodes in the tree whose weight is prime.
4. The base case for the recursive function is when the root node is NULL, in which case we return 0.
5. If the root node’s value is prime, we increment the count by 1.
6. Recursively call the function on the left and right subtrees and add the returned counts to the current count.
7. Return the final count.
C++
#include <cmath>
#include <iostream>
using namespace std;
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
bool is_prime(int num)
{
if (num <= 1) {
return false;
}
for (int i = 2; i <= num / 2; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
int count_prime_nodes(TreeNode* root)
{
if (root == NULL) {
return 0;
}
int count = 0;
if (is_prime(root->val)) {
count++;
}
count += count_prime_nodes(root->left);
count += count_prime_nodes(root->right);
return count;
}
int main()
{
TreeNode* root = new TreeNode();
root->val = 5;
root->left = new TreeNode();
root->left->val = 3;
root->left->left = NULL;
root->left->right = NULL;
root->right = new TreeNode();
root->right->val = 7;
root->right->left = new TreeNode();
root->right->left->val = 2;
root->right->left->left = NULL;
root->right->left->right = NULL;
root->right->right = NULL;
int count = count_prime_nodes(root);
cout << "The number of nodes in the tree whose weight "
"is prime is "
<< count << endl;
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
bool is_prime(int num) {
if (num <= 1) {
return false;
}
for (int i = 2; i <= num/2; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
int count_prime_nodes(struct TreeNode* root) {
if (root == NULL) {
return 0;
}
int count = 0;
if (is_prime(root->val)) {
count++;
}
count += count_prime_nodes(root->left);
count += count_prime_nodes(root->right);
return count;
}
int main() {
struct TreeNode* root = (struct TreeNode*) malloc(sizeof(struct TreeNode));
root->val = 5;
root->left = (struct TreeNode*) malloc(sizeof(struct TreeNode));
root->left->val = 3;
root->left->left = NULL;
root->left->right = NULL;
root->right = (struct TreeNode*) malloc(sizeof(struct TreeNode));
root->right->val = 7;
root->right->left = (struct TreeNode*) malloc(sizeof(struct TreeNode));
root->right->left->val = 2;
root->right->left->left = NULL;
root->right->left->right = NULL;
root->right->right = NULL;
int count = count_prime_nodes(root);
printf("The number of nodes in the tree whose weight is prime is %d\n", count);
return 0;
}
|
Java
import java.lang.Math;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val)
{
this.val = val;
left = null;
right = null;
}
}
public class CountPrimeNodes {
static boolean isPrime(int num)
{
if (num <= 1) {
return false;
}
for (int i = 2; i <= Math.sqrt(num); i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
static int countPrimeNodes(TreeNode root)
{
if (root == null) {
return 0;
}
int count = 0;
if (isPrime(root.val)) {
count++;
}
count += countPrimeNodes(root.left);
count += countPrimeNodes(root.right);
return count;
}
public static void main(String[] args)
{
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.left.left = null;
root.left.right = null;
root.right = new TreeNode(7);
root.right.left = new TreeNode(2);
root.right.left.left = null;
root.right.left.right = null;
root.right.right = null;
int count = countPrimeNodes(root);
System.out.println(
"The number of nodes in the tree whose weight is prime is "
+ count);
}
}
|
Python3
import math
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def is_prime(num):
if num <= 1:
return False
for i in range(2, int(num/2)+1):
if num % i == 0:
return False
return True
def count_prime_nodes(root):
if root is None:
return 0
count = 0
if is_prime(root.val):
count += 1
count += count_prime_nodes(root.left)
count += count_prime_nodes(root.right)
return count
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(7)
root.right.left = TreeNode(2)
count = count_prime_nodes(root)
print(f"The number of nodes in the tree whose weight is prime is {count}")
|
C#
using System;
class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val = 0, TreeNode left = null, TreeNode right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
class MainClass {
static bool is_prime(int num) {
if (num <= 1) {
return false;
}
for (int i = 2; i <= num / 2; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
static int count_prime_nodes(TreeNode root) {
if (root == null) {
return 0;
}
int count = 0;
if (is_prime(root.val)) {
count++;
}
count += count_prime_nodes(root.left);
count += count_prime_nodes(root.right);
return count;
}
public static void Main() {
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.left.left = null;
root.left.right = null;
root.right = new TreeNode(7);
root.right.left = new TreeNode(2);
root.right.left.left = null;
root.right.left.right = null;
root.right.right = null;
int count = count_prime_nodes(root);
Console.WriteLine("The number of nodes in the tree whose weight is prime is " + count);
}
}
|
Javascript
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
function is_prime(num) {
if (num <= 1) {
return false;
}
for (let i = 2; i <= Math.floor(Math.sqrt(num)); i++) {
if (num % i === 0) {
return false;
}
}
return true;
}
function count_prime_nodes(root) {
if (root === null) {
return 0;
}
let count = 0;
if (is_prime(root.val)) {
count++;
}
count += count_prime_nodes(root.left);
count += count_prime_nodes(root.right);
return count;
}
let root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(7);
root.right.left = new TreeNode(2);
let count = count_prime_nodes(root);
console.log("The number of nodes in the tree whose weight is prime is " + count);
|
Output
The number of nodes in the tree whose weight is prime is 4
Time Complexity:
The time complexity of this algorithm is O(n), where n is the number of nodes in the binary tree, as we need to visit each node once.
Space Complexity:
The space complexity of this algorithm is O(h), where h is the height of the binary tree, as we need to store the call stack for the recursive function calls up to the maximum depth of the tree. In the worst case, the binary tree can be skewed, and the height of the tree can be equal to the number of nodes in the tree, in which case the space complexity is O(n).
Approach(Using BFS):This approach is similar to the DFS approach, except that we use a breadth-first search instead of a depth-first search.
Algorithm:
- Define a variable count and initialize it to 0.
- Define a function is_prime(n) that returns True if n is prime, and False otherwise.
- Define a function bfs(root) that performs a breadth-first search on the tree, starting from root.
- In bfs(root):
a. Define a queue q and add root to it.
b. While q is not empty:
i. Pop a node from q.
ii. If the weight of the node is prime, increment count.
iii. If the left child of the node exists, add it to q.
iv. If the right child of the node exists, add it to q.
- Call bfs(root), where root is the root node of the tree.
- Return count.
C++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
struct Node {
int weight;
vector<Node*> children;
};
bool isPrime(int n) {
if (n <= 1)
return false;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}
int countPrimeNodes(Node* root) {
int count = 0;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* current = q.front();
q.pop();
if (isPrime(current->weight))
count++;
for (Node* child : current->children)
q.push(child);
}
return count;
}
int main() {
Node* root = new Node{ 5, {} };
Node* node1 = new Node{ 4, {} };
Node* node2 = new Node{ 3, {} };
Node* node3 = new Node{ 7, {} };
Node* node4 = new Node{ 2, {} };
root->children.push_back(node1);
root->children.push_back(node2);
node1->children.push_back(node3);
node2->children.push_back(node4);
int primeCount = countPrimeNodes(root);
cout << "Number of nodes whose weight is prime: " << primeCount << endl;
delete node4;
delete node3;
delete node2;
delete node1;
delete root;
return 0;
}
|
Java
import java.util.*;
class Node {
int weight;
List<Node> children;
Node(int weight) {
this.weight = weight;
this.children = new ArrayList<>();
}
}
public class Main {
static boolean isPrime(int n) {
if (n <= 1)
return false;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}
static int countPrimeNodes(Node root) {
int count = 0;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node current = queue.poll();
if (isPrime(current.weight))
count++;
for (Node child : current.children)
queue.add(child);
}
return count;
}
public static void main(String[] args) {
Node root = new Node(5);
Node node1 = new Node(4);
Node node2 = new Node(3);
Node node3 = new Node(7);
Node node4 = new Node(2);
root.children.add(node1);
root.children.add(node2);
node1.children.add(node3);
node2.children.add(node4);
int primeCount = countPrimeNodes(root);
System.out.println("Number of nodes whose weight is prime: " + primeCount);
}
}
|
Python3
from queue import Queue
class Node:
def __init__(self, weight):
self.weight = weight
self.children = []
def is_prime(n):
if n <= 1:
return False
for i in range(2, int(n ** 0.5) + 1):
if n % i == 0:
return False
return True
def count_prime_nodes(root):
count = 0
q = Queue()
q.put(root)
while not q.empty():
current = q.get()
if is_prime(current.weight):
count += 1
for child in current.children:
q.put(child)
return count
if __name__ == '__main__':
root = Node(5)
node1 = Node(4)
node2 = Node(3)
node3 = Node(7)
node4 = Node(2)
root.children.extend([node1, node2])
node1.children.append(node3)
node2.children.append(node4)
prime_count = count_prime_nodes(root)
print("Number of nodes whose weight is prime:", prime_count)
|
C#
using System;
using System.Collections.Generic;
namespace PrimeNodeCount
{
public class Node
{
public int Weight;
public List<Node> Children = new List<Node>();
}
class Program
{
static bool IsPrime(int n)
{
if (n <= 1)
return false;
for (int i = 2; i * i <= n; i++)
{
if (n % i == 0)
return false;
}
return true;
}
static int CountPrimeNodes(Node root)
{
int count = 0;
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
while (q.Count > 0)
{
Node current = q.Dequeue();
if (IsPrime(current.Weight))
count++;
foreach (Node child in current.Children)
q.Enqueue(child);
}
return count;
}
static void Main(string[] args)
{
Node root = new Node { Weight = 5 };
Node node1 = new Node { Weight = 4 };
Node node2 = new Node { Weight = 3 };
Node node3 = new Node { Weight = 7 };
Node node4 = new Node { Weight = 2 };
root.Children.Add(node1);
root.Children.Add(node2);
node1.Children.Add(node3);
node2.Children.Add(node4);
int primeCount = CountPrimeNodes(root);
Console.WriteLine("Number of nodes whose weight is prime: " + primeCount);
}
}
}
|
Javascript
class Node {
constructor(weight, children) {
this.weight = weight;
this.children = children || [];
}
}
function isPrime( n) {
if (n <= 1)
return false;
for (let i = 2; i * i <= n; i++) {
if (n % i == 0)
return false;
}
return true;
}
function countPrimeNodes(root) {
let count = 0;
let q = [root];
while (q.length > 0) {
let current = q.shift();
if (isPrime(current.weight))
count++;
for (let child of current.children)
q.push(child);
}
return count;
}
let root = new Node(5, []);
let node1 = new Node(4, []);
let node2 = new Node(3, []);
let node3 = new Node(7, []);
let node4 = new Node(2, []);
root.children.push(node1, node2);
node1.children.push(node3);
node2.children.push(node4);
let primeCount = countPrimeNodes(root);
console.log("Number of nodes whose weight is prime: " + primeCount);
|
Output
Number of nodes whose weight is prime: 4
Time Complexity: O(N), where N is the number of nodes in the tree. This is because the code performs a BFS traversal of the tree, visiting each node once, and checking if its weight is prime. The isPrime function has a time complexity of O(sqrt(N)), which is the worst-case scenario when the input number is prime. However, since the isPrime function is called only on the weights of the nodes, the overall time complexity of the code is O(N).
Auxiliary Space: O(N), where N is the number of nodes in the tree. This is because the code uses a queue to perform the BFS traversal, and the size of the queue can be at most N in the worst case when the tree is a complete binary tree. Additionally, the Node structure has a children vector that stores the child nodes of each node. The size of the children vector can be at most N-1 in the worst case, where each node has only one child except for the root node. Therefore, the total auxiliary space used by the code is O(N + N-1), which simplifies to O(N).
Share your thoughts in the comments
Please Login to comment...