Count the nodes in the given tree whose weight is even parity
Last Updated :
28 Feb, 2023
Given a tree and the weights of all the nodes, the task is to count the number of nodes whose weights are even parity i.e. whether the count of set bits in them is even.
Examples:
Input:
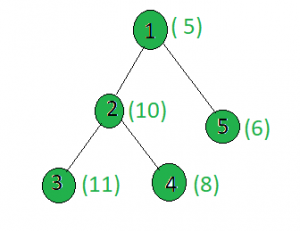
Output: 3
| Weight |
Binary Representation |
Parity |
| 5 |
0101 |
Even |
| 10 |
1010 |
Even |
| 11 |
1011 |
Odd |
| 8 |
1000 |
Odd |
| 6 |
0110 |
Even |
Approach: Perform dfs on the tree and for every node, check if its weight is even parity or not. If yes then increment count.
Steps to solve the problem:
- Initialize ans to 0.
- Define a function isEvenParity(x) that takes an integer x and returns true if the count of set bits in x is even and false otherwise.
- Define a function dfs(node, parent) that performs depth-first search on the graph.
- Within the dfs function:
a. Check if the weight of the current node has even parity using the isEvenParity function. If it does, increment ans by 1.
b. For each neighbor to of node in the graph, if it is not equal to the parent, recursively call dfs with to as the node and node as the parent.
- Return ans as the final result.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int ans = 0;
vector<int> graph[100];
vector<int> weight(100);
bool isEvenParity(int x)
{
int parity = 0;
while (x != 0) {
x = x & (x - 1);
parity++;
}
if (parity % 2 == 0)
return true;
else
return false;
}
void dfs(int node, int parent)
{
if (isEvenParity(weight[node]))
ans += 1;
for (int to : graph[node]) {
if (to == parent)
continue;
dfs(to, node);
}
}
int main()
{
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push_back(2);
graph[2].push_back(3);
graph[2].push_back(4);
graph[1].push_back(5);
dfs(1, 1);
cout << ans;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int ans = 0;
static Vector<Vector<Integer>> graph = new Vector<Vector<Integer>>();
static Vector<Integer> weight = new Vector<Integer>();
static boolean isEvenParity(int x)
{
int parity = 0;
while (x != 0)
{
x = x & (x - 1);
parity++;
}
if (parity % 2 == 0)
return true;
else
return false;
}
static void dfs(int node, int parent)
{
if (isEvenParity(weight.get(node) ))
ans += 1;
for (int i = 0; i < graph.get(node).size(); i++)
{
if (graph.get(node).get(i) == parent)
continue;
dfs(graph.get(node).get(i) , node);
}
}
public static void main(String args[])
{
weight.add( 0);
weight.add( 5);
weight.add( 10);;
weight.add( 11);;
weight.add( 8);
weight.add( 6);
for(int i=0;i<100;i++)
graph.add(new Vector<Integer>());
graph.get(1).add(2);
graph.get(2).add(3);
graph.get(2).add(4);
graph.get(1).add(5);
dfs(1, 1);
System.out.println( ans );
}
}
|
Python3
ans = 0
graph = [[] for i in range(100)]
weight = [0]*100
def isEvenParity(x):
parity = 0
while (x != 0):
x = x & (x - 1)
parity += 1
if (parity % 2 == 0):
return True
else:
return False
def dfs(node, parent):
global ans
if (isEvenParity(weight[node])):
ans += 1
for to in graph[node]:
if (to == parent):
continue
dfs(to, node)
weight[1] = 5
weight[2] = 10
weight[3] = 11
weight[4] = 8
weight[5] = 6
graph[1].append(2)
graph[2].append(3)
graph[2].append(4)
graph[1].append(5)
dfs(1, 1)
print(ans)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int ans = 0;
static List<List<int>> graph = new List<List<int>>();
static List<int> weight = new List<int>();
static bool isEvenParity(int x)
{
int parity = 0;
while (x != 0)
{
x = x & (x - 1);
parity++;
}
if (parity % 2 == 0)
return true;
else
return false;
}
static void dfs(int node, int parent)
{
if (isEvenParity(weight[node]))
ans += 1;
for (int i = 0; i < graph[node].Count; i++)
{
if (graph[node][i] == parent)
continue;
dfs(graph[node][i] , node);
}
}
static void Main()
{
weight.Add(0);
weight.Add(5);
weight.Add(10);
weight.Add(11);
weight.Add(8);
weight.Add(6);
for(int i = 0; i < 100; i++)
graph.Add(new List<int>());
graph[1].Add(2);
graph[2].Add(3);
graph[2].Add(4);
graph[1].Add(5);
dfs(1, 1);
Console.WriteLine( ans );
}
}
|
Javascript
<script>
let ans = 0;
let graph = new Array(100);
let weight = new Array(100);
for(let i = 0; i < 100; i++)
{
graph[i] = [];
weight[i] = 0;
}
function isEvenParity(x)
{
let parity = 0;
while (x != 0) {
x = x & (x - 1);
parity++;
}
if (parity % 2 == 0)
return true;
else
return false;
}
function dfs(node, parent)
{
if (isEvenParity(weight[node]))
ans += 1;
for(let to=0;to<graph[node].length;to++) {
if(graph[node][to] == parent)
continue
dfs(graph[node][to], node);
}
}
weight[1] = 5;
weight[2] = 10;
weight[3] = 11;
weight[4] = 8;
weight[5] = 6;
graph[1].push(2);
graph[2].push(3);
graph[2].push(4);
graph[1].push(5);
dfs(1, 1);
document.write(ans);
</script>
|
Complexity Analysis:
- Time Complexity: O(N).
In DFS, every node of the tree is processed once and hence the complexity due to the DFS is O(N) for N nodes in the tree. Therefore, the time complexity is O(N).
- Auxiliary Space: O(1).
Any extra space is not required, so the space complexity is constant.
Share your thoughts in the comments
Please Login to comment...