Count the nodes in the given tree whose weight is even

Given a tree, and the weights of all the nodes, the task is to count the number of nodes whose weight is even.
Examples:

Input:

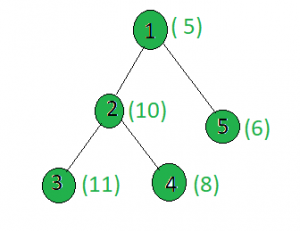
Output: 3 
Only the weights of the nodes 2, 4 and 5 are even. 

Approach: Perform dfs on the tree and for every node, check if it’s weight is divisible by 2 or not. If yes then increment count.

Algorithm:

Step 1: Start
Step 2: Create a global integer variable name it as “ans” and initialize it to 0.
Step 3: Create a vector of integer type name it as “weight” to store the weights of the nodes.
Step 4: Create a vector of integer type name it as “graph” to represent the tree.
Step 5: Create a static function of void return type name it as “dfs” which take node and its parent as input.
Step 6: The value of ans should be increased by one if the weight of the current node is even.
Step 7: Start a for loop for all graph node 
a. if current node equal to parent then Recursively call the dfs function with the current node and the next node as n                    parameters.
Step 8: End

Below is the implementation of the above approach:

C++

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;

int ans = 0;

vector<int> graph[100];
vector<int> weight(100);

// Function to perform dfs
void dfs(int node, int parent)
{
    // If weight of the current node is even
    if (weight[node] % 2 == 0)
        ans += 1;

    for (int to : graph[node]) {
        if (to == parent)
            continue;
        dfs(to, node);
    }
}

// Driver code
int main()
{
    int x = 15;

    // Weights of the node
    weight[1] = 5;
    weight[2] = 10;
    weight[3] = 11;
    weight[4] = 8;
    weight[5] = 6;

    // Edges of the tree
    graph[1].push_back(2);
    graph[2].push_back(3);
    graph[2].push_back(4);
    graph[1].push_back(5);

    dfs(1, 1);

    cout << ans;

    return 0;
}

Java

// Java implementation of the approach
import java.util.*;

class GFG
{
    static int ans = 0;

    @SuppressWarnings("unchecked")
    static Vector<Integer>[] graph = new Vector[100];
    static int[] weight = new int[100];

    // Function to perform dfs
    static void dfs(int node, int parent)
    {
        // If weight of the current node is even
        if (weight[node] % 2 == 0)
            ans += 1;

        for (int to : graph[node])
        {
            if (to == parent)
                continue;
            dfs(to, node);
        }
    }

    // Driver code
    public static void main(String[] args)
    {
        int x = 15;

    for (int i = 0; i < 100; i++)
            graph[i] = new Vector<>();

        // Weights of the node
        weight[1] = 5;
        weight[2] = 10;
        weight[3] = 11;
        weight[4] = 8;
        weight[5] = 6;

        // Edges of the tree
        graph[1].add(2);
        graph[2].add(3);
        graph[2].add(4);
        graph[1].add(5);

        dfs(1, 1);

        System.out.println(ans);
    }
}

// This code is contributed by shubhamsingh10

Python3

# Python3 implementation of the approach
ans = 0

graph = [[] for i in range(100)]
weight = [0] * 100

# Function to perform dfs
def dfs(node, parent):
    global ans

    # If weight of the current node is even
    if (weight[node] % 2 == 0):
        ans += 1

    for to in graph[node]:
        if (to == parent):
            continue
        dfs(to, node)

# Driver code
x = 15

# Weights of the node
weight[1] = 5
weight[2] = 10
weight[3] = 11
weight[4] = 8
weight[5] = 6

# Edges of the tree
graph[1].append(2)
graph[2].append(3)
graph[2].append(4)
graph[1].append(5)

dfs(1, 1)
print(ans)

# This code is contributed by SHUBHAMSINGH10

C#

// C# implementation of the approach
using System;
using System.Collections.Generic;

class GFG
{
    static int ans = 0;
    static List<int>[] graph = new List<int>[100];
    static int[] weight = new int[100];

    // Function to perform dfs
    static void dfs(int node, int parent)
    {
        // If weight of the current node is even
        if (weight[node] % 2 == 0)
            ans += 1;

        foreach (int to in graph[node])
        {
            if (to == parent)
                continue;
            dfs(to, node);
        }
    }

    // Driver code
    public static void Main(String[] args)
    {
        for (int i = 0; i < 100; i++)
            graph[i] = new List<int>();

        // Weights of the node
        weight[1] = 5;
        weight[2] = 10;
        weight[3] = 11;
        weight[4] = 8;
        weight[5] = 6;

        // Edges of the tree
        graph[1].Add(2);
        graph[2].Add(3);
        graph[2].Add(4);
        graph[1].Add(5);

        dfs(1, 1);

        Console.WriteLine(ans);
    }
}

// This code is contributed by Rajput-Ji

Javascript

<script>
// Javascript implementation of the approach
    let ans = 0;
    let graph = new Array(100);
    let weight = new Array(100);
    for(let i = 0; i < 100; i++)
    {
        graph[i] = [];
        weight[i] = 0;
    }

    // Function to perform dfs
    function dfs(node, parent)
    {

        // If weight of the current node is even
        if (weight[node] % 2 == 0)
        {
            ans += 1;
        }

        for (let to=0;to<graph[node].length ;to++)
        {

            if (graph[node][to] == parent)
               {
                continue;
            }
            dfs(graph[node][to], node);
        }
    }

    // Driver code
    let x = 15;

    // Weights of the node
        weight[1] = 5;
        weight[2] = 10;
        weight[3] = 11;
        weight[4] = 8;
        weight[5] = 6;

        // Edges of the tree
        graph[1].push(2);
        graph[2].push(3);
        graph[2].push(4);
        graph[1].push(5);
        dfs(1, 1);
        document.write(ans);

    // This code is contributed by unknown2108
</script>

Output:

3

Complexity Analysis:

• Time Complexity : O(N). 
  In dfs, every node of the tree is processed once and hence the complexity due to the dfs is O(N) if there are total N nodes in the tree. Therefore, the time complexity is O(N).
• Auxiliary Space : O(1). 
  Any extra space is not required, so the space complexity is constant.