Coordinate Geometry Class 10 Maths Notes Chapter 7

Last Updated : 19 Jun, 2023

CBSE Class 10 Maths Notes Chapter 7 Coordinate Geometry are provided to support student’s education. We believe that students’ learning and development are of the utmost importance, and that’s why we have created these comprehensive notes to help them comprehend the complex subject of Coordinate Geometry better.

The NCERT Class 10 Maths textbook’s Chapter 7 explores the realm of Coordinate Geometry and covers various concepts such as distance formula, section formula, and more. Our notes aim to provide students with a complete summary of the entire chapter, including all essential topics, formulae, and concepts necessary to succeed in their exams.

What is Coordinate Geometry?

In the field of mathematics known as coordinate geometry, geometric figures are studied using coordinates. It also goes by the name of analytical geometry.

Determine the distance between two points
Determine the point which divides the line in ratio m:n
Locate the midpoint of a line segment
Determine the area of a triangle using three coordinate points

Coordinate geometry is a powerful tool that can be used to solve a wide variety of geometric problems. Let’s learn about it in this article.

x-Coordinate or Abscissa

The horizontal separation between a point and the origin, which is the point where the x- and y-axes connect, is known as the x-coordinate. It is also called the abscissa.

y-Coordinate or Ordinate

The y-coordinate, on the other hand, represents the vertical distance of a point from the origin. It is also called the ordinate.

Cartesian Plane

In the Cartesian plane (also known as the xy-plane or rectangular coordinate system), all points are represented as ordered pairs (x, y), where x represents the x-coordinate and y represents the y-coordinate.
Points to the right of the y-axis have positive x-coordinates, indicating they are situated in the positive x-direction. Points left of the y-axis, on the other hand, have negative x-coordinates, indicating that they are situated in the negative x-direction.
For y-coordinates, points located above the x-axis have positive values, indicating they are in the positive y-direction.
Points lying on the x-axis have a y-coordinate of zero since their vertical distance from the origin is zero. Similarly, points lying on the y-axis have an x-coordinate of zero since their horizontal distance from the origin is zero.
The origin, with coordinates (0, 0), serves as the reference point for the Cartesian plane. Points below the x-axis have negative y-coordinates, indicating that they are in the y-direction.

Distance Formula

As distance can never be negative, thus we only take the positive square root of the number to find the distance between any two points using the distance formula.

The distance between the points P(x₁, y₁) and Q(x₂, y₂) is

$\bold{PQ=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}$

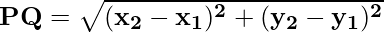
The distance of a point P(x, y) from the origin O(0, 0) is given by

$\bold{OP=\sqrt{x^2+y^2}}$

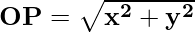
Note:

To prove that a square is a square, one needs to show that all four sides are equal in length and that the diagonals are also equal in length.
To prove that a rhombus is a rhombus, one needs to show that all four sides are equal in length.
To prove that a rectangle is a rectangle, one needs to show that opposite sides are equal in length and that the diagonals are also equal in length.
To prove that a parallelogram is a parallelogram, one needs to show that opposite sides are equal in length.
To prove that a figure is a parallelogram but not a rectangle, one needs to show that opposite sides are equal in length but the diagonals are not equal in length.
To prove that a rhombus is a rhombus but not a square, one needs to show that all sides are equal in length but the diagonals are not equal in length.
To prove that three points are collinear, one needs to show that the sum of the distance between two pairs of points is equal to the distance between the third pair of points.

Example: Find the distance between the points P(−6, 7) and Q (−1, −5).

Solution:

Here, x₁ = −6, x₂ = −1, y₁ = 7 and y₂ = −5

Substitute the above values in the distance formula.

$PQ=\sqrt{(-1-(-6))^2+(-5-7)^2}$

$\Rightarrow{PQ=\sqrt{(5)^2+(-12)^2}}$

$\Rightarrow{PQ=\sqrt{25+144}}$

$\Rightarrow{PQ=\sqrt{169}}$

\ $\Rightarrow{PQ=13}$

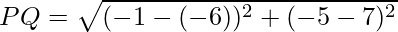
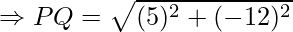
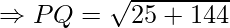
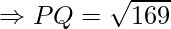
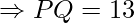
Therefore, the distance between the points P(−6, 7) and Q (−1, −5) is 13.

Example: Prove that the points A(1, 7), B(4, 2), C(−1, −1) and D(−4, 4) are the vertices of a square.

Solution:

First, calculate the length of all sides.

$AB=\sqrt{(4-1)^2+(2-7)^2}$

$\Rightarrow{AB=\sqrt{3^2+(-5)^2}}$

$\Rightarrow{AB=\sqrt{9+25}}$

$\Rightarrow{AB=\sqrt{34}}$

$BC=\sqrt{(-1-4)^2+(-1-2)^2}$

$\Rightarrow{BC=\sqrt{(-5)^2+(-3)^2}}$

$\Rightarrow{BC=\sqrt{25+9}}$

$\Rightarrow{BC=\sqrt{34}}$

$CD=\sqrt{(-4-(-1))^2+(4-(-1))^2}$

$\Rightarrow{CD=\sqrt{(-3)^2+(5)^2}}$

$\Rightarrow{CD=\sqrt{9+25}}$

$\Rightarrow{CD=\sqrt{34}}$

$DA=\sqrt{(1-(-4))^2+(7-4)^2}$

$\Rightarrow{DA=\sqrt{(5)^2+(3)^2}}$

$\Rightarrow{DA=\sqrt{25+9}}$

$\Rightarrow{DA=\sqrt{34}}$

$AC=\sqrt{(-1-1)^2+(-1-7)^2}$

$\Rightarrow{AC=\sqrt{(-2)^2+(-8)^2}}$

$\Rightarrow{AC=\sqrt{4+64}}$

$\Rightarrow{AC=\sqrt{68}}$

$\Rightarrow{AC=2\sqrt{17}}$

$BD=\sqrt{(-4-4)^2+(4-2)^2}$

$\Rightarrow{BD=\sqrt{(-8)^2+(2)^2}}$

$\Rightarrow{BD=\sqrt{64+4}}$

$\Rightarrow{BD=\sqrt{68}}$

$\Rightarrow{BD=2\sqrt{17}}$

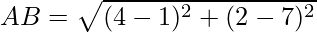
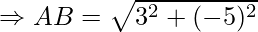
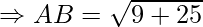
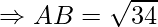
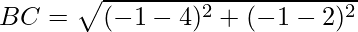
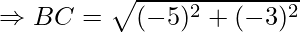
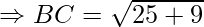
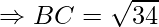
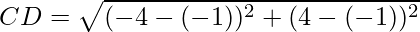
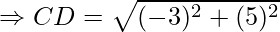
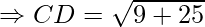
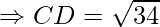
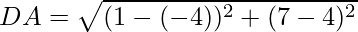
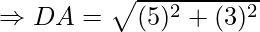
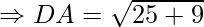
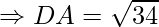
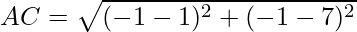
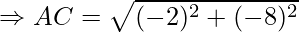
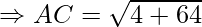
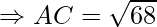
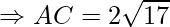
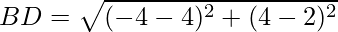
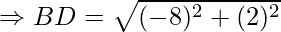
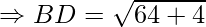
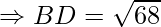
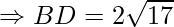
AC = BD = 2√17

AB = BC = CD = DA = √34

All sides are equal.

Diagonals are equal.

Hence, it is proved that the points A(1, 7), B(4, 2), C(−1, −1) and D(−4, 4) are the vertices of a square.

Section Formula

The section formula is a formula in coordinate geometry that is used to find the coordinates of a point that divides a line segment in a given ratio. The formula is as follows:

$\bold{(x=\frac{mx_2+nx_1}{m+n},y=\frac{my_2+my_1}{m+n})}$

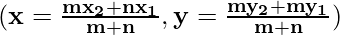
If P is the midpoint of AB, then it divides AB in ratio k : 1, so its coordinates are

$\bold{(\frac{k\cdot{x}_1+1\cdot{x}_2}{k+1},\frac{k\cdot{y}_1+1\cdot{y}_2}{k+1})=(\frac{k{x}_1+{x}_2}{k+1},\frac{k{y}_1+{y}_2}{k+1})}$ .

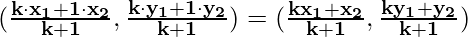Mid-Point Formula

If P is the midpoint of AB, then it divides AB in a ratio of 1:1, so its coordinates are

$\bold{(\frac{1\cdot{x}_1+1\cdot{x}_2}{1+1},\frac{1\cdot{y}_1+1\cdot{y}_2}{1+1})=(\frac{{x}_1+{x}_2}{2},\frac{{y}_1+{y}_2}{2})}$

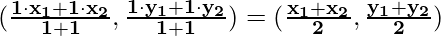
Note: This formula is also called as mid-point formula.

Example 1: Find the coordinates of the point which divides the line segment joining the points (6, 3) and (-4, 5) in the ratio 3 : 2 internally.

Solution:

Let us assume a point P (x, y) which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 : 2 internally.

Here, m = 3, n = 2, x₁ = 6, y₁ = 3, x₂ = −4 and y₂ = 5.

Substitute all the above values in section formula.

$(\frac{3(-4)+2(6)}{3+2},\frac{5(5)+2(3)}{3+2})=(0, \frac{21}{5})$

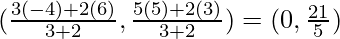
Therefore, the coordinates of P are (0, 21/5).

Example 2: In what ratio does point C (3/5, 11/5) divide the line segment joining points A (3, 5) and B (−3, −2)?

Solution:

Let us assume the point C divide AB in the ratio λ : 1.

Here, x₁ = 3, y₁ = 5, x₂ = −3 and y₂ = −2

$(\frac{k\cdot(-3)+1\cdot(3)}{k+1},\frac{k\cdot(-2)+1\cdot(5)}{k+1})=(\frac{-3k+3}{k+1},\frac{-2k+5}{k+1})$

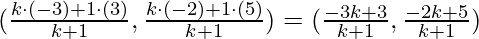
The coordinates of C is given by (3/5, 11/5)

$\frac{-3k+3}{k+1}=\frac{3}{5}$

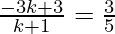
⇒ 3(k + 1) = 5(−3k+3)

⇒ 3k + 3 = −15k + 15

⇒ 18k = 12

⇒ k = 2/3

$\frac{-2k+5}{k+1}=\frac{11}{5}$

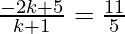
⇒ 11(k + 1) = 5 (−2k+5)

⇒ 11k + 11 = −10k + 25

⇒ 21k = 14

⇒ k = 2/3

Hence, the point C divides AB in the ratio 2 : 3.

Example 3: The three vertices of a parallelogram taken in order are (−1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.

Solution:

Let the fourth vertex be D (x, y).

Since, the diagonals of a parallelogram bisect each other.

Mid-point of AC = Mid-point of BD

$(\frac{-1+2}{2}, \frac{0+2}{2})=(\frac{3+x}{2}, \frac{1+y}{2})$

$(\frac{1}{2},1)=(\frac{3+x}{2},\frac{y+1}{2})$

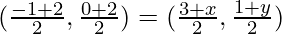
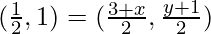
Compare the coordinates.

$\frac{3+x}{2}=\frac{1}{2}$

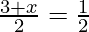
3 + x = 1 ⇒x = −2

(y + 1)/ 2=1

y + 1 = 2

y = 1

Hence, the fourth vertex of parallelogram is (−2, 1).

Area of Triangle

The area of a triangle, the coordinates of whose vertices are (x₁, y₁), (x₂, y₂), and (x₃, y₃) is

$\bold{\text{Area of triangle}=\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]}$

Example: Find the area of a triangle whose vertices are A(3, 2), B(11, 8), and C(8, 12).

Solution:

$\text{Area of triangle}=\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]$

$\Rightarrow{=\frac{1}{2}(3(8-12)+11(12-2)+8(2-8)}\\ \Rightarrow{=\frac{1}{2}(-12+110-48}\\ \Rightarrow{=25 \text{ sq. units}}$

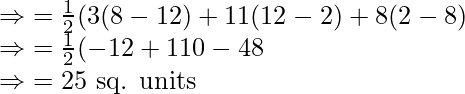
Also, Read

NCERT Solutions for Coordinate Geometry
CBSE Class 10 Maths Notes

FAQs on NCERT Notes for Class 10 Maths Chapter 7 Coordinate Geometry

Q1: What is Coordinate Geometry?

Answer:

Coordinate geometry, which is also referred to as analytic geometry, is a mathematical field that integrates algebraic methods with geometric principles. It revolves around the examination of geometric shapes through the utilization of a coordinate system, where points are expressed as ordered pairs of numbers known as coordinates.

Q2: What is a Cartesian Plane?

Answer:

The Cartesian plane, also known as the Coordinate plane, is a flat, two-dimensional surface created by two perpendicular lines known as axes. These axes are labeled as the x-axis, which is horizontal, and the y-axis, which is vertical. The point at which the two axes intersect is referred to as the origin and is represented by the coordinates (0, 0).

Q3: What are Coordinates?

Answer:

Coordinates consist of pairs of numbers that indicate the precise position of a point within a coordinate plane. In a two-dimensional Cartesian coordinate system, these coordinates are typically denoted as (x, y), where the value of x represents the horizontal position, also known as the abscissa, and the value of y represents the vertical position, also known as the ordinate.

Q4: What is the Distance Formula?

Answer:

The distance formula is used to find the distance between two points in a coordinate plane. For two points with coordinates (x₁, y₁) and (x₂, y₂), the distance formula is given by:

$\bold{D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} }$

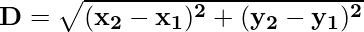
Q5: What is the Midpoint Formula?

Answer:

The midpoint formula is used to find the coordinates of the midpoint between two points in a coordinate plane. For two points with coordinates (x₁, y₁) and (x₂, y₂), the midpoint formula is:

$\bold{(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})}$

Suggest improvement

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

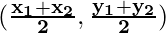
Share your thoughts in the comments

Coordinate Geometry Class 10 Maths Notes Chapter 7

What is Coordinate Geometry?

x-Coordinate or Abscissa

y-Coordinate or Ordinate

Cartesian Plane

Distance Formula

Section Formula

Mid-Point Formula

Area of Triangle

FAQs on NCERT Notes for Class 10 Maths Chapter 7 Coordinate Geometry

Q1: What is Coordinate Geometry?

Q2: What is a Cartesian Plane?

Q3: What are Coordinates?

Q4: What is the Distance Formula?

Q5: What is the Midpoint Formula?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?