Continuous Kernel Convolution
Last Updated :
14 Apr, 2023
Continuous Kernel convolution was proposed by the researcher of Verije University Amsterdam in collaboration with the University of Amsterdam in a paper titled ‘CKConv: Continuous Kernel Convolution For Sequential Data‘. The motivation behind that is to propose a model that uses the properties of convolution neural networks and Recurrent Neural networks in order to process a long sequence of image data.
Continuous Kernel Convolution (CKC) is a type of convolution operation used in deep learning for processing continuous input signals such as audio, speech, or sensor data. Unlike the standard discrete convolution operation used for processing digital signals, CKC uses a continuous kernel that can smoothly interpolate between different points in the input signal.
- In CKC, the continuous kernel is defined as a function of time, which can be represented using a Gaussian or a polynomial function. The kernel is then convolved with the input signal at each time step, producing an output signal that is also continuous.
- One of the advantages of CKC over standard discrete convolution is that it can capture fine-grained temporal information in the input signal, allowing the network to learn more precise patterns and features. CKC can also be used to interpolate and upsample signals, which is useful for tasks such as audio generation or speech synthesis.
- However, CKC can be computationally expensive and requires specialized hardware and software for efficient implementation. It also requires careful tuning of the kernel parameters to achieve good performance.
CKC has been used in various applications such as speech recognition, audio synthesis, and sensor data processing. It has also been extended to other types of continuous input signals such as video and 3D point clouds.
References:
- Binkowski, M., Donahue, J., & Simonyan, K. (2019). High-Resolution Image Synthesis and Semantic Manipulation with Conditional Continuous Convolutional
- Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 6728-6737).
- Kim, Y., & Lee, H. (2021). Continuous Kernel Convolutional Neural Networks for Audio Analysis. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 29, 459-471.
- Kondor, R., & Trivedi, S. (2018). On the generalization of equivariance and convolution in neural networks to the action of compact groups. In Advances in neural information processing systems (pp. 8533-8543).
Advantages:
- Continuous kernel convolution can capture fine-grained temporal information in the input signal, allowing the network to learn more precise patterns and features.
- It can be used to interpolate and upsample signals, which is useful for tasks such as audio generation or speech synthesis.
- It can handle continuous signals such as audio, speech, or sensor data more effectively than discrete convolution.
- CKC can also be used to model variable-length input sequences, making it suitable for tasks such as speech recognition or natural language processing.
Disadvantages:
- CKC is computationally expensive and requires specialized hardware and software for efficient implementation.
- It requires careful tuning of the kernel parameters to achieve good performance.
- CKC is not suitable for processing discrete or categorical input data such as images or text.
- It is a relatively new and less explored technique in deep learning, which means that there is less research and practical experience available for practitioners compared to traditional convolutional neural networks.
Convolution Operation
Let x ∶R → RNc and ψ ∶ R → RNc be a vector-valued signal and kernel on R, such that x = {xc}Nc and ψ = {ψc} NC c=1. The convolution operation can be defined as:
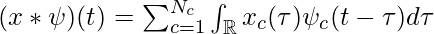
However, practically the input signal x is gather from sampling. Thus, the input signal and convolution can be defined as
- Input signal:
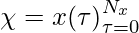
- Convolution:
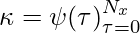
and the equation that is centered around t is given by:
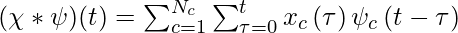
Now for continuous kernel convolution, we will use a convolution kernel ψ as continuous function parameterized over a small NN called MLPψ. It takes (t−τ ) as input and outputs the value of the convolution kernel at that position ψ(t−τ ). The continuous kernel can be formulated by:
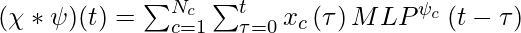
If the sampling factor is different from training sampling factor, then we can perform convolution operation in following ways:
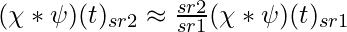
Recurrent Unit
For the input sequence
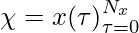 . The recurrent unit is given by:
. The recurrent unit is given by:
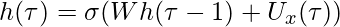
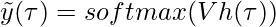
where U, W, V are the input-to-hidden, hidden-to-hidden and hidden-to-output connections of the unit. h(τ ), y˜(τ ) depict the hidden representation and the output at time-step τ, and σ represents a point-wise non-linearity.
Now, we unroll the above equation for t steps:
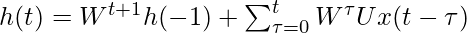
where h(−1) is the initial state of the hidden representation. h(t) can also be represented in following way:
![Rendered by QuickLaTeX.com x =[x(0), x(1), x(2) .....x(t-1),x(t)] \\ \psi =[U, WU, .... W^{t-1}U, W^{t}U] \\ h(t) = \sum_{\tau =0 }^{t}x(\tau)\psi(t-\tau) + \sum_{\tau =0 }^{t}x(t - \tau)\psi(\tau)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52d50198abfd2b59143f3b39b46ab9a6_l3.png)
The above equation provides us with following conclusion:
- Vanishing gradient and exploding gradient problem in RNN is caused by the term x(t-τ) τ steps back in the past being multiplied with an effective convolution weight ψ(τ )=WτU.
- Linear recurrent unit can be defined as the convolution of input and exponential convolution functions.
MLP Continuous Kernel
Let {∆ti=(t − τi)}N i=0 be a sequence of relative positions. The convolution kernel MLPψ is parameterized by a conventional L-layer neural network:
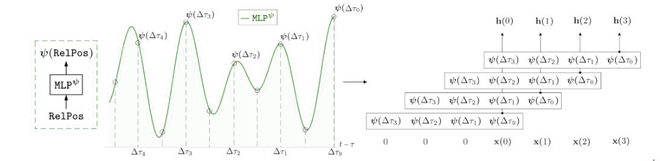
MLP
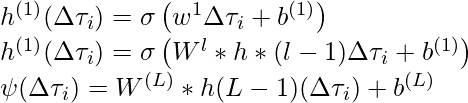
where,
 is used to add non-linearity such as ReLU.
is used to add non-linearity such as ReLU.
Implementation
- In this implementation, we will be training the CKconv model on the sMNIST dataset, for this implementation, we will be using colaboratory that is provided to us by Google.
Python3
! git clone https://github.com/dwromero/ckconv
cd ckconv
! pip install -r requirements.txt
pip install ml-collections torchaudio mkl-random sktime wandb
! python run_experiment.py --config.batch_size=64 --config.clip=0 \
--config.dataset=MNIST --config.device=cuda --config.dropout=0.1 \
--config.dropout_in=0.1 --config.epochs=200 --config.kernelnet_activation_function=Sine \
--config.kernelnet_no_hidden=32 --config.kernelnet_norm_type=LayerNorm \
--config.kernelnet_omega_0=31.09195739463897 --config.lr=0.001 --config.model=CKCNN \
--config.no_blocks=2 --config.no_hidden=30 --config.optimizer=Adam \
--config.permuted=False --config.sched_decay_factor=5 --config.sched_patience=20 \
--config.scheduler=plateau
|
- Below are the results of the above training of CKCNN on sMNIST data:
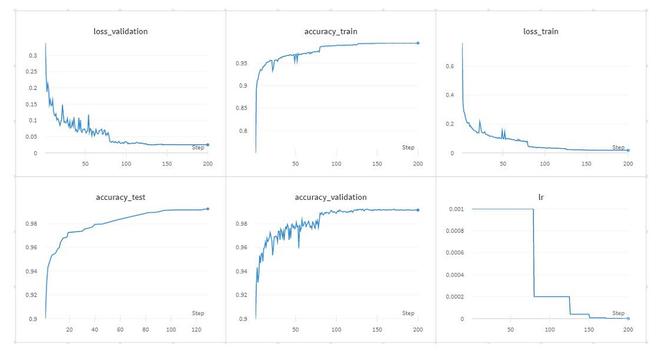
CkConv training Result
Conclusion
- Ckconv is able to very complex and non-linear function easily.
- Contrary to RNNs, CKConvs do not rely on any form of recurrence for considering large memory horizons and have global long-term dependencies.
- CKCNNs do not make use of Back-Propagation Through Time(BPTT). Consequently, CKCNNs can be trained in parallel.
- CKCNNs can also be deployed at resolutions other than the resolution on which it is trained.
References:
Share your thoughts in the comments
Please Login to comment...