Construct a Turing Machine for language L = {a^n b^m c^nm where n >=0 and m >= 0}
Last Updated :
24 Aug, 2022
Prerequisite – Turing Machine The language L = {anbmcnm | n >= 0 and m>=0} represents a kind of language where we use only 3 symbols, i.e., a, b and c. In the beginning, language has n number of a’s followed by m number of b’s and then n*m number of c’s. Any such string which falls in this category will be accepted by this language.
Examples:
Input : abbcc
Output : YES
Input : abbbcc
Output : NO
Input :  or empty stringOutput : YES
or empty stringOutput : YES
The basic Representation is as follows:
Start of Computation : The tape contains the input string w, the tape head is on the leftmost symbol of w, and the Turing machine is in the start state Q0.
Basic Idea : The tape head reads the leftmost symbol of w, which is a and at start only we will make it Blank. Then we will traverse to make leftmost b a $ and replace rightmost c by a Blank, we will do this zigzag pattern of replacing b by $ and c by Blank till all b are not replaced by $.After this we will traverse back in left direction till we get leftmost a and replacing all $ by b in the traversal. After this we have reduced our string into form an-1bmcnm-m so we can figure if all a’s are replaced by blankand if the string belongs to Language L then there will be no c’s left hence it will get accepted.
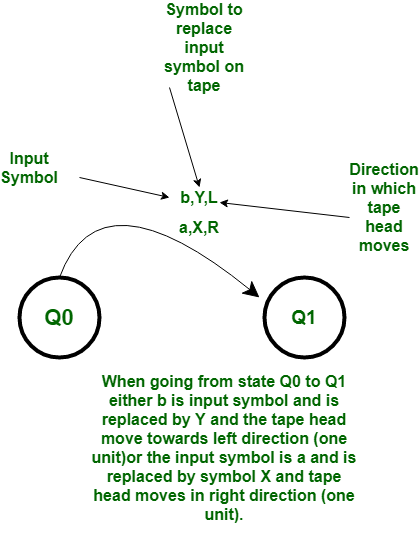
Meanings of symbols used: R, L – direction of movement of one unit on either side. B-Blank, a, b, c -symbols whose combination string is to be tested. $-Temporarily symbol to replace b.
Working Procedure :
- Step-1: We first replace leftmost a by Blank and then traverse to replace leftmost b by $ and rightmost c by Blank.Repeat this step from state Q1 till there is no more b left.
- Step-2: After replacing all b by $ we have also replaced m rightmost c’s with Blanks and then we will traverse back to left most a and replace all $ by b’s.After this step if check the string it is now reduced to an-1bmcnm-m form.
- Now we will repeat from step 1 till all a’s are not made Blank, but after all c’s are made blank, we encounter a Blank (B) at state Q1 which we keep as it is and go to the left most blank
- Step-4: So after all a’s are made blank and if the string belonged to Language L then 0 c’s must be left which we check at state Q0 and Q6 as only b’s will be left and after which if Blank is found then all c’s must have been replace by Blank as we where making c’s Blank from rightmost end of the string.
- Step-5: So if we get a Blank symbol at state Q6 the string is accepted at final state Q7. Also if the string was empty then it will also be accepted as Blank symbol input at state Q0 then it will got to state Q7 and gets accepted.
Share your thoughts in the comments
Please Login to comment...