Construct a Turing machine for L = {aibjck | i< j< k; i ≥ 1}
Last Updated :
23 Apr, 2019
Prerequisite – Turing Machine
In given language L = {aibjck | i< j< k; i≥ 1}, every string of ‘a’, ‘b’ and ‘c’ have certain number of a’s, then certain number of b’s and then certain number of c’s. The condition is that count of 1st symbols should be atleast 1. ‘b’ and ‘c’ can have thereafter be as many but count of a is less than count of ‘b’ and count of ‘b’ is less than count of ‘c’. Assume that string is ending with ‘$’.
Examples:
Input: a a a b b c
Here a = 3, b = 2, c = 1 but |a|<|b|<|c|
Output: NOT ACCEPTED
Input: a b b c c c
Here a = 1, b = 2, c = 3
Output:ACCEPTED
Tape Representation:

Approach:
- Comparing two elements by making D & C as a single element.
- After that Comparing D & C.
- If |A| is greater than |(D, C)|, then it is not accepted.
- If |C| is greater than |D|, then it is not accepted.
- Else it is accepted.
Steps:
- Step-1: Convert A into X and move right and goto step 2.If Y is found ignore it and move right to step-5.
- Step-2: Keep ignoring A and Y and move towards right. Convert D into Y and move right and goto step-3.
- Step-3: Keep ignoring D and Z and move towards right.If C is found make it Z and move left to step 4.
- Step-4: Keep ignoring Z, A, Y and D and move towards left.If X is found ignore it and move right and goto step-1.
- Step-5: Keep ignoring Y and move towards right. Ignore Z move left and goto step-8.If D is found make it Y and move right to step-6.
- Step-6: Keep ignoring D and Z and move towards right.Convert C into Z and move left and goto step-7.
- Step-7: Keep ignoring D and Z and move towards left.If Y is found ignore it and move right and goto step-5.
- Step-8: Stop the Machine (String is accepted)
State transition diagram :
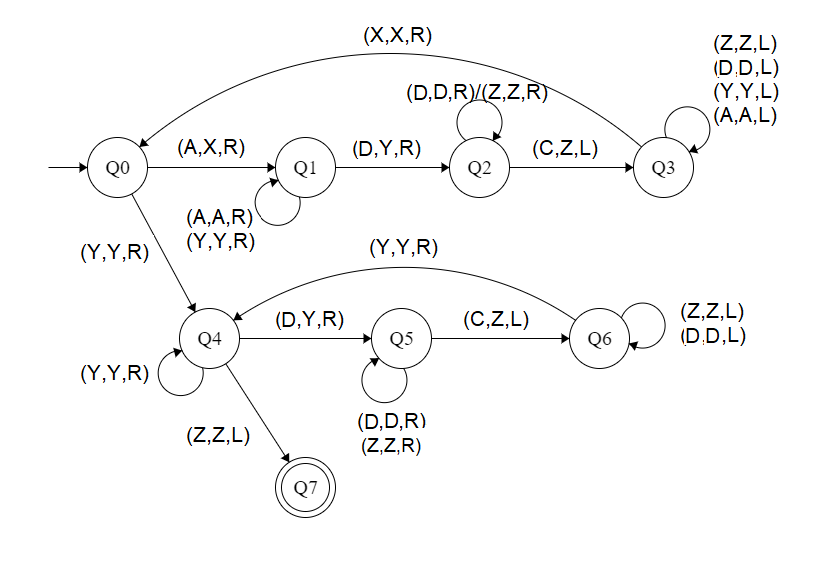
Here, Q0 shows the initial state and Q1, Q2, Q3, Q4, Q5, Q6 shows the transition state and Q7 shows the final state. A, C, D are the variables used and R, L shows right and left.
Explanation:
- Using Q0, when A is found make it X and go to the right and to state Q1. And, when Y is found ignore it and go to the right and to state Q4
- On the state Q1, ignore all A and Y and goto right. If D found, make it Y and goto right into next state Q2.
- In Q2, ignore all D, Z and move right. If C found, make it Z move left and to Q3.
- In Q3 state, ignore all Z, D, Y, A and move left. If X found, ignore it move right to Q0.
- In Q4, ignore all Y and move right. If Z found, ignore it move left to state Q6. If D is found, make it Y and move to the right to Q5.
- In Q5 state, ignore all D, Z and move right. If C found, make it Z move left to state Q6
- In Q6, ignore all D, Z and move left. If Y found, ignore it and move right to state Q4.
- If Q7 state is reached it will produce the result of the acceptance of string.
Note: For comparison of |A|, |D|, |C|, the concept of Turing Machine as Comparator is used.
Share your thoughts in the comments
Please Login to comment...