Class 9 RD Sharma Solutions – Chapter 24 Measures of Central Tendency – Exercise 24.2
Last Updated :
18 Mar, 2021
Question 1. Calculate the mean for the following distribution:
Solution:
| x | f | fx |
| 5 | 4 | 20 |
| 6 | 8 | 48 |
| 7 | 14 | 98 |
| 8 | 11 | 88 |
| 9 | 3 | 27 |
| | N = 40 | 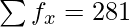 |
Now, mean = 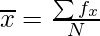
= 281/40
= 7.025
Question 2. Calculate the mean for the following distribution:
| x: | 19 | 21 | 23 | 25 | 27 | 29 | 31 |
| f: | 13 | 15 | 16 | 18 | 16 | 15 | 13 |
Solution:
| x | f | fx |
| 19 | 13 | 247 |
| 21 | 15 | 315 |
| 23 | 16 | 368 |
| 25 | 18 | 450 |
| 27 | 16 | 432 |
| 29 | 15 | 435 |
| 31 | 13 | 403 |
| | N = 106 | 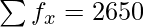 |
Now, mean = 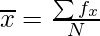
= 2650/106
= 25
Question 3. The mean of the following data is 20.6. Find the value of p.
Solution:
| x | f | fx |
| 10 | 3 | 30 |
| 15 | 10 | 150 |
| p | 25 | 25p |
| 25 | 7 | 175 |
| 35 | 5 | 175 |
| | N = 50 | 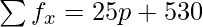 |
Now, mean = 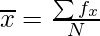
= (25p + 530)/50
Given,
Mean = 20.6
Solving, we get,
20.6 = (25p + 530)/50
25p + 530 = 1030
25p = 1030 − 530 = 500
that is, p = 20
Question 4. If the mean of the following data is 15, find p.
Solution:
| x | f | fx |
| 5 | 6 | 30 |
| 10 | p | 10p |
| 15 | 6 | 90 |
| 20 | 10 | 200 |
| 25 | 5 | 125 |
| | N = p+27 | 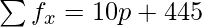 |
Mean = 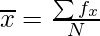
= (10p + 445)/(p + 27)
Give,
Mean = 15
Solving, (10p + 445)/(p + 27) = 15
10p + 445 = 15(p + 27)
10p – 15p = 405 – 445 = -40
-5p = -40
that is, p = 8
Question 5. Find the value of p for the following distribution whose mean is 16.6.
| x: | 8 | 12 | 15 | p | 20 | 25 | 30 |
| f: | 12 | 16 | 20 | 24 | 16 | 8 | 4 |
Solution:
| x | f | fx |
| 8 | 12 | 96 |
| 12 | 16 | 192 |
| 15 | 20 | 300 |
| p | 24 | 24p |
| 20 | 16 | 320 |
| 25 | 8 | 200 |
| 30 | 4 | 120 |
| | N = 100 | 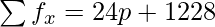 |
Now, mean = 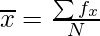
= (24p + 1228)/100
Given,
Mean = 16.6
Solving, (24p + 1228)/100 = 16.6
24p + 1228 = 1660
24p = 1660 – 1228 = 432
p = 432/24
= 18
Question 6. Find the missing value of p for the following distribution whose mean is 12.58.
Solution:
| x | f | fx |
| 5 | 2 | 10 |
| 8 | 5 | 40 |
| 10 | 8 | 80 |
| 12 | 22 | 264 |
| p | 7 | 7p |
| 20 | 4 | 80 |
| 25 | 2 | 50 |
| | N = 50 | 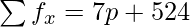 |
Mean = 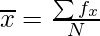
= (7p + 524)/50
Given,
Mean = 12.58
Solving, (7p + 524)/50 = 12.58
7p + 524 = 12.58 x 50
7p + 524 = 629
7p = 629 – 524 = 105
p = 105/7
= 15
Question 7. Find the missing frequency (p) for the following distribution whose mean is 7.68.
Solution:
| x | f | fx |
| 3 | 6 | 18 |
| 5 | 8 | 40 |
| 7 | 15 | 105 |
| 9 | p | 9p |
| 11 | 8 | 88 |
| 13 | 4 | 52 |
| | N = p +41 | 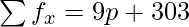 |
Mean = 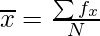
= (9p + 303)/(p+41)
Given,
Mean = 7.68
Solving we get, (9p + 303)/(p+41) = 7.68
9p + 303 = 7.68 (p + 41)
9p + 303 = 7.68p + 314.88
9p − 7.68p = 314.88 − 303
1.32p = 11.88
that is, p = (11.881)/(1.32) = 9
Question 8. Find the missing value of p for the following distribution whose mean is 12.58.
Solution:
| x | f | fx |
| 5 | 2 | 10 |
| 8 | 5 | 40 |
| 10 | 8 | 80 |
| 12 | 22 | 264 |
| p | 7 | 7p |
| 20 | 4 | 80 |
| 25 | 2 | 50 |
| | N = 50 | 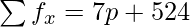 |
Given,
Mean = 12.58
=> 7p + 524/50 = 12.58
=> 7p + 524 = 629
=> 7p = 629 – 524
Solving for p, we get,
=> 7p = 105
that is, p = 105/7 = 15
Question 9. Find the missing frequency (p) for the following distribution whose mean is 7.68.
Solution:
| x | f | fx |
| 3 | 6 | 18 |
| 5 | 8 | 40 |
| 7 | 15 | 105 |
| 9 | p | 9p |
| 11 | 8 | 88 |
| 13 | 4 | 52 |
| | N = p + 41 | 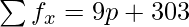 |
Mean = 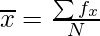
Given,
Mean = 7.68
Now,
9p + 303/ (p +41) = 7.68
Solving, we get,
9p + 303 = 7.68 + 314.88
9p-7.68p = 314.88 – 303
1.32p = 11.88
p = 9
Question 10. Find the value of p, if the mean of the following distribution is 20.
Solution:
| x | f | fx |
| 15 | 2 | 30 |
| 17 | 3 | 51 |
| 19 | 4 | 76 |
| 20+p | 5p | 100p+5p2 |
| 23 | 6 | 138 |
| | N = 15+5p | 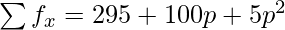 |
Given,
Mean = 20
Mean = 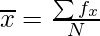
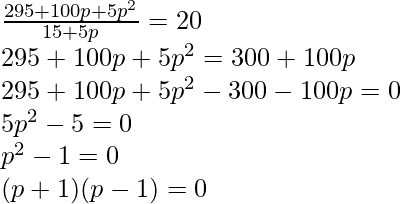
If p+1 = 0 or p-1 =0
p=-1
Question 11. Candidates of four schools appear in a mathematics test. The data were as follows:
| Schools | No. of Candidates | Average Score |
| I | 60 | 75 |
| II | 48 | 80 |
| III | Not available | 55 |
| IV | 40 | 50 |
If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:
Let us assume the number of candidates in school III to be p.
Therefore,
Total number of candidates in all the four schools = 60 + 48 + p + 40 = 148 + p
Average score of four schools = 66
∴Computing total score of the candidates = (148 + p) x 66
Now,
The mean score of 60 in school I is equivalent to 75 .
Total in school I = 60 x 75 = 4500
The mean score of 48 in school II is equivalent to 80 .
Total in school II = 48 x 80 = 3840
In school III, mean of p = 55
Total in school III= 55 x p = 55p
and in school IV, mean of 40 = 50
Total in school IV = 40 x 50 = 2000
Since, total of the candidates is 148+p.
Also,
Total score = 4500 + 3840 + 55p + 2000 = 10340 + 55p
∴10340 + 55p = (148 + p) x 66 = 9768 + 66p
=> 10340 – 9768 = 66p – 55p
=> 572 = 11p
∴ p = 572/11
Therefore,
The number of candidates in school III = 52
Question 12. Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.
| x: | 10 | 30 | 50 | 70 | 90 | |
| f: | 17 | f1 | 32 | f2 | 19 | Total = 120 |
Solution:
| x | f | fx |
| 10 | 17 | 170 |
| 30 | f1 | 30f1 |
| 50 | 32 | 1600 |
| 70 | f2 | 70f2 |
| 90 | 19 | 1710 |
| | N = 120 | 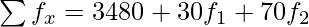 |
Given,
Mean = 50
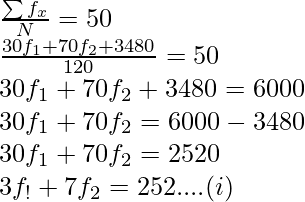
And, given value of N = 120
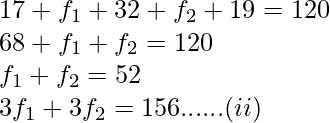
Subtracting (ii) from (i) ,
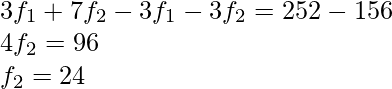
Substituting f2 in (i)
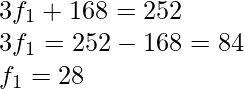
Share your thoughts in the comments
Please Login to comment...