Class 12 NCERT Solutions- Mathematics Part I – Chapter 5 Continuity And Differentiability – Exercise 5.7
Last Updated :
18 Mar, 2021
Find the second order derivatives of the functions given in Exercises 1 to 10.
Question 1. x2+ 3x + 2
Solution:
Here, y = x2+ 3x + 2
First derivative,
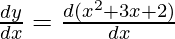
= 2x+ 3
Second derivative,
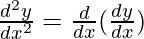
= 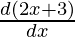
= 2
Question 2. x20
Solution:
Here, y = x20
First derivative,
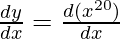
= 20x20-1
= 20x19
Second derivative,
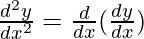
= 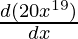
= 20(19x19-1)
= 380x18
Question 3. x . cos x
Solution:
Here, y = x . cos x
First derivative,
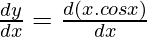
Using product rule
= x 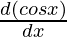 + cos x
+ cos x 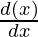
= x (-sin x)+ cos x (1)
= – x sin x+ cos x
Second derivative,
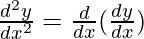
= 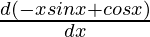
= 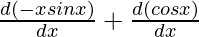
Using product rule,
= -x 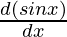 + sin x
+ sin x 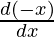 + (- sin x)
+ (- sin x)
= -x (cos x) + sin x (-1) – sin x
= – ( x cos x + 2 sin x)
Question 4. log x
Solution:
Here, y = log x
First derivative,

= 1/x
Second derivative,
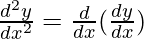
= 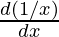
Using division rule,
=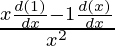
= 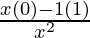
= 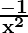
Question 5. x3 log x
Solution:
Here, y = x3 . log x
First derivative,
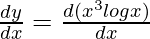
Using product rule
= x3 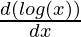 + log x
+ log x 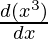
= x3 (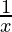 ) + log x (3x2)
) + log x (3x2)
= x2 + 3x2 log x
Second derivative,
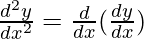
= 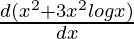
= 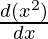 +
+ 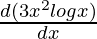
Using product rule,
= 2x + 3 (x2 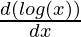 – log x
– log x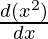 )
)
= 2x + 3 (x2 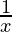 – log x (2x))
– log x (2x))
= 2x + 3 (x – 2x . log x)
= 2x + 3x – 6x . log x
= x(5 – 6 log x)
Question 6. ex sin 5x
Solution:
Here, y = ex sin 5x
First derivative,
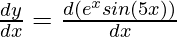
Using product rule
= ex 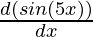 + sin 5x
+ sin 5x 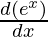
= ex (5 cos(5x))+ sin 5x (ex)
= ex (5 cos(5x)+ sin 5x)
Second derivative,
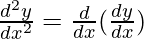
=
Using product rule,
= ex 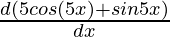 + (5 cos(5x)+ sin 5x)
+ (5 cos(5x)+ sin 5x) 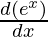
= ex (5 (5(- sin 5x))) + 5(cos 5x) + (5 cos(5x)+ sin 5x) (ex)
= ex (- 25 sin 5x + 5cos 5x) + (5 cos(5x)+ sin 5x) (ex)
= ex (- 25 sin 5x + 5cos 5x + 5 cos(5x)+ sin 5x)
= ex (10 cos 5x – 24 sin 5x)
Question 7. e6x cos 3x
Solution:
Here, y = e6x cos 3x
First derivative,

Using product rule
= e6x  + cos 3x
+ cos 3x 
= e6x (- 3 sin(3x))+ cos 3x (6e6x)
= e6x (6 cos(3x) – 3 sin (3x))
Second derivative,
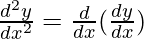
= 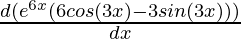
Using product rule,
= e6x (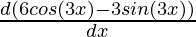 ) + (6 cos(3x) – 3 sin (3x))
) + (6 cos(3x) – 3 sin (3x)) 
= e6x (6 (3 (- sin(3x)) – 3 (3 cos 3x)) + (6 cos(3x) – 3 sin (3x)) (6e6x)
= e6x (- 18sin(3x) – 9 cos 3x) + (36 cos(3x) – 18 sin (3x)) (e6x)
= e6x (27 cos(3x) – 36 sin (3x))
= 9e6x (3 cos(3x) – 4 sin (3x))
Question 8. tan–1 x
Solution:
Here, y = tan–1 x
First derivative,
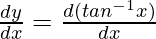
= 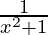
Second derivative,
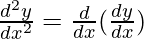
= 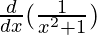
Using division rule,
=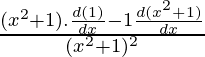
= 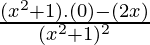
= 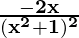
Question 9. log (log x)
Solution:
Here, y = log (log x)
First derivative,
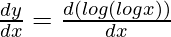
= 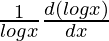
= 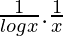
= 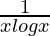
Second derivative,
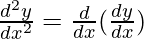
=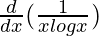
Using division rule,
= 
Using product rule,
= 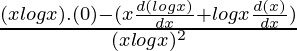
= – 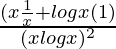
= – 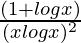
= – 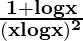
Question 10. sin (log x)
Solution:
Here, y = sin (log x)
First derivative,
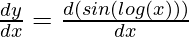
= cos (log x) 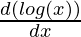
= cos (log x) . 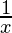
= 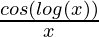
Second derivative,
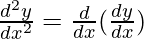
= 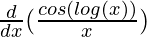
Using division rule,
= 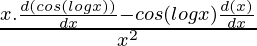
= 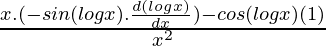
= 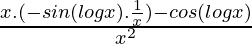
= 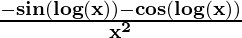
Question 11. If y = 5 cos x – 3 sin x, prove that 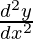 + y = 0
+ y = 0
Solution:
Here, y = 5 cos x – 3 sin x
First derivative,
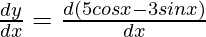
= 5 (- sin x) – 3 (cos x)
= – 5 sin(x) – 3 cos(x)
Second derivative,
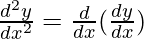
= 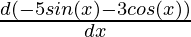
= 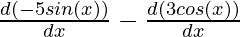
= -5 (cos(x)) – 3 (- sin(x))
= -(5 cos(x) – 3 sin(x))
= -y
According to the given condition,
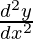 + y = -y + y
+ y = -y + y
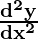 + y = 0
+ y = 0
Hence Proved!!
Question 12. If y = cos-1 x, Find 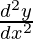 in terms of y alone.
in terms of y alone.
Solution:
Here, y = cos-1 x
x = cos y
First derivative,
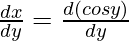
= – sin y
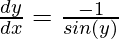
= – cosec (y)
Second derivative,
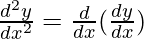
= 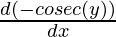
= – (-cosec(y) cot (y)) 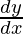
= – (-cosec(y) cot (y)) (-cosec(y))
= -cosec2(y) cot (y)
Hence we get
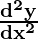 = -cosec2(y) cot (y)
= -cosec2(y) cot (y)
Question 13. If y = 3 cos (log x) + 4 sin (log x), show that x2 y2+ xy1+ y = 0
Solution:
Here, y = 3 cos (log x) + 4 sin (log x)
First derivative,
y1 = 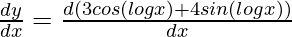
= 3 (-sin (log x)) 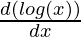 + 4 (cos (log(x)))
+ 4 (cos (log(x))) 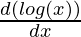
= 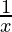 (4 cos (log(x)-3 sin (log x))
(4 cos (log(x)-3 sin (log x))
Second derivative,
y2 = 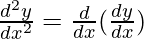
= 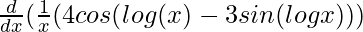
Using product rule.
= 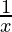

= 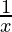 (4(-sin(log(x)))
(4(-sin(log(x)))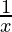 – 3 (cos(log(x)))
– 3 (cos(log(x)))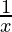 ) + (4 cos (log(x)-3 sin (log x)) (
) + (4 cos (log(x)-3 sin (log x)) (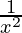 )
)
= 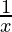 (-4sin(log(x))
(-4sin(log(x))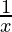 – 3 cos(log(x))
– 3 cos(log(x))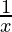 ) – (4 cos (log(x) + 3 sin (log x)) (
) – (4 cos (log(x) + 3 sin (log x)) (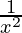 )
)
= \frac{-1}{x^2} [-7 cos(log(x) – sin (log x)]
According to the given conditions,
xy1 = x(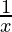 (4 cos (log(x)-3 sin (log x)))
(4 cos (log(x)-3 sin (log x)))
xy1 = -3 sin (log x)+ 4 cos (log(x))
x2 y2 = x2 ![Rendered by QuickLaTeX.com (\frac{1}{x^2} [-7 cos(log(x) - sin (log x)])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4eae822528baecc3985222c0f52f9b71_l3.png)
x2 y2 =[-7 cos(log(x) – sin (log x)]
Now, rearranging
xy1 + x2 y2 + y = -3 sin (log x)+ 4 cos (log(x)) + cos(log(x)) -7 cos(log(x) – sin (log x) + 4 sin (log x)
Hence we get
xy1 + x2 y2 + y = 0
Question 14. If y = Aemx + Benx, show that 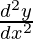 – (m+n)
– (m+n)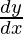 + mny = 0.
+ mny = 0.
Solution:
Here, y = Aemx + Benx
First derivative,
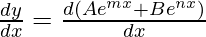
= mAemx + nBenx
Second derivative,
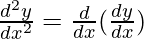
= 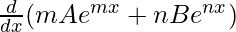
= m2Aemx + n2Benx
According to the given conditions,
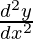 – (m+n)
– (m+n) 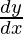 + mny, we get
+ mny, we get
LHS = m2Aemx + n2Benx – (m+n)(mAemx + nBenx) + mny
= m2Aemx + n2Benx – (m2Aemx + mnAemx + mnBenx + n2Benx) + mny
= -(mnAemx + mnBenx) + mny
= -mny + mny
= 0
Hence we get
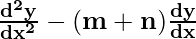 + mny = 0
+ mny = 0
Question 15. If y = 500e7x+ 600e– 7x, show that 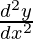 = 49y.
= 49y.
Solution:
Here, y = 500e7x+ 600e– 7x
First derivative,

= 500e7x . (7)+ 600e– 7x (-7)
= 7(500e7x – 600e– 7x)
Second derivative,
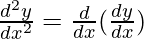
= 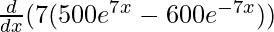
= 7[500e7x . (7) – 600e– 7x . (-7)]
= 49[500e7x + 600e– 7x]
= 49y
Hence Proved!!
Question 16. If ey (x + 1) = 1, show that 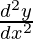 =
= 
Solution:
ey (x + 1) = 1
e-y = (x+1)
First derivative,
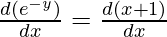
-e-y 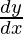 = 1
= 1
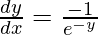
= 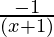
Second derivative,
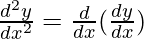
= 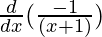
Using division rule,
= 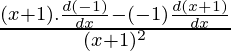
= 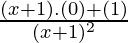
= 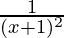
= 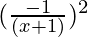
Hence we can conclude that,

Question 17. If y = (tan–1 x)2, show that (x2+ 1)2 y2+ 2x (x2+ 1) y1= 2
Solution:
Here, y = (tan–1 x)2
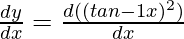
= 2 . tan–1 x 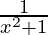
(x2 + 1) 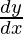 = 2 tan–1 x
= 2 tan–1 x
Derivation further,
(x2 + 1)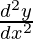 +
+ 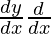 (x2 + 1) =
(x2 + 1) = 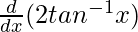
(x2 + 1)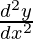 +
+ 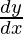 (2x) = 2
(2x) = 2 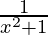
Multiplying (x2 + 1),
(x2 + 1)2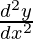 +
+ 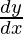 (2x)(x2 + 1) = 2
(2x)(x2 + 1) = 2
Hence Proved,
(x2+ 1)2 y2+ 2x (x2+ 1) y1= 2
Share your thoughts in the comments
Please Login to comment...