Question 1. Prove that the function f(x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
Solution:
To prove the continuity of the function f(x) = 5x – 3, first we have to calculate limits and function value at that point.
Continuity at x = 0
Left limit = 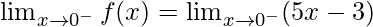
= (5(0) – 3) = -3
Right limit = 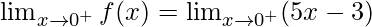
= (5(0) – 3)= -3
Function value at x = 0, f(0) = 5(0) – 3 = -3
As, 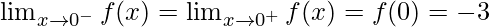 ,
,
Hence, the function is continuous at x = 0.
Continuity at x = -3
Left limit = 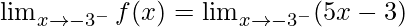
= (5(-3) – 3) = -18
Right limit = 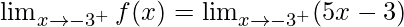
= (5(-3) – 3) = -18
Function value at x = -3, f(-3) = 5(-3) – 3 = -18
As, 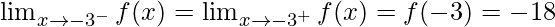
Hence, the function is continuous at x = -3.
Continuity at x = 5
Left limit = 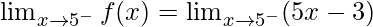
= (5(5) – 3) = 22
Right limit = 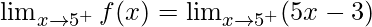
= (5(5) – 3) = 22
Function value at x = 5, f(5) = 5(5) – 3 = 22
As, 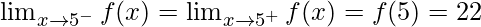
Hence, the function is continuous at x = 5.
Question 2. Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Solution:
To prove the continuity of the function f(x) = 2x2 – 1, first we have to calculate limits and function value at that point.
Continuity at x = 3
Left limit = 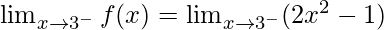
= (2(3)2 – 1) = 17
Right limit = 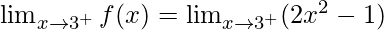
= (2(3)2 – 1) = 17
Function value at x = 3, f(3) = 2(3)2 – 1 = 17
As, 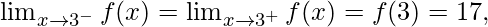
Hence, the function is continuous at x = 3.
Question 3. Examine the following functions for continuity.
(a) f(x) = x – 5
Solution:
To prove the continuity of the function f(x) = x – 5, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c
Left limit = 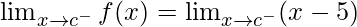
= (c – 5) = c – 5
Right limit = 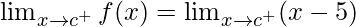
= (c – 5) = c – 5
Function value at x = c, f(c) = c – 5
As, 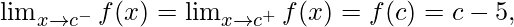 for any real number c
for any real number c
Hence, the function is continuous at every real number.
(b) 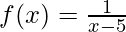 , x ≠ 5
, x ≠ 5
Solution:
To prove the continuity of the function f(x) = 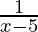 , first we have to calculate limits and function value at that point.
, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c and c ≠ 5
Left limit = 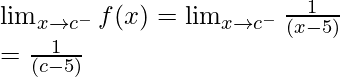
Right limit = 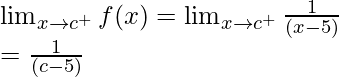
Function value at x = c, f(c) = 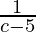
As, 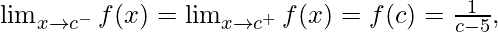 for any real number c
for any real number c
Hence, the function is continuous at every real number.
(c) 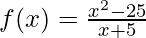 , x ≠ -5
, x ≠ -5
Solution:
To prove the continuity of the function f(x) = 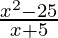 , first we have to calculate limits and function value at that point.
, first we have to calculate limits and function value at that point.
Let’s take a real number, c
Continuity at x = c and c ≠ -5
Left limit = 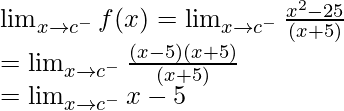
= c – 5
Right limit = 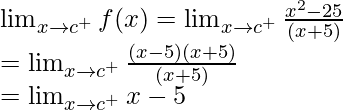
= c – 5
Function value at x = c, f(c) = 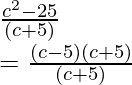
= c – 5
As, 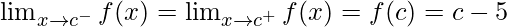 , for any real number c
, for any real number c
Hence, the function is continuous at every real number.
(d) f(x) = |x – 5|
Solution:
To prove the continuity of the function f(x) = |x – 5|, first we have to calculate limits and function value at that point.
Here,
As, we know that modulus function works differently.
In |x – 5|, |x – 5| = x – 5 when x>5 and |x – 5| = -(x – 5) when x < 5
Let’s take a real number, c and check for three cases of c:
Continuity at x = c
When c < 5
Left limit = 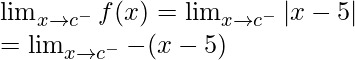
= -(c – 5)
= 5 – c
Right limit = 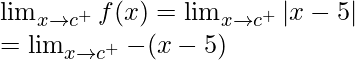
= -(c – 5)
= 5 – c
Function value at x = c, f(c) = |c – 5| = 5 – c
As, 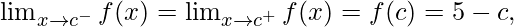
Hence, the function is continuous at every real number c, where c<5.
When c > 5
Left limit = 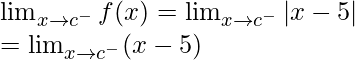
= (c – 5)
Right limit = 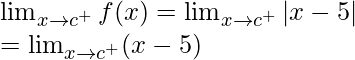
= (c – 5)
Function value at x = c, f(c) = |c – 5| = c – 5
As, 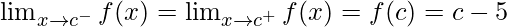 ,
,
Hence, the function is continuous at every real number c, where c > 5.
When c = 5
Left limit = 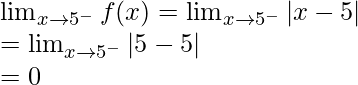
Right limit = 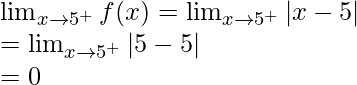
Function value at x = c, f(c) = |5 – 5| = 0
As, 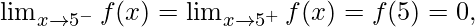
Hence, the function is continuous at every real number c, where c = 5.
Hence, we can conclude that, the modulus function is continuous at every real number.
Question 4. Prove that the function f(x) = xn is continuous at x = n, where n is a positive integer.
Solution:
To prove the continuity of the function f(x) = xn, first we have to calculate limits and function value at that point.
Continuity at x = n
Left limit = 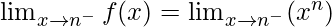
= nn
Right limit = 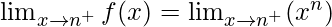
= nn
Function value at x = n, f(n) = nn
As, 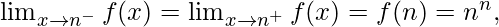
Hence, the function is continuous at x = n.
Question 5. Is the function f defined by
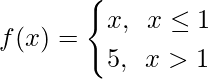
continuous at x = 0? At x = 1? At x = 2?
To prove the continuity of the function f(x), first we have to calculate limits and function value at that point.
Continuity at x = 0
Left limit = 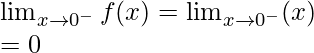
Right limit = 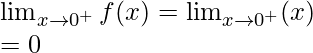
Function value at x = 0, f(0) = 0
As, 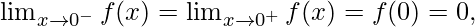
Hence, the function is continuous at x = 0.
Continuity at x = 1
Left limit = 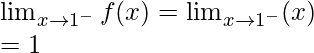
Right limit = 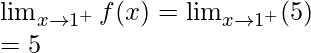
Function value at x = 1, f(1) = 1
As, 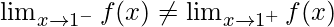 ,
,
Hence, the function is not continuous at x = 1.
Continuity at x = 2
Left limit = 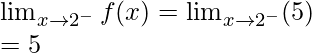
Right limit = 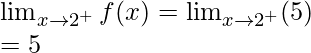
Function value at x = 2, f(2) = 5
As, 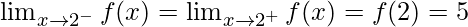 ,
,
Therefore, the function is continuous at x = 2.
Find all points of discontinuity of f, where f is defined by
Question 6. 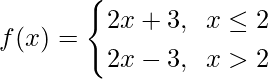
Solution:
Here, as it is given that
For x ≤ 2, f(x) = 2x + 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 2)
Now, For x > 2, f(x) = 2x – 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (2, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 2) U (2, ∞) = R – {2}
Let’s check the continuity at x = 2,
Left limit = 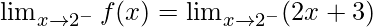
= (2(2) + 3)
= 7
Right limit = 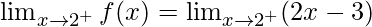
= (2(2) – 3)
= 1
Function value at x = 2, f(2) = 2(3) + 3 = 7
As, 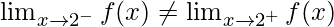
Therefore, the function is discontinuous at only x = 2.
Question 7. 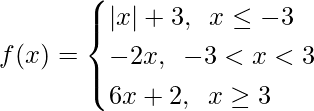
Solution:
Here, as it is given that
For x ≤ -3, f(x) = |x| + 3,
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0| = -x when x < 0
f(x) = -x + 3, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, -3)
For -3 < x < 3, f(x) = -2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-3, 3)
Now, for x ≥ 3, f(x) = 6x + 2, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (3, ∞)
So now, as f(x) is continuous in x ∈ (-∞, -3) U(-3, 3) U (3, ∞) = R – {-3, 3}
Let’s check the continuity at x = -3,
Left limit = 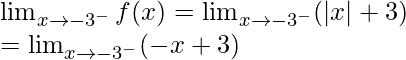
= (-(-3) + 3)
= 6
Right limit = 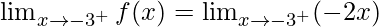
= (-2(-3))
= 6
Function value at x = -3, f(-3) = |-3| + 3 = 3 + 3 = 6
As, 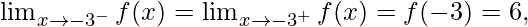
Hence, the function is continuous at x = -3.
Now, let’s check the continuity at x = 3,
Left limit = 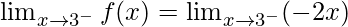
= (-2(3))
= -6
Right limit = 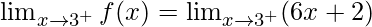
= (6(3) + 2)
= 20
Function value at x = 3, f(3) = 6(3) + 2 = 20
As, 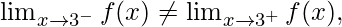
Therefore, the function is discontinuous only at x = 3.
Question 8. 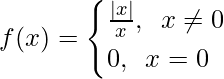
Solution:
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0|= -x when x < 0
When x < 0, f(x) = 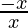 = -1, which is a constant
= -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (-∞, 0).
When x > 0, f(x) = 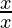 = 1, which is a constant
= 1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (0, ∞).
So now, as f(x) is continuous in x ∈ (-∞, 0) U(0, ∞) = R – {0}
Let’s check the continuity at x = 0,
Left limit = 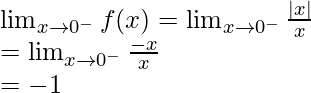
Right limit = 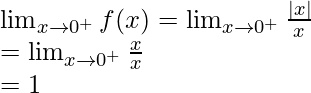
Function value at x = 0, f(0) = 0
As, 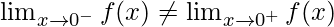
Hence, the function is discontinuous at only x = 0.
Question 9. 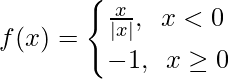
Solution:
As, we know that modulus function works differently.
In |x|, |x – 0| = x when x > 0 and |x – 0| = -x when x < 0
When x < 0, f(x) = 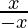 = -1, which is a constant
= -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (-∞, 0).
When x > 0, f(x) = -1, which is a constant
As constant functions are continuous, hence f(x) is continuous x ∈ (0, ∞).
So now, as f(x) is continuous in x ∈ (-∞, 0) U(0, ∞) = R – {0}
Let’s check the continuity at x = 0,
Left limit = 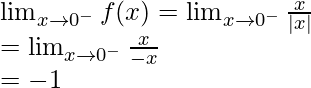
Right limit = 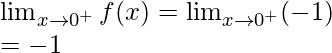
Function value at x = 0, f(0) = -1
As, 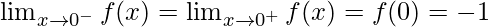
Hence, the function is continuous at x = 0.
So, we conclude that the f(x) is continuous at any real number. Hence, no point of discontinuity.
Question 10. 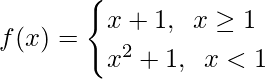
Solution:
Here,
When x ≥1, f(x) = x + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (1, ∞)
When x < 1, f(x) = x2 + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 1)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = 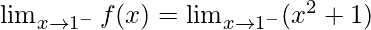
= 1 + 1
= 2
Right limit = 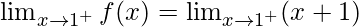
= 1 + 1
= 2
Function value at x = 1, f(1) = 1 + 1 = 2
As, 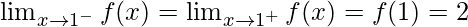
Hence, the function is continuous at x = 1.
So, we conclude that the f(x) is continuous at any real number.
Question 11. 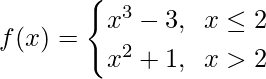
Solution:
Here,
When x ≤ 2, f(x) = x3 + 3, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 2)
When x > 2, f(x) = x2 + 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (2, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 2) U(2, ∞) = R – {2}
Let’s check the continuity at x = 2,
Left limit = 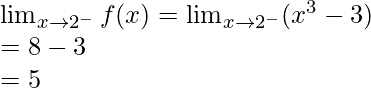
Right limit = 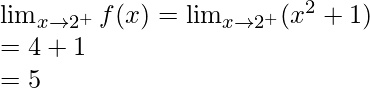
Function value at x = 2, f(2) = 8 – 3 = 5
As, 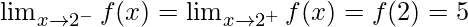
Hence, the function is continuous at x = 2.
So, we conclude that the f(x) is continuous at any real number.
Question 12. 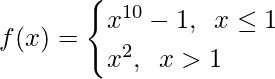
Solution:
Here,
When x ≤ 1, f(x) = x10 – 1, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (-∞, 1)
When x >1, f(x) = x2, which is a polynomial
As polynomial functions are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = 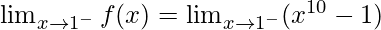
= 1 – 1
= 0
Right limit = 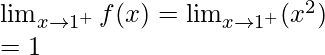
Function value at x = 1, f(1) = 1 – 1 = 0
As, 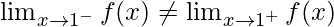
Hence, the function is discontinuous at x = 1.
Question 13. Is the function defined by
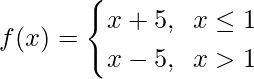
a continuous function?
Solution:
Here, as it is given that
For x ≤ 1, f(x) = x + 5, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 1)
Now, For x > 1, f(x) = x – 5, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 1) U (1, ∞) = R – {1}
Let’s check the continuity at x = 1,
Left limit = 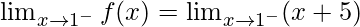
= (1 + 5)
= 6
Right limit = 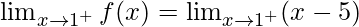
= (1 – 5)
= -4
Function value at x = 1, f(1) = 5 + 1 = 6
As, 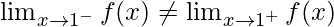
Hence, the function is continuous for only R – {1}.
Discuss the continuity of the function f, where f is defined by
Question 14. 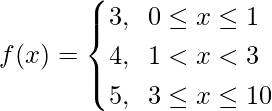
Solution:
Here, as it is given that
For 0 ≤ x ≤ 1, f(x) = 3, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (0, 1)
Now, For 1 < x < 3, f(x) = 4, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (1, 3)
For 3 ≤ x ≤ 10, f(x) = 5, which is a constant
As constants are continuous, hence f(x) is continuous x ∈ (3, 10)
So now, as f(x) is continuous in x ∈ (0, 1) U (1, 3) U (3, 10) = (0, 10) – {1, 3}
Let’s check the continuity at x = 1,
Left limit = 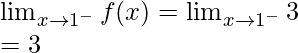
Right limit = 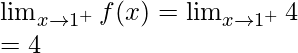
Function value at x = 1, f(1) = 3
As, 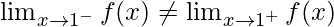
Hence, the function is discontinuous at x = 1.
Now, let’s check the continuity at x = 3,
Left limit = 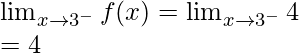
Right limit = 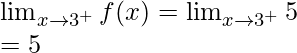
Function value at x = 3, f(3) = 4
As, 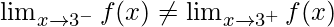
Hence, the function is discontinuous at x = 3.
So concluding the results, we get
Therefore, the function f(x) is discontinuous at x = 1 and x = 3.
Question 15. 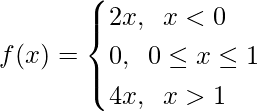
Solution:
Here, as it is given that
For x < 0, f(x) = 2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-∞, 0)
Now, For 0 ≤ x ≤ 1, f(x) = 0, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (0, 1)
For x > 1, f(x) = 4x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 0) U (0, 1) U (1, ∞)= R – {0, 1}
Let’s check the continuity at x = 0,
Left limit = 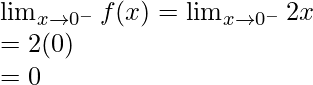
Right limit = 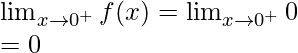
Function value at x = 0, f(0) = 0
As, 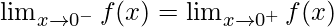
Hence, the function is continuous at x = 0.
Now, let’s check the continuity at x = 1,
Left limit = 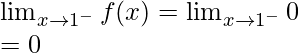
Right limit = 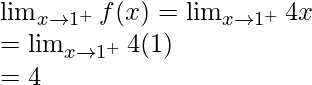
Function value at x = 1, f(1) = 0
As, 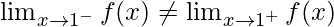
Hence, the function is discontinuous at x = 1.
Therefore, the function is continuous for only R – {1}
Question 16. 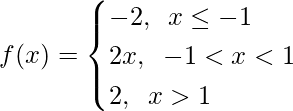
Solution:
Here, as it is given that
For x ≤ -1, f(x) = -2, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (-∞, -1)
Now, For -1 ≤ x ≤ 1, f(x) = 2x, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (-1, 1)
For x > 1, f(x) = 2, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ (1, ∞)
So now, as f(x) is continuous in x ∈ (-∞, -1) U (-1, 1) U (1, ∞)= R – {-1, 1}
Let’s check the continuity at x = -1,
Left limit = 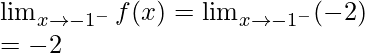
Right limit = 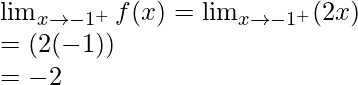
Function value at x = -1, f(-1) = -2
As, 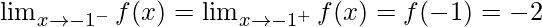
Hence, the function is continuous at x = -1.
Now, let’s check the continuity at x = 1,
Left limit = 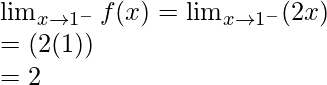
Right limit = 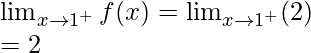
Function value at x = 1, f(1) = 2(1) = 2
As, 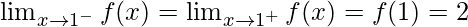
Hence, the function is continuous at x = 1.
Therefore, the function is continuous for any real number.
Question 17. Find the relationship between a and b so that the function f defined by
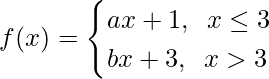
is continuous at x = 3.
Solution:
As, it is given that the function is continuous at x = 3.
It should satisfy the following at x = 3:
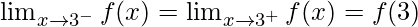
Continuity at x = 3,
Left limit = 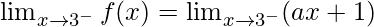
= (a(3) + 1)
= 3a + 1
Right limit = 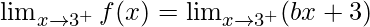
= (b(3) + 3)
= 3b + 3
Function value at x = 3, f(3) = a(3) + 1 = 3a + 1
So equating both the limits, we get
3a + 1 = 3b + 3
3(a – b) = 2
a – b = 2/3
Question 18. For what value of λ is the function defined by
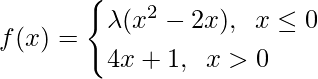
continuous at x = 0? What about continuity at x = 1?
Solution:
To be continuous function, f(x) should satisfy the following at x = 0:
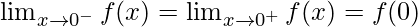
Continuity at x = 0,
Left limit = 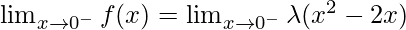
= λ(02– 2(0)) = 0
Right limit = 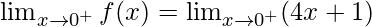
= λ4(0) + 1 = 1
Function value at x = 0, f(0) = 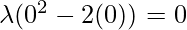
As, 0 = 1 cannot be possible
Hence, for no value of λ, f(x) is continuous.
But here, 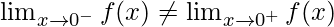
Continuity at x = 1,
Left limit = 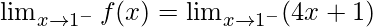
= (4(1) + 1) = 5
Right limit = 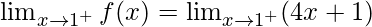
= 4(1) + 1 = 5
Function value at x = 1, f(1) = 4(1) + 1 = 5
As, 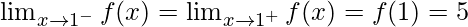
Hence, the function is continuous at x = 1 for any value of λ.
Question 19. Show that the function defined by g (x) = x – [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Solution:
[x] is greatest integer function which is defined in all integral points, e.g.
[2.5] = 2
[-1.96] = -2
x-[x] gives the fractional part of x.
e.g: 2.5 – 2 = 0.5
c be an integer
Let’s check the continuity at x = c,
Left limit = ![Rendered by QuickLaTeX.com \lim_{x \to c^-} f(x) = \lim_{x \to c^-} (x-[x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe136abd948a59b3d508886c7cd94236_l3.png)
= (c – (c – 1)) = 1
Right limit = ![Rendered by QuickLaTeX.com \lim_{x \to c^+} f(x) = \lim_{x \to c^+} (x-[x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-024a58c1f8b8beb895a2b35450359b0f_l3.png)
= (c – c) = 0
Function value at x = c, f(c) = c – = c – c = 0
As, 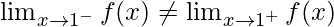
Hence, the function is discontinuous at integral.
c be not an integer
Let’s check the continuity at x = c,
Left limit = ![Rendered by QuickLaTeX.com \lim_{x \to c^-} f(x) = \lim_{x \to c^-} (x-[x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe136abd948a59b3d508886c7cd94236_l3.png)
= (c – (c – 1)) = 1
Right limit = ![Rendered by QuickLaTeX.com \lim_{x \to c^+} f(x) = \lim_{x \to c^+} (x-[x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-024a58c1f8b8beb895a2b35450359b0f_l3.png)
= (c – (c – 1)) = 1
Function value at x = c, f(c) = c – = c – (c – 1) = 1
As, 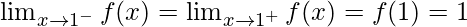
Hence, the function is continuous at non-integrals part.
Question 20. Is the function defined by f(x) = x2 – sin x + 5 continuous at x = π?
Solution:
Let’s check the continuity at x = π,
f(x) = x2 – sin x + 5
Let’s substitute, x = π+h
When x⇢π, Continuity at x = π
Left limit = 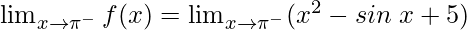
= (π2 – sinπ + 5) = π2 + 5
Right limit = 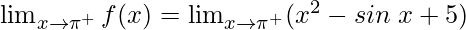
= (π2 – sinπ + 5) = π2 + 5
Function value at x = π, f(π) = π2 – sin π + 5 = π2 + 5
As, 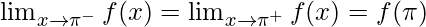
Hence, the function is continuous at x = π .
Question 21. Discuss the continuity of the following functions:
(a) f(x) = sin x + cos x
Solution:
Here,
f(x) = sin x + cos x
Let’s take, x = c + h
When x⇢c then h⇢0
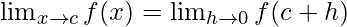
So,
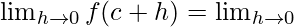 (sin(c + h) + cos(c + h))
(sin(c + h) + cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
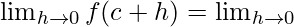 ((sinc cosh + cosc sinh) + (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) + (cosc cosh − sinc sinh))
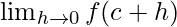 = ((sinc cos0 + cosc sin0) + (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) + (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
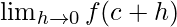 = (sinc + cosc) = f(c)
= (sinc + cosc) = f(c)
Function value at x = c, f(c) = sinc + cosc
As, 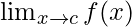 = f(c) = sinc + cosc
= f(c) = sinc + cosc
Hence, the function is continuous at x = c.
(b) f(x) = sin x – cos x
Solution:
Here,
f(x) = sin x – cos x
Let’s take, x = c+h
When x⇢c then h⇢0
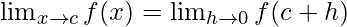
So,
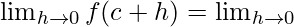 (sin(c + h) − cos(c + h))
(sin(c + h) − cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
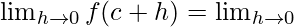 ((sinc cosh + cosc sinh) − (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) − (cosc cosh − sinc sinh))
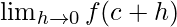 = ((sinc cos0 + cosc sin0) − (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) − (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
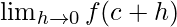 = (sinc − cosc) = f(c)
= (sinc − cosc) = f(c)
Function value at x = c, f(c) = sinc − cosc
As, 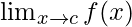 = f(c) = sinc − cosc
= f(c) = sinc − cosc
Hence, the function is continuous at x = c.
(c) f(x) = sin x . cos x
Solution:
Here,
f(x) = sin x + cos x
Let’s take, x = c+h
When x⇢c then h⇢0
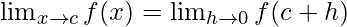
So,
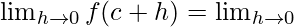 sin(c + h) × cos(c + h))
sin(c + h) × cos(c + h))
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
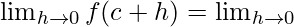 ((sinc cosh + cosc sinh) × (cosc cosh − sinc sinh))
((sinc cosh + cosc sinh) × (cosc cosh − sinc sinh))
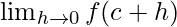 = ((sinc cos0 + cosc sin0) × (cosc cos0 − sinc sin0))
= ((sinc cos0 + cosc sin0) × (cosc cos0 − sinc sin0))
cos 0 = 1 and sin 0 = 0
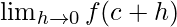 = (sinc × cosc) = f(c)
= (sinc × cosc) = f(c)
Function value at x = c, f(c) = sinc × cosc
As, 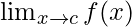 = f(c) = sinc × cosc
= f(c) = sinc × cosc
Hence, the function is continuous at x = c.
Question 22. Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Solution:
Continuity of cosine
Here,
f(x) = cos x
Let’s take, x = c+h
When x⇢c then h⇢0
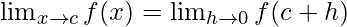
So,
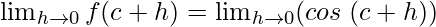
Using the trigonometric identities, we get
cos(A + B) = cos A cos B – sin A sin B
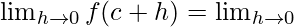 (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
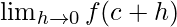 = (cosc cos0 − sinc sin0)
= (cosc cos0 − sinc sin0)
cos 0 = 1 and sin 0 = 0
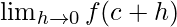 = (cosc) = f(c)
= (cosc) = f(c)
Function value at x = c, f(c) = (cosc)
As, 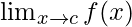 = f(c) = (cosc)
= f(c) = (cosc)
Hence, the cosine function is continuous at x = c.
Continuity of cosecant
Here,
f(x) = cosec x = 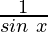
Domain of cosec is R – {nπ}, n ∈ Integer
Let’s take, x = c + h
When x⇢c then h⇢0
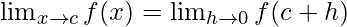
So,
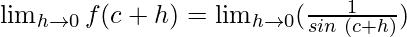
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
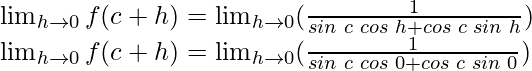
cos 0 = 1 and sin 0 = 0
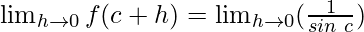
Function value at x = c, f(c) = 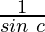
As, 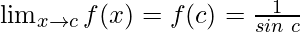
Hence, the cosecant function is continuous at x = c.
Continuity of secant
Here,
f(x) = sec x = 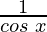
Let’s take, x = c + h
When x⇢c then h⇢0
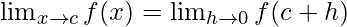
So,
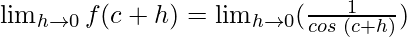
Using the trigonometric identities, we get
cos(A + B) = cos A cos B – sin A sin B
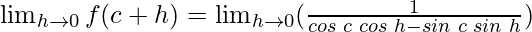
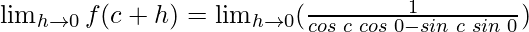
cos 0 = 1 and sin 0 = 0
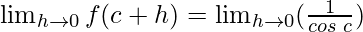
Function value at x = c, f(c) = 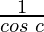
As, 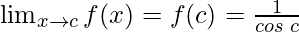
Hence, the secant function is continuous at x = c.
Continuity of cotangent
Here,
f(x) = cot x = 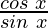
Let’s take, x = c+h
When x⇢c then h⇢0
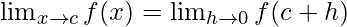
So,
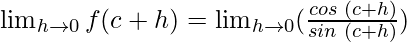
Using the trigonometric identities, we get
sin(A + B) = sin A cos B + cos A sin B
cos(A + B) = cos A cos B – sin A sin B
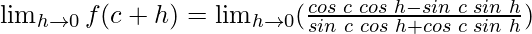
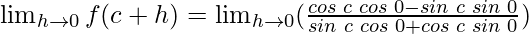
cos 0 = 1 and sin 0 = 0
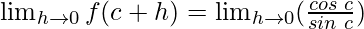
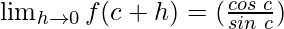
Function value at x = c, f(c) = 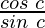
As, 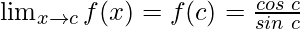
Hence, the cotangent function is continuous at x = c.
Question 23. Find all points of discontinuity of f, where
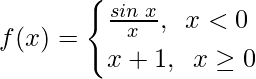
Solution:
Here,
From the two continuous functions g and h, we get
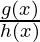 = continuous when h(x) ≠ 0
= continuous when h(x) ≠ 0
For x < 0, f(x) = 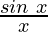 , is continuous
, is continuous
Hence, f(x) is continuous x ∈ (-∞, 0)
Now, For x ≥ 0, f(x) = x + 1, which is a polynomial
As polynomial are continuous, hence f(x) is continuous x ∈ (0, ∞)
So now, as f(x) is continuous in x ∈ (-∞, 0) U (0, ∞)= R – {0}
Let’s check the continuity at x = 0,
Left limit = 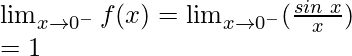
Right limit = 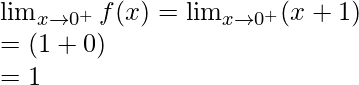
Function value at x = 0, f(0) = 0 + 1 = 1
As, 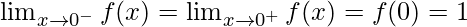
Hence, the function is continuous at x = 0.
Hence, the function is continuous for any real number.
Question 24. Determine if f defined by
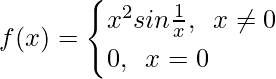
is a continuous function?
Solution:
Here, as it is given that
For x = 0, f(x) = 0, which is a constant
As constant are continuous, hence f(x) is continuous x ∈ = R – {0}
Let’s check the continuity at x = 0,
As, we know range of sin function is [-1,1]. So, -1 ≤ 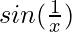 ≤ 1 which is a finite number.
≤ 1 which is a finite number.
Limit = 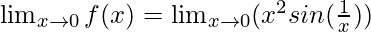
= (02 ×(finite number)) = 0
Function value at x = 0, f(0) = 0
As, 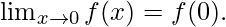
Hence, the function is continuous for any real number.
Question 25. Examine the continuity of f, where f is defined by
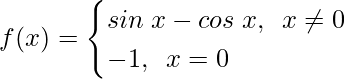
Solution:
Continuity at x = 0,
Left limit = 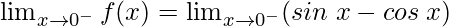
= (sin0 − cos0) = 0 − 1 = −1
Right limit = 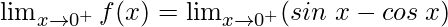
= (sin0 − cos0) = 0 − 1 = −1
Function value at x = 0, f(0) = sin 0 – cos 0 = 0 – 1 = -1
As, 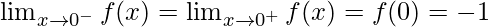
Hence, the function is continuous at x = 0.
Continuity at x = c (real number c≠0),
Left limit = 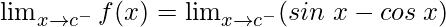
= (sinc − cosc)
Right limit = 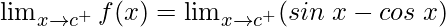
= (sinc − cosc)
Function value at x = c, f(c) = sin c – cos c
As, 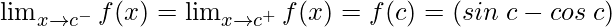
So concluding the results, we get
The function f(x) is continuous at any real number.
Find the values of k so that the function f is continuous at the indicated point in Exercises 26 to 29.
Question 26. 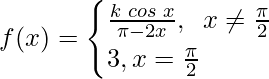 at x = π/2.
at x = π/2.
Solution:
Continuity at x = π/2
Let’s take x = 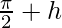
When x⇢π/2 then h⇢0
Substituting x = 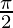 +h, we get
+h, we get
cos(A + B) = cos A cos B – sin A sin B
Limit = 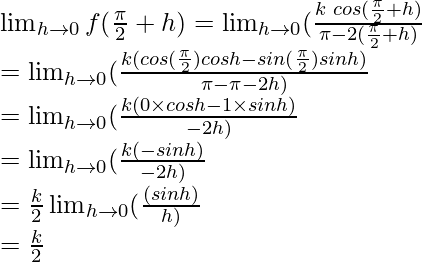
Function value at x = 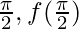 = 3
= 3
As, 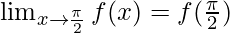 should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
k/2 = 3
k = 6
Question 27. 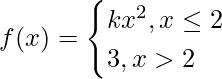 at x = 2
at x = 2
Solution:
Continuity at x = 2
Left limit = 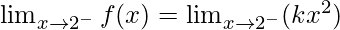
= k(2)2 = 4k
Right limit = 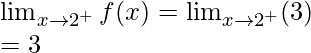
Function value at x = 2, f(2) = k(2)2 = 4k
As, 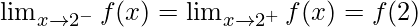 should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
4k = 3
k = 3/4
Question 28. 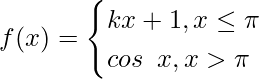 at x = π
at x = π
Solution:
Continuity at x = π
Left limit = 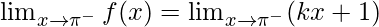
= k(π) + 1
Right limit = 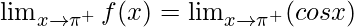
= cos(π) = -1
Function value at x = π, f(π) = k(π) + 1
As, 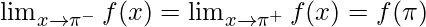 should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
kπ + 1 = -1
k = -2/π
Question 29. 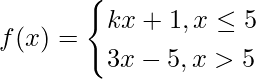 at x = 5
at x = 5
Solution:
Continuity at x = 5
Left limit = 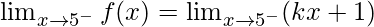
= k(5) + 1 = 5k + 1
Right limit = 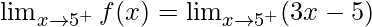
= 3(5) – 5 = 10
Function value at x = 5, f(5) = k(5) + 1 = 5k + 1
As, 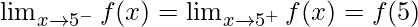 should satisfy, for f(x) being continuous
should satisfy, for f(x) being continuous
5k + 1 = 10
k = 9/5
Question 30. Find the values of a and b such that the function defined by
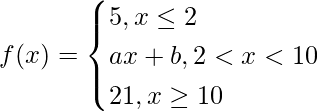
is a continuous function
Solution:
Continuity at x = 2
Left limit = 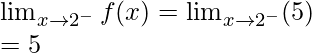
Right limit = 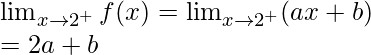
Function value at x = 2, f(2) = 5
As, 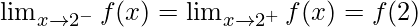 should satisfy, for f(x) being continuous at x = 2
should satisfy, for f(x) being continuous at x = 2
2a + b = 5 ……………………(1)
Continuity at x = 10
Left limit = 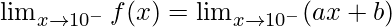
= 10a + b
Right limit = 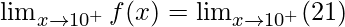
= 21
Function value at x = 10, f(10) = 21
As, 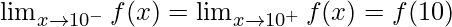 should satisfy, for f(x) being continuous at x = 10
should satisfy, for f(x) being continuous at x = 10
10a + b = 21 ……………………(2)
Solving the eq(1) and eq(2), we get
a = 2
b = 1
Question 31. Show that the function defined by f(x) = cos (x2) is a continuous function
Solution:
Let’s take
g(x) = cos x
h(x) = x2
g(h(x)) = cos (x2)
To prove g(h(x)) continuous, g(x) and h(x) should be continuous.
Continuity of g(x) = cos x
Let’s check the continuity at x = c
x = c + h
g(c + h) = cos (c + h)
When x⇢c then h⇢0
cos(A + B) = cos A cos B – sin A sin B
Limit = 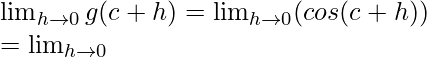 (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
= cosc cos0 − sinc sin0 = cosc
Function value at x = c, g(c) = cos c
As, 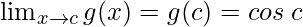
The function g(x) is continuous at any real number.
Continuity of h(x) = x2
Let’s check the continuity at x = c
Limit = 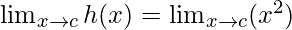
= c2
Function value at x = c, h(c) = c2
As, 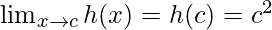
The function h(x) is continuous at any real number.
As, g(x) and h(x) is continuous then g(h(x)) = cos(x2) is also continuous.
Question 32. Show that the function defined by f(x) = | cos x | is a continuous function.
Solution:
Let’s take
g(x) = |x|
m(x) = cos x
g(m(x)) = |cos x|
To prove g(m(x)) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x – 0|, |x| = x when x ≥ 0 and |x| = -x when x < 0
Let’s check the continuity at x = c
When c < 0
Limit = 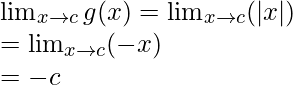
Function value at x = c, g(c) = |c| = -c
As, 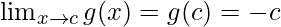
When c ≥ 0
Limit = 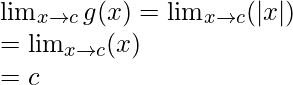
Function value at x = c, g(c) = |c| = c
As, 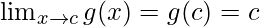
The function g(x) is continuous at any real number.
Continuity of m(x) = cos x
Let’s check the continuity at x = c
x = c + h
m(c + h) = cos (c + h)
When x⇢c then h⇢0
cos(A + B) = cos A cos B – sin A sin B
Limit = 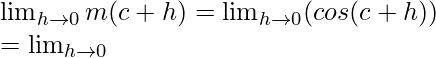 (cosc cosh − sinc sinh)
(cosc cosh − sinc sinh)
= cosc cos0 − sinc sin0 = cosc
Function value at x = c, m(c) = cos c
As, 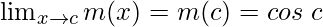
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then g(m(x)) = |cos x| is also continuous.
Question 33. Examine that sin | x | is a continuous function.
Solution:
Let’s take
g(x) = |x|
m(x) = sin x
m(g(x)) = sin |x|
To prove m(g(x)) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x-0|, |x|=x when x≥0 and |x|=-x when x<0
Let’s check the continuity at x = c
When c < 0
Limit = 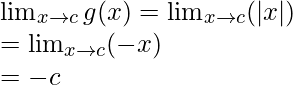
Function value at x = c, g(c) = |c| = -c
As, 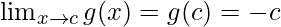
When c ≥ 0
Limit = 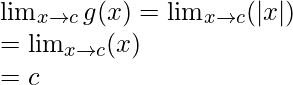
Function value at x = c, g(c) = |c| = c
As, 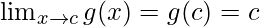
The function g(x) is continuous at any real number.
Continuity of m(x) = sin x
Let’s check the continuity at x = c
x = c + h
m(c + h) = sin (c + h)
When x⇢c then h⇢0
sin(A + B) = sin A cos B + cos A sin B
Limit = 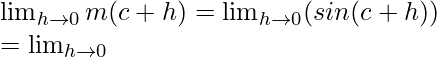 (sinc cosh + cosc sinh)
(sinc cosh + cosc sinh)
= sinc cos0 + cos csin0 = sinc
Function value at x = c, m(c) = sin c
As, 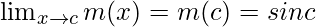
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then m(g(x)) = sin |x| is also continuous.
Question 34. Find all the points of discontinuity of f defined by f(x) = | x | – | x + 1 |
Solution:
Let’s take
g(x) = |x|
m(x) = |x + 1|
g(x) – m(x) = | x | – | x + 1 |
To prove g(x) – m(x) continuous, g(x) and m(x) should be continuous.
Continuity of g(x) = |x|
As, we know that modulus function works differently.
In |x – 0|, |x| = x when x≥0 and |x| = -x when x < 0
Let’s check the continuity at x = c
When c < 0
Limit = 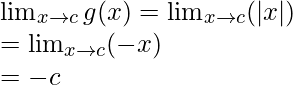
Function value at x = c, g(c) = |c| = -c
As, 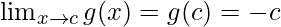
When c ≥ 0
Limit = 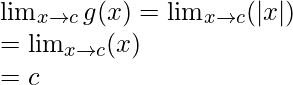
Function value at x = c, g(c) = |c| = c
As, 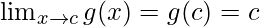
The function g(x) is continuous at any real number.
Continuity of m(x) = |x + 1|
As, we know that modulus function works differently.
In |x + 1|, |x + 1| = x + 1 when x ≥ -1 and |x + 1| = -(x + 1) when x < -1
Let’s check the continuity at x = c
When c < -1
Limit = 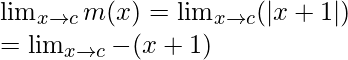
= -(c + 1)
Function value at x = c, m(c) = |c + 1| = -(c + 1)
As, 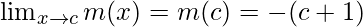
When c ≥ -1
Limit = 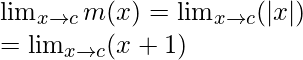
= c + 1
Function value at x = c, m(c) = |c| = c + 1
As, 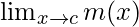 = m(c) = c + 1
= m(c) = c + 1
The function m(x) is continuous at any real number.
As, g(x) and m(x) is continuous then g(x) – m(x) = |x| – |x + 1| is also continuous.
Share your thoughts in the comments
Please Login to comment...