Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.5 | Set 1

Question 1. Sides of triangles are given below. Determine which of them are right triangles? In the case of a right triangle, write the length of its hypotenuse.

(i) 7 cm, 24 cm, 25 cm

(ii) 3 cm, 8 cm, 6 cm

(iii) 50 cm, 80 cm, 100 cm

(iv) 13 cm, 12 cm, 5 cm

Solution:

(i) Given: 7cm, 24cm, 25cm
(25)²= 25 * 25 = 625
∴They are sides of a right ∆ and hypotenuse = 625
(ii) Given: 3cm, 8cm, 6cm
(8)² = 8 * 8 = 64
They are not side of right triangle.
(iii) Given: 50cm, 80cm, 100cm
(100)²= 100 * 100 = 10000
(50)²+ (80)²= 2500 + 6400
Therefore, this is not right triangle.
(iv) Given: 13cm, 12cm, 5cm
(13)²= 13 * 13 = 169
(12)²+ (5)²= 169
Therefore, this is the sides of right triangle and hypotenuse = 169

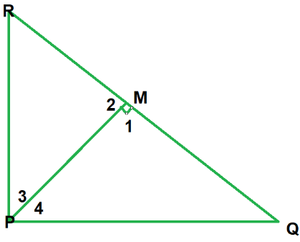
Question 2. PQR is a triangle right-angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM × MR.

Solution:

Given: A right ∆PQR right-angled at P and PM⊥QR
To show: PM² = QM * MR
PM * PM = QM * MR
In ∆PMQ and ∆PMR
∠1 =∠2 -(each 90°)
∠1 +∠2 +∠3 = 180°
90° + ∠4 + ∠5 = 180°
∠4 +∠5 = 180° – 90°
∠3 + ∠4 = 180° – 90°
∠4 +∠5 = ∠3 +∠4
∴∠5 =∠3
∴∆PMQ ~ ∆RMP
$\frac{PM}{RM} = \frac{MQ}{MP} = \frac{QP}{PR}$
$\frac{PM}{RM} = \frac{MQ}{MP}$
MP²= MQ.PM

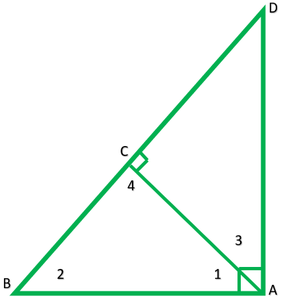
Question 3. In Fig., ABD is a triangle right angled at A and AC ⊥ BD. Show that

(i) AB² = BC × BD

(ii) AC² = BC × DC

(iii) AD² = BD × CD

Solution:

Given: A right ∆ABD, right angled at A and AC⊥ BD
To show:
(i)AB² = BC × BD
(ii) AC² = BC × DC
(iii) AD² = BD × CD
(i) AB²= BC × BD
AB * AB = BC.BD
In ∆ ABC and ∆ABD
∠B =∠B -(common)
∠BCA = ∠A -(each 90°)
∴ ∆ABC~∆DBA
$\frac{AB}{DB} = \frac{BC}{BA} = \frac{CA}{AD}$
AB²= BC * DC
(ii) AC²= BC * DC
AC * AC = BC * DC
In ∆ABC and ∆ACD
∠ACB = ∠ACD -(each 90°)
In ∆ ACB
∠1 + ∠2 + ∠3 = 180°
∠1 + ∠2 + 90° = 180°
∠1 + ∠2 = 90° -(1)
∠1 + ∠3 = 90° -(2)
∠1 + ∠2 =∠1 + ∠3
∴ ∠2 = ∠3
∴ ∆ABC~∆DAC
$\frac{AB}{DA} = \frac{BC}{AC} = \frac{CA}{CD}$
AC²= BC * CD
(iii) AD² = BD × CD
In ∆ABD and ∆ACD
∠A =∠ACD -(each 90)
∠D =∠D -(common)
∴ ∆ABD~∆CAD -(AA similarity)
$\frac{AB}{CA} = \frac{BD}{AD} = \frac{DA}{DC}$
AD²= BD * CD

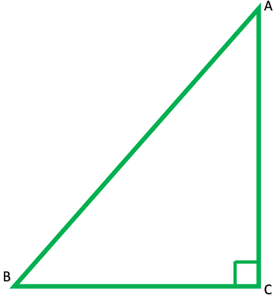
Question 4. ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².

Solution:

Given: ∆ABC right angled at B
To prove: AB²= 2AC²
According to Pythagoras theorem,
(AB)²= (AC)²+ (BC)²
(AB)²= (AC)²+ (AC)² -(BC = AC)
AB²= 2AC²

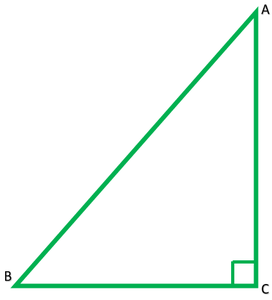
Question 5. ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ABC is a right triangle.

Solution:

Given: ∆ABC is an isosceles triangle in which
AC = BC
AB²= 2AC²
To prove: ABCD is right ∆
AB²= 2AC²
AB²= AC² + AC²
∴ By the, converse of Pythagoras theorem ∆ACB is a right ∆ at C.

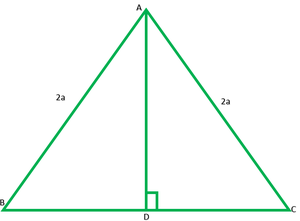
Question 6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.

Solution:

Let ABC is an equilateral triangle of each 2a units
Construction: Draw AD ⊥ BC
In right ∆ ADB
(AB)²= (AD)²+ (BD)²
(2a)²= (AD)²+ (a)²
(4a)²= (AD)²+ a²
4a²– a²= (AD)²
3a²= (AB)²
√3 a²= AD ∴ Each of its altitude= √3 a unit
√3 a = AD

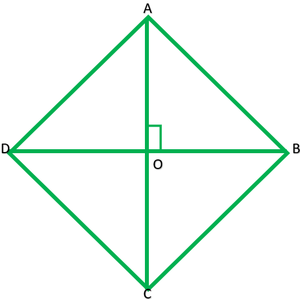
Question 7. Prove that the sum of the squares of the sides of the rhombus is equal to the sum of the squares of its diagonals.

Solution:

Given: ABCD is a rhombus
To prove: AB²+ BC²+ CD²+ DA²
Proof: ABCD is rhombus and let diagonals AC and BD bisect each other at O.
∴ ∠AOB =∠BOC =∠COD =∠DOA = 90°
In ∆AOB
AB² = AC²+ BO²
AB²= (1/2AC²) + (1/2BD²)
AB²= 1/4(AC²+ BD²)
4AB²= AC²+ BD² -(1)
Similarly, in ∆BOC
4BC²= AC²+ BD² -(2)
4CD²= AC²+ BD² -(3)
4AD²= AC²+ BD² -(4)
Adding 1, 2, 3, and 4
4AB²+ 4BC²+ 4CD²+ 4DA²= 4(AC²+ BD²)
4(AB²+ BC²+ CD²+ DA²) = 4(AC²+ BD²)
∴ AB²+ BC²+ CD²+ DA²= AC²+ BD²

Question 8. In Fig. 6.54, O is a point in the interior of a triangle diagonals.

(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii) AF² + BD² + CE² = AE² + CD² + BF²

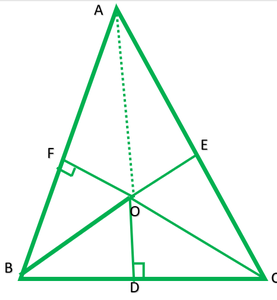
Solution:

(i) In right ∆AFO, by Pythagoras theorem
OA²= AP²+ OF² -(1)
In right ∆ODB, by Pythagoras theorem
OB²= BD²+ OD² -(2)
In right ∆OEC, by Pythagoras theorem
OC²= CE²+ OE² -(3)
Adding 1, 2, and 3
OA²+ OB²+ OC²= AF²+ BD²+ CF²+ OD²+ OE²
OA² + OB²+ OC²– OE²– OD²– OE² = AF²+ BD²+ CE²
(ii) AF²+ BD²+ CE²= AE²+ CD²+ BF²
OB²= BD²+ OD² -(1)
OC²= DC²+ OD² -(2)
Subtracting (1) from (2) we get,
OB²– OC²= BD²+ OD²– (DC²+ OD²)
= BD²+ OD²– DC²– OD²
= BD²– DC² -(3)
Similarly,
OC²– AD²= CE²– EA² -(4)
AO²= BO²= AF²– FB² -(5)
Adding 3, 4, and 5, we get,
OB²– OC²+ OC²– AO²+ AO²– BO²= BD²– DC²+ CE²– EA²+ AF²– FB²
0 + DC²+ EA²+ FB²= BD²+ CD²+ AF²

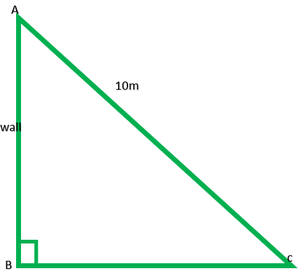
Question 9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.

Solution:

AB is wall = 8m
AC is ladder = 10m
BC = ?
In right ∆ABC, by Pythagoras theorem
(AC)²= (AB)²+ (BC)²
(10)²= (8)²+ (BC)²
100 = 64 + (BC)²
100 – 64 = (BC)²
36 = (BC)²
√36 = BC
√(6 * 6) = BC
6 = BC
Hence, the foot of the ladder is at a distance of 6 m from the base of the wall.

Question 10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Solution:

In fig.
AB is pole = 18m
AC is wire = 24m
BC = ?
In right ∆ABC, by Pythagoras theorem
(AC)²= (AB)²+ (BC)²
(24)²= (18)²+ (BC)²
576 = 324 + (BC)²
576 – 324 = (BC)²
252 = (BC)²
√252 = BC
√(2 * 2 * 3 * 3 * 7) = BC
2 * 3√7 = BC
6√7 = BC
∴ Hence, the stake may be placed at distance of 6√7 from the base of the pole.