Class 10 NCERT Solutions- Chapter 13 Surface Areas And Volumes – Exercise 13.4
Last Updated :
04 Mar, 2021
Question 1. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Given values:
Height of frustum (h) = 14 cm
Radius of larger circle end (R) = 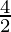 = 2 cm
= 2 cm
Radius of smaller circle end (r)=  = 1 cm
= 1 cm

Capacity of frustum-shaped glass = Volume of Frustum
= 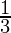 πh (r2 + R2 + rR)
πh (r2 + R2 + rR)
= 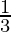 × π × 14 ((1 × 1) + (2 × 2) × (2 × 1))
× π × 14 ((1 × 1) + (2 × 2) × (2 × 1))
= 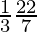 × 14 × 7 (taking π=
× 14 × 7 (taking π=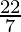 )
)
= 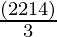
= 102.67 cm3
Hence, the capacity of frustum-shaped glass = 102.67 cm3
Question 2. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
Slant height of frustum (l) = 4 cm
Let radius of smaller circle end = r
Let radius of larger circle end = R

Circumference of circle = 2π × (radius of circle)
Circumference of larger circle = 2πR
18 cm2 = 2πR
R = 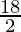
R = 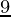 cm
cm
Circumference of smaller circle = 2πr
6 cm2 = 2πr
r = 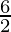
r = 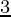 cm
cm
Now, as curve surface area of frustum = π (r+R) l
= π × (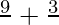 ) × 4
) × 4
= 12 × 4 (Taking π common and canceling it)
= 48cm2
Hence, the curved surface area of the frustum = 48cm2
Question 3. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see Fig.). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Solution:
Given values:
Slant height of frustum (l)= 15 cm
Let radius of smaller circle end (r) = 4 cm
Let radius of larger circle end (R) = 10 cm

Area of material used for making it = Curve surface area + area of upper base
= (π(r+R)l) + (πr2)
= π ((r+R)l + r2) (Taking π common)
= π ((4+10) × 15 + (4 × 4))
= 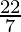 × (226) (Taking π =
× (226) (Taking π = 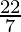 )
)
= 710.286 cm2
Hence, the area of material used for making it = 710.286 cm2
Question 4. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2. (Take π = 3.14)
Solution:
Given values:
Height of frustum (h)= 16 cm
Let radius of smaller circle end (r) = 8 cm
Let radius of larger circle end (R) = 20 cm

The amount of milk to fill the container = Volume of frustum
= 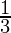 πh (r2 + R2 + rR)
πh (r2 + R2 + rR)
= 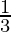 × 3.14 × 16 (8×8 + 20×20 + 8×20) (Taking π=3.14)
× 3.14 × 16 (8×8 + 20×20 + 8×20) (Taking π=3.14)
= 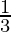 × 3.14 × 16 × (624)
× 3.14 × 16 × (624)
= 10449.92 cm3
Cost of 1 litre milk = ₹ 20
And as, 1 m3 = 1000 cm3 = 1 litre
10449.92 cm3 = (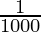 ) ×10449.92 litres
) ×10449.92 litres
cost of 10449.92 cm3 = (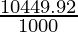 ) × 20
) × 20
= ₹ 208.998
Now, metal sheet used to make the container = Curve surface area + area of lower base
= (π(r+R)l) + (πr2)
= π ((r+R)l + r2) (Taking π common)
= π ((20+8) × (√(162+(20-8)2)) + (8 × 8)) (Slant height (l) = √(h2+(R-r)2))
= 3.14 × (28 × √400 + 64) (Taking π = 3.14)
= 3.14 × (624)
= 1959.36 cm2
Hence, the metal sheet used to make the container = 1959.36 cm2
As, cost of 100 cm2= ₹ 8
1959.36 cm2 = (8/100) × 1959.36
= ₹156.748
Hence, the cost of the milk which can completely fill the container = ₹ 208.998
and, the cost of metal sheet used to make the container = ₹156.748
Question 5. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire.
Solution:
As the angle is cut into two equal parts, the height gets half too.
Let radius of smaller circle end = r
Let radius of larger circle end = R

In ∆PFR and ∆PEB
tan ∝ = 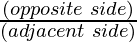
tan 30° = 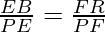
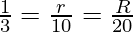
R = 
r = 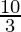
and as height of frustum = 10 cm
So according to the question,
Frustum is converted to cylindrical wire having diameter 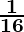 cm
cm
Volume of Frustum = Volume of Cylinder
Volume of Frustum = 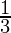 πh (r2 + R2 + rR)
πh (r2 + R2 + rR)
= 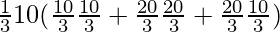
= 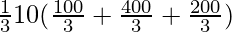
= 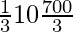
= 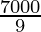 cm3 ………………………..(1)
cm3 ………………………..(1)
Volume of Cylinder = 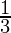 π(radius)2H
π(radius)2H
= 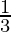 π(
π(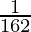 )2H …………………(2)
)2H …………………(2)
As (1) = (2) , then
7000π / 9 = 1/3 π(1/(16×2))2H
H = 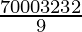 (cancel π from both side)
(cancel π from both side)
H = 796444.443 cm
H = 7964.44 m
Hence, the length of the wire = 7964.44 m
Share your thoughts in the comments
Please Login to comment...