Carry Look-Ahead Adder
Last Updated :
23 Feb, 2023
The adder produce carry propagation delay while performing other arithmetic operations like multiplication and divisions as it uses several additions or subtraction steps. This is a major problem for the adder and hence improving the speed of addition will improve the speed of all other arithmetic operations. Hence reducing the carry propagation delay of adders is of great importance. There are different logic design approaches that have been employed to overcome the carry propagation problem. One widely used approach is to employ a carry look-ahead which solves this problem by calculating the carry signals in advance, based on the input signals. This type of adder circuit is called a carry look-ahead adder.
Here a carry signal will be generated in two cases:
- Input bits A and B are 1
- When one of the two bits is 1 and the carry-in is 1.
In ripple carry adders, for each adder block, the two bits that are to be added are available instantly. However, each adder block waits for the carry to arrive from its previous block. So, it is not possible to generate the sum and carry of any block until the input carry is known. The 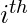 block waits for the
block waits for the 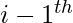 block to produce its carry. So there will be a considerable time delay which is carry propagation delay.
block to produce its carry. So there will be a considerable time delay which is carry propagation delay.

Consider the above 4-bit ripple carry adder. The sum 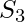 is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input
is produced by the corresponding full adder as soon as the input signals are applied to it. But the carry input 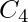 is not available on its final steady-state value until carry
is not available on its final steady-state value until carry 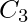 is available at its steady-state value. Similarly
is available at its steady-state value. Similarly 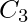 depends on
depends on 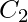 and
and 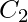 on
on 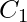 . Therefore, though the carry must propagate to all the stages in order that output
. Therefore, though the carry must propagate to all the stages in order that output 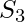 and carry
and carry 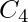 settle their final steady-state value.
settle their final steady-state value.
The propagation time is equal to the propagation delay of each adder block, multiplied by the number of adder blocks in the circuit. For example, if each full adder stage has a propagation delay of 20 nanoseconds, then 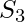 will reach its final correct value after 60 (20 × 3) nanoseconds. The situation gets worse, if we extend the number of stages for adding more number of bits.
will reach its final correct value after 60 (20 × 3) nanoseconds. The situation gets worse, if we extend the number of stages for adding more number of bits.
Carry Look-ahead Adder :
A carry look-ahead adder reduces the propagation delay by introducing more complex hardware. In this design, the ripple carry design is suitably transformed such that the carry logic over fixed groups of bits of the adder is reduced to two-level logic. Let us discuss the design in detail.
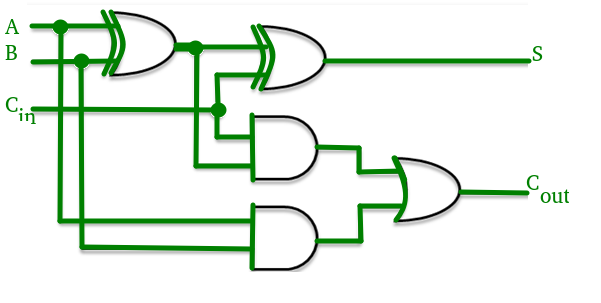

Consider the full adder circuit shown above with corresponding truth table. We define two variables as ‘carry generate’ 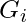 and ‘carry propagate’
and ‘carry propagate’ 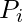 then,
then,
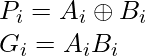
The sum output and carry output can be expressed in terms of carry generate 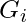 and carry propagate
and carry propagate 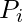 as
as
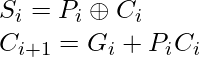
where 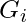 produces the carry when both
produces the carry when both 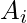 ,
, 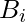 are 1 regardless of the input carry.
are 1 regardless of the input carry. 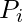 is associated with the propagation of carry from
is associated with the propagation of carry from 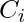 to
to 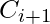 .
.
The carry output Boolean function of each stage in a 4 stage carry look-ahead adder can be expressed as
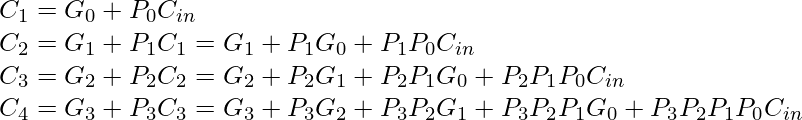
From the above Boolean equations we can observe that 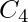 does not have to wait for
does not have to wait for 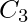 and
and 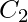 to propagate but actually
to propagate but actually 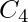 is propagated at the same time as
is propagated at the same time as 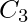 and
and 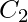 . Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate.
. Since the Boolean expression for each carry output is the sum of products so these can be implemented with one level of AND gates followed by an OR gate.
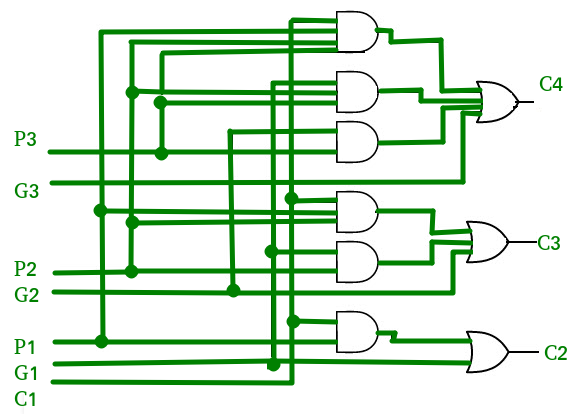
The implementation of three Boolean functions for each carry output (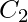 ,
, 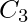 and
and 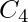 ) for a carry look-ahead carry generator shown in below figure.
) for a carry look-ahead carry generator shown in below figure.
Time Complexity Analysis :
We could think of a carry look-ahead adder as made up of two “parts”
- The part that computes the carry for each bit.
- The part that adds the input bits and the carry for each bit position.
The 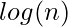 complexity arises from the part that generates the carry, not the circuit that adds the bits.
complexity arises from the part that generates the carry, not the circuit that adds the bits.
Now, for the generation of the 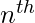 carry bit, we need to perform a AND between (n+1) inputs. The complexity of the adder comes down to how we perform this AND operation. If we have AND gates, each with a fan-in (number of inputs accepted) of k, then we can find the AND of all the bits in
carry bit, we need to perform a AND between (n+1) inputs. The complexity of the adder comes down to how we perform this AND operation. If we have AND gates, each with a fan-in (number of inputs accepted) of k, then we can find the AND of all the bits in 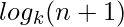 time. This is represented in asymptotic notation as
time. This is represented in asymptotic notation as 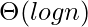 .
.
Advantages and Disadvantages of Carry Look-Ahead Adder :
Advantages –
- The propagation delay is reduced.
- It provides the fastest addition logic.
Disadvantages –
- The Carry Look-ahead adder circuit gets complicated as the number of variables increase.
- The circuit is costlier as it involves more number of hardware.
NOTE :
For n-bit carry lookahead adder to evaluate all the carry bits it requires [n(n + 1)]/2 AND gates and n OR gates.
GATE CS Corner Questions
Practicing the following questions will help you test your knowledge. All questions have been asked in GATE in previous years or in GATE Mock Tests. It is highly recommended that you practice them.
- GATE CS 2016 (Set-1), Question 43
- GATE CS 2004, Question 90
- GATE CS 2007, Question 85
- GATE CS 2006, Question 85
- GATE CS 1997, Question 15
References –
iitkgp.virtual-labs
Carry-lookahead adder – Wikipedia
Share your thoughts in the comments
Please Login to comment...