What is Correlation?
A statistical tool that helps in the study of the relationship between two variables is known as Correlation. It also helps in understanding the economic behaviour of the variables. However, correlation does not tell anything about the cause-and-effect relationship between the two variables. Correlation can be measured through three different methods; viz., Scatter Diagram, Karl Pearson’s Coefficient of Correlation, and Spearman’s Rank Correlation Coefficient.
According to L.R. Connor, “If two or more quantities vary in sympathy so that movements in one tend to be accompanied by corresponding movements in others, then they are said to be correlated.”
What is Karl Pearson’s Coefficient of Correlation?
The first person to give a mathematical formula for the measurement of the degree of relationship between two variables in 1890 was Karl Pearson. Karl Pearson’s Coefficient of Correlation is also known as Product Moment Correlation or Simple Correlation Coefficient. This method of measuring coefficient of correlation is the most popular and is widely used. It is denoted by ‘r’, where r is a pure number which means that r has no unit.
According to Karl Pearson, “Coefficient of Correlation is calculated by dividing the sum of products of deviations from their respective means by their number of pairs and their standard deviations.”
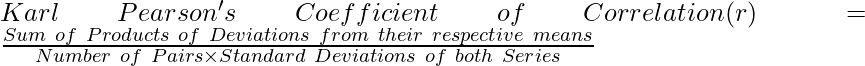
Or
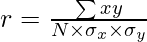
Where,
N = Number of Pair of Observations
x = Deviation of X series from Mean 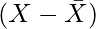
y = Deviation of Y series from Mean 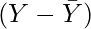
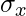 = Standard Deviation of X series
= Standard Deviation of X series 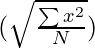
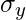 = Standard Deviation of Y series
= Standard Deviation of Y series 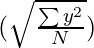
r = Coefficient of Correlation
Karl Pearson’s Coefficient of Correlation method can be used only when there is availability of quantitative measurements of different items of a series. However, there are various cases in which the direct measurement of the phenomenon under study is not possible. For example, different qualitative measures such as ability, kindness, honesty, beauty, etc., cannot be measured in quantitative terms. To study the correlation between two qualitative measures, one should use Spearman’s Rank Correlation.
Karl Pearson’s Coefficient of Correlation and Covariance
Karl Pearson’s method of determining coefficient of correlation is based on the covariance of the given variables. Covariance is a statistical representation of the degree to which the two given variables vary together. Basically, Covariance is a number reflecting the degree to which the two variables vary together. The symbol of Covariance of two variables (say X and Y) is denoted by COV(X, Y).
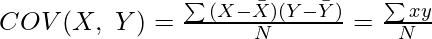
The formula for calculating Karl Pearson’s Coefficient of Correlation can be transformed into another easy formula as:
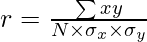
Or, 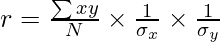
Or, 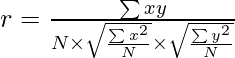
Or, 
Note: This method of determining Coefficient of Correlation should be applied only when the deviations of items are taken from actual means and not from assumed means.
Example 1:
Determine the Coefficient of Correlation between X and Y.

The summation of the product of deviations of Series X and Y from their respective means is 200.
Solution:
The figures given are:
N = 30, σx = 4, σy = 3, and ∑xy = 200
Coefficient of Correlation = 0.5
It means that there is a positive correlation between X and Y.
Example 2:
If the Covariance between two variables X and Y is 9.4 and the variance of Series X and Y are 10.6 and 12.5, respectively, then calculate the coefficient of correlation.
Solution:
Covariance between X and Y = 
Variance of X = σx2 = 10.6
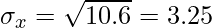
Variance of Y = σy2 = 12.5
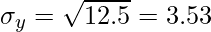
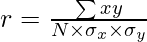
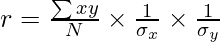
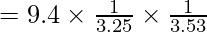
r = 9.4 x 0.307 x 0.282 = 0.816
Coefficient of Correlation = 0.816
It means that there is quite a high degree of positive correlation between X and Y.
Features of Karl Pearson’s Coefficient of Correlation
The main features of Karl Pearson’s Coefficient of Correlation are as follows:
1. Knowledge of Direction of Correlation: This method of measuring coefficient of correlation gives us knowledge about the direction of the relationship between two variables. In other words, it tells us whether the relationship between two variables is positive or negative.
2. Size of Correlation: Karl Pearson’s Coefficient of Correlation indicates the size of the relationship between two variables. Besides, Correlation Coefficient ranges between -1 and +1.
3. Indicates Magnitude and Direction: This method not only specifies the magnitude of the correlation between two variables but also specifies its direction. It means that, if two variables are directly related, then the correlation coefficient between the variables will be a positive value. However, if two variables are inversely related, then the correlation coefficient between the variables will be a negative value.
4. Ideal Measure: As this method is based on the most essential statistical measure, such as standard deviation and mean, it is an ideal/appropriate measure.
Note: The value of the Correlation Coefficient should always lie between -1 and +1.
- When r = +1, it means that there is perfect positive correlation.
- When r = -1, it means that there is perfect negative correlation.
- When r = 0, it means that there is no or zero correlation.
Assumptions of Coefficient of Correlation
The assumptions on which Karl Pearson’s Coefficient of Correlation is based are as follows:
1. Linear Relationship: The first assumption in this method is that there is a linear relationship between the given two variables. It means that if the paired observations of the variables (say X and Y) are plotted on a scatter diagram, then it will always form a straight line.
2. Casual Relationship: Another assumption is that there is no cause-and-effect relationship between the given two variables. However, the cause-and-effect relationship exists between the forces affecting these variables. Besides, if there is no such type of relationship between the variables, then the correlation is meaningless.
3. Normal Distribution: It is also assumed that, if there are a large number of independent causes of some nature producing normal distribution, then the two given variables are affected by them. For example, Variables like demand, supply, height, weight, etc., are affected by multiple forces.
4. Error of Measurement: If the error of measurement is reduced to the minimum, then the coefficient of correlation is more reliable.
Properties of Coefficient of Correlation
1. Coefficient of Correlation is Independent of change of origin and scale of measurements: Coefficient of Correlation is not affected by the change of origin and scale of measurement.
2. Coefficient of Correlation lies between -1 and +1: The property of r also serves as a useful check on the correctness of the calculations. If the value of r lies outside the range, then it would mean that there is some error in the calculations.
3. Zero Correlation: If two variables (say X and Y) are independent of each other, in that case, the coefficient of correlation between them will be zero.
4. Measure of Linear Relationship: The coefficient of correlation is a measure that helps in determining the linear relationship between two variables. If both the variables (say X and Y) increase or decrease together, then r will be positive. However, if one variable increases when the other variable decreases or vice-versa, then r will be negative.
Merits of Karl Pearson’s Coefficient of Correlation
Various advantages of Karl Pearson’s Coefficient of Correlation are as follows:
1. Popular Method: Karl Pearson’s Coefficient of Correlation is the most popular and widely used mathematical method to study the correlation between two variables.
2. Degree and Direction of Correlation: The value of correlation coefficient not only summarises the degree of correlation but also its direction.
Demerits of Karl Pearson’s Coefficient of Correlation
Various disadvantages of Karl Pearson’s Coefficient of Correlation are as follows:
1. Affected by Extreme Values: If the values of the two variables are extreme, then it would have a great impact on the value of correlation coefficient.
2. Assumption of Linear Relationship: While determining correlation coefficient, it is always assumed that there is a linear relationship without thinking whether the assumption is correct or not.
3. Time-Consuming Method: In comparison to other methods of determining correlation coefficients, this method takes more time.
4. Possibility of Wrong Interpretation: While interpreting the value of coefficient of correlation using this method, one has to be very careful. It is because the chances of misinterpreting the coefficient are more.
Share your thoughts in the comments
Please Login to comment...