Bitonic Sort
Last Updated :
28 Dec, 2023
Background
Bitonic Sort is a classic parallel algorithm for sorting.
- The number of comparisons done by Bitonic sort is more than popular sorting algorithms like Merge Sort [ does O(log N) comparisons], but Bitonic sort is better for parallel implementation because we always compare elements in a predefined sequence and the sequence of comparison doesn’t depend on data. Therefore it is suitable for implementation in hardware and parallel processor array.
- Bitonic Sort can only be done if the number of elements to sort is 2^n. The procedure of bitonic sequence fails if the number of elements is not in the aforementioned quantity precisely.
To understand Bitonic Sort, we must first understand what is Bitonic Sequence and how to make a given sequence Bitonic.
Bitonic Sequence
A sequence is called Bitonic if it is first increasing, then decreasing. In other words, an array arr[0..n-i] is Bitonic if there exists an index I, where 0<=i<=n-1 such that
x0 <= x1 …..<= xi
and
xi >= xi+1….. >= xn-1
- A sequence, sorted in increasing order is considered Bitonic with the decreasing part as empty. Similarly, decreasing order sequence is considered Bitonic with the increasing part as empty.
- A rotation of the Bitonic Sequence is also bitonic.
How to form a Bitonic Sequence from a random input?
We start by forming 4-element bitonic sequences the from consecutive 2-element sequences. Consider 4-element in sequence x0, x1, x2, x3. We sort x0 and x1 in ascending order and x2 and x3 in descending order. We then concatenate the two pairs to form a 4 element bitonic sequence.
Next, we take two 4-element bitonic sequences, sorting one in ascending order, the other in descending order (using the Bitonic Sort which we will discuss below), and so on, until we obtain the bitonic sequence.
Example:
Convert the following sequence to a bitonic sequence: 3, 7, 4, 8, 6, 2, 1, 5
Step 1: Consider each 2-consecutive element as a bitonic sequence and apply bitonic sort on each 2- pair element. In the next step, take 4-element bitonic sequences and so on.

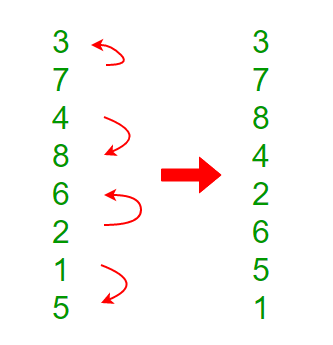
Note: x0 and x1 are sorted in ascending order and x2 and x3 in descending order and so on
Step 2: Two 4 element bitonic sequences: A(3,7,8,4) and B(2,6,5,1) with comparator length as 2
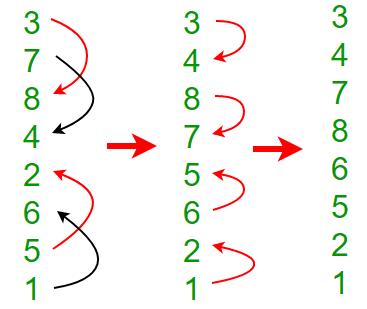
After this step, we’ll get a Bitonic sequence of length 8.
3, 4, 7, 8, 6, 5, 2, 1
Bitonic Sorting
Bitonic Sort Algorithm:
- Bitonic sequence is created.
- Comparison between the corresponding element of the bitonic sequence.
- Swapping the second element of the sequence.
- Swapping the adjacent element.
It mainly involves two steps.
- Form a bitonic sequence (discussed above in detail). After this step we reach the fourth stage in the below diagram, i.e., the array becomes {3, 4, 7, 8, 6, 5, 2, 1}
- Creating one sorted sequence from a bitonic sequence: After the r first state ep, the first half is sorted in increasing order and the second half in decreasing order.
We compare the first element of the first half with the first element of the second half, then the second element of the first half with the second element of the second, and so on. We exchange elements if an element of the first half is larger than second half.
After her above compare and exchange steps, we get two bitonic sequences in the array. See the fifth stage below the diagram. In the fifth stage, we have {3, 4, 2, 1, 6, 5, 7, 8}. If we take a closer look at the elements, we can notice that there are two bitonic sequences of length n/2 such that all elements in the first bitonic sequence {3, 4, 2, 1} are smaller than all elements of the second bitonic sequence {6, 5, 7, 8}.
We repeat the same process within two bitonic sequences and we get four bitonic sequences of length n/4 such that all elements of the leftmost bitonic sequence are smaller and all elements of the rightmost. See sixth stage in below diagram, arrays is {2, 1, 3, 4, 6, 5, 7, 8}.
If we repeat this process one more time we get 8 bitonic sequences of size n/8 which is 1. Since all these bitonic sequences are sorted and every bitonic sequence has one element, we get the sorted array.

Below are implementations of Bitonic Sort.
C++
#include<bits/stdc++.h>
using namespace std;
void compAndSwap(int a[], int i, int j, int dir)
{
if (dir==(a[i]>a[j]))
swap(a[i],a[j]);
}
void bitonicMerge(int a[], int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
for (int i=low; i<low+k; i++)
compAndSwap(a, i, i+k, dir);
bitonicMerge(a, low, k, dir);
bitonicMerge(a, low+k, k, dir);
}
}
void bitonicSort(int a[],int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
bitonicSort(a, low, k, 1);
bitonicSort(a, low+k, k, 0);
bitonicMerge(a,low, cnt, dir);
}
}
void sort(int a[], int N, int up)
{
bitonicSort(a,0, N, up);
}
int main()
{
int a[]= {3, 7, 4, 8, 6, 2, 1, 5};
int N = sizeof(a)/sizeof(a[0]);
int up = 1;
sort(a, N, up);
printf("Sorted array: \n");
for (int i=0; i<N; i++)
printf("%d ", a[i]);
return 0;
}
|
Java
public class BitonicSort
{
void compAndSwap(int a[], int i, int j, int dir)
{
if ( (a[i] > a[j] && dir == 1) ||
(a[i] < a[j] && dir == 0))
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
void bitonicMerge(int a[], int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
for (int i=low; i<low+k; i++)
compAndSwap(a,i, i+k, dir);
bitonicMerge(a,low, k, dir);
bitonicMerge(a,low+k, k, dir);
}
}
void bitonicSort(int a[], int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
bitonicSort(a, low, k, 1);
bitonicSort(a,low+k, k, 0);
bitonicMerge(a, low, cnt, dir);
}
}
void sort(int a[], int N, int up)
{
bitonicSort(a, 0, N, up);
}
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
public static void main(String args[])
{
int a[] = {3, 7, 4, 8, 6, 2, 1, 5};
int up = 1;
BitonicSort ob = new BitonicSort();
ob.sort(a, a.length,up);
System.out.println("\nSorted array");
printArray(a);
}
}
|
Python3
def compAndSwap(a, i, j, dire):
if (dire==1 and a[i] > a[j]) or (dire==0 and a[i] < a[j]):
a[i],a[j] = a[j],a[i]
def bitonicMerge(a, low, cnt, dire):
if cnt > 1:
k = cnt//2
for i in range(low , low+k):
compAndSwap(a, i, i+k, dire)
bitonicMerge(a, low, k, dire)
bitonicMerge(a, low+k, k, dire)
def bitonicSort(a, low, cnt,dire):
if cnt > 1:
k = cnt//2
bitonicSort(a, low, k, 1)
bitonicSort(a, low+k, k, 0)
bitonicMerge(a, low, cnt, dire)
def sort(a,N, up):
bitonicSort(a,0, N, up)
a = [3, 7, 4, 8, 6, 2, 1, 5]
n = len(a)
up = 1
sort(a, n, up)
print ("\n\nSorted array is")
for i in range(n):
print("%d" %a[i],end=" ")
|
C#
using System;
class GFG
{
static void Swap<T>(ref T lhs, ref T rhs)
{
T temp;
temp = lhs;
lhs = rhs;
rhs = temp;
}
public static void compAndSwap(int[] a, int i, int j, int dir)
{
int k;
if((a[i]>a[j]))
k=1;
else
k=0;
if (dir==k)
Swap(ref a[i],ref a[j]);
}
public static void bitonicMerge(int[] a, int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
for (int i=low; i<low+k; i++)
compAndSwap(a, i, i+k, dir);
bitonicMerge(a, low, k, dir);
bitonicMerge(a, low+k, k, dir);
}
}
public static void bitonicSort(int[] a,int low, int cnt, int dir)
{
if (cnt>1)
{
int k = cnt/2;
bitonicSort(a, low, k, 1);
bitonicSort(a, low+k, k, 0);
bitonicMerge(a,low, cnt, dir);
}
}
public static void sort(int[] a, int N, int up)
{
bitonicSort(a,0, N, up);
}
static void Main()
{
int[] a= {3, 7, 4, 8, 6, 2, 1, 5};
int N = a.Length;
int up = 1;
sort(a, N, up);
Console.Write("Sorted array: \n");
for (int i=0; i<N; i++)
Console.Write(a[i] + " ");
}
}
|
Javascript
<script>
function compAndSwap(a, i, j, dir) {
if ((a[i] > a[j] && dir === 1) ||
(a[i] < a[j] && dir === 0))
{
var temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
function bitonicMerge(a, low, cnt, dir) {
if (cnt > 1) {
var k = parseInt(cnt / 2);
for (var i = low; i < low + k; i++)
compAndSwap(a, i, i + k, dir);
bitonicMerge(a, low, k, dir);
bitonicMerge(a, low + k, k, dir);
}
}
function bitonicSort(a, low, cnt, dir) {
if (cnt > 1) {
var k = parseInt(cnt / 2);
bitonicSort(a, low, k, 1);
bitonicSort(a, low + k, k, 0);
bitonicMerge(a, low, cnt, dir);
}
}
function sort(a, N, up) {
bitonicSort(a, 0, N, up);
}
function printArray(arr) {
var n = arr.length;
for (var i = 0; i < n; ++i)
document.write(arr[i] + " ");
document.write("<br>");
}
var a = [3, 7, 4, 8, 6, 2, 1, 5];
var up = 1;
sort(a, a.length, up);
document.write("Sorted array: <br>");
printArray(a);
</script>
|
Output:
Sorted array:
1 2 3 4 5 6 7 8
Analysis of Bitonic Sort
To form a sorted sequence of length n from two sorted sequences of length n/2, log(n) comparisons are required.
For example: log(8) = 3 when sequence size. Therefore, The number of comparisons T(n) of the entire sorting is given by:
T(n) = log(n) + T(n/2)
The solution of this recurrence equation is
T(n) = log(n) + log(n)-1 + log(n)-2 + ... + 1 = log(n) · (log(n)+1) / 2
As each stage of the sorting network consists of n/2 comparators. Therefore total O(n log2n) comparators.
Time complexity:
- Best Case: O(log2n)
- Average Case: O(log2n)
- Worst Case: O(log2n)
Space Complexity: O(n.log2n)
Stable: Yes
Important Points:
- It is a comparison-based sorting technique
- Elements are sorted depending on the bitonic sequence
- Easily Implemented in parallel computing
- More efficient than quicksort
- The number of comparisons is more than other algorithms
- A sequence with elements in increasing and decreasing order is a bitonic sequence.
- Memory is well handled by the process.
- Best suited for parallel processor array.
Share your thoughts in the comments
Please Login to comment...