Biclustering in Data Mining

In recent days there is a tremendous development in technology. With recent technological advances in such areas as IT and biomedicine, many are facing issues in extracting of required data from the huge volume of data. These modern computers can produce and store unlimited data. So the problem of partitioning objects into no groups can be met in many areas. The vector partitioning problems consist of the partitioning of n-dimensional vectors into p-parts, these problems are mainly in data mining

“Data mining is a board area convening variety of methodologies for analyzing and modeling large data”

Analyzing patterns to partition the data samples according to some criteria is called clustering. The data mining technique which allows simultaneous clustering of the rows and columns of a matrix is called biclustering. A set of m samples represented by an n-dimensional feature vector, the entire dataset can be represented as m rows in an n column the biclustering algorithm generates biclusters, a subset of rows that exhibits similar behavior across a subset of columns. A biclustering of a dataset is a collection of pairs of sample and feature objects B=(l1, F1);(L2, F2); ……..(Lr, Fr) such that collection (L1, L2, L3……) forms a partitioning of a set of samples, and collections (F1, F2, F3….) form a partition of the set of features. A set of (Lk, Fk) will be a bicluster.

Types of Biclusters:

• Biclusters with a constant value:  It reorders rows and columns to group similar rows and columns with similar values, constant. A perfect constant bicluster is a matrix having all values equal.

20.0	20.0	20.0	20.0	20.0
20.0	20.0	20.0	20.0	20.0
20.0	20.0	20.0	20.0	20.0
20.0	20.0	20.0	20.0	20.0
20.0	20.0	20.0	20.0	20.0

• Bicluster with constant values on rows or columns: In these biclusters, rows, and columns should be normalized. 
• Bicluster with constant values on rows:

20.0	20.0	20.0	20.0	20.0
21.0	21.0	21.0	21.0	21.0
22.0	22.0	22.0	22.0	22.0
23.0	23.0	23.0	23.0	23.0
24.0	24.0	24.0	24.0	24.0

• Bicluster with constant value on columns:

20.0	21.0	22.0	23.0	24.0
20.0	21.0	22.0	23.0	24.0
20.0	21.0	22.0	23.0	24.0
20.0	21.0	22.0	23.0	24.0
20.0	21.0	22.0	23.0	24.0

• Bicluster with coherent values: The subsets of rows or columns will almost have the same score.
• Additive:

1.0	4.0	5.0	0.0	1.5
4.0	7.0	8.0	3.0	4.5
3.0	6.0	7.0	2.0	3.5
5.0	8.0	9.0	4.0	5.5
2.0	5.0	6.0	1.0	2.5

• Multiplicative:

1.0	0.5	2.0	0.2	0.8
2.0	1.0	4.0	0.4	1.6
3.0	1.5	6.0	0.6	2.4
4.0	2.0	8.0	0.8	3.2
5.2	2.5	10.0	1.0	4.0

• Unusually high/low values: In these matrices, we can have decimals, integers, etc, and in the top left 4 values are negative, and the bottom right 4 values are positive.

-10	-10	0.1	0.1
-10	-10	0.2	0.3
0.3	0.2	10	10
0.3	0.2	10	10

• Submatrices with low variance: In the matrix v , the values in v11,v12,v13,v14,v21,v31,v41 will be from 0.0 to 0.8. The values in v22,v23,v32,v33,v42,v43 will be from 0.1 to 0.2.

0.5	0.5	0.0	0.0
0.5	0.1	0.2	0.7
0.8	0.2	0.2	0.7
0.8	0.1	0.1	0.9

Bi-Partite Graph:

A vertex set divides into two disjoint sets v1,v2 and each edge in the graph joins a vertex in v1 to the vertex v2.

Row/Column	C1	C2	C3	C4
R1	0.1	0.0	0.0	0.2
R2	0.5	0.0	0.0	0.3
R3	0.0	0.2	0.1	0.0
R4	0.0	0.2	0.0	0.2

Spectral Co-Clustering:

Takes inputs as a bipartite graph, the data divides into a set of nodes and connected by edges. It finds biclusters with higher values and rearranges the matrix with higher values along the diagonal columns.  

For Inputs Matrix Aij:  

An = R^-1/2*A*C^-1/2 
[R^-1/2  ------> diagonal matrix with entry  i summation j (Aij)
 C^-1/2 -------> diagonal matrix with entry i summation i (Aij)]

 For Singular Value Decomposition: 

An = U summation v^T ------> provides rows and columns of A, 
left singular vector gives row partition 
and right singular vector gives columns.
L = [log2K]

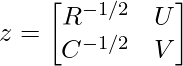
Spectral Biclustering:

It assumes the input matrix has a hidden keyboard structure. In this structure rows and columns are partitioned so that entries of any bicluster in the cartesian product of row clusters and column clusters are approximately constants.

Types of Normalization:

• Independent row and column normalization: This method makes the rows sum to a constant and sum of columns to a different constant.
• Bistochastization: This method makes the both rows and columns sum to the same constant.
• log normalization: The matrix is computed according to 

 kij = Lij – Li – Lj + L                       

Li=column; 

Lj=row;  

L=logA

Biclustering Evaluation:

To compare individual biclusters, The general formula is based on the Jaccard index:

   J(A,B) = | A interception B | / |A| + |B| – | A interception B |               

Where, A interception B means number of elements common to both A and B.

 If the Jaccard index is minimum when the biclusters do not overlap at all, the maximum occurs when they are identical. The  consensus  score ranges between o to 1.0

0-->min(good)
=> clusters are very well separated.

(all pairs of biclusters are totally dissimilar.

1.0-->max(not good) 
=> occurs when both sets are identical.