BFS for Disconnected Graph
Last Updated :
14 Sep, 2023
In the previous post, BFS only with a particular vertex is performed i.e. it is assumed that all vertices are reachable from the starting vertex. But in the case of a disconnected graph or any vertex that is unreachable from all vertex, the previous implementation will not give the desired output, so in this post, a modification is done in BFS.
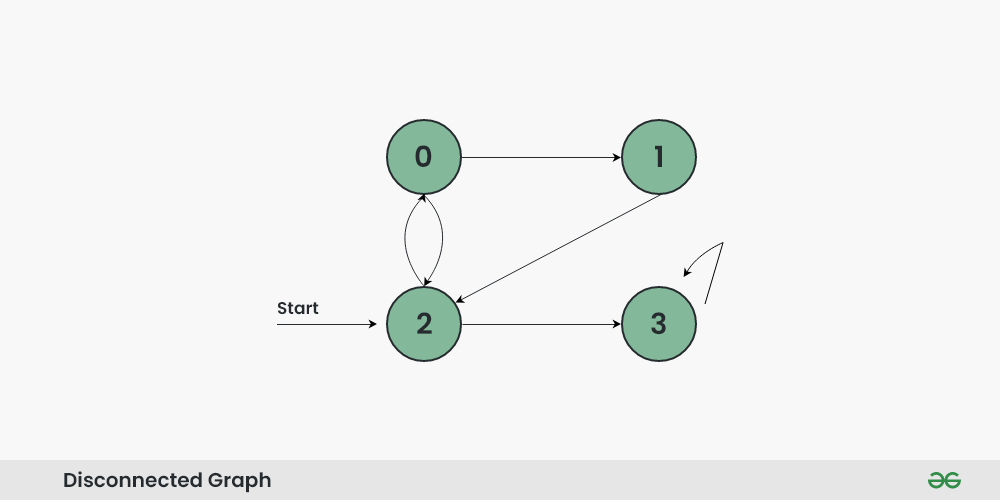
All vertices are reachable. So, for the above graph, simple BFS will work.
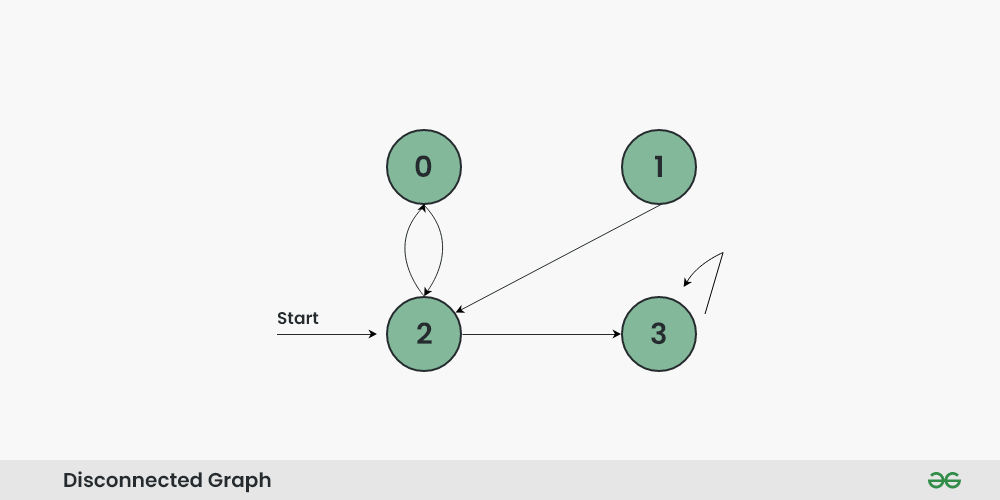
As in the above graph vertex 1 is unreachable from all vertex, so simple BFS wouldn’t work for it.
Just to modify BFS, perform simple BFS from each
unvisited vertex of given graph.
Following is the code when adjacency matrix representation is used for the graph.
C++
#include <iostream>
#include <queue>
using namespace std;
void printBFS(int** edges, int V, int start, int* visited);
void BFSHelper(int** edges, int V);
void addEdge(int** edges, int f, int s);
void addEdge(int** edges, int f, int s) { edges[f][s] = 1; }
void printBFS(int** edges, int V, int start, int* visited)
{
if (V == 0)
return;
queue<int> BFS;
BFS.push(start);
visited[start] = 1;
while (!BFS.empty()) {
int data = BFS.front();
BFS.pop();
cout << data << " ";
for (int i = 0; i < V; i++) {
if (edges[data][i] == 1) {
if (visited[i] == 0) {
BFS.push(i);
visited[i] = 1;
}
}
}
}
}
void BFSHelper(int** edges, int V)
{
if (V == 0)
return;
int* visited = new int[V];
for (int i = 0; i < V; i++) {
visited[i] = 0;
}
for (int i = 0; i < V; i++) {
if (visited[i] == 0) {
printBFS(edges, V, i, visited);
}
}
}
int main()
{
int V = 5;
int E = 6;
if (E == 0) {
for (int i = 0; i < V; i++) {
cout << i << " ";
}
return 0;
}
int** edges = new int*[V];
for (int i = 0; i < V; i++) {
edges[i] = new int[V];
for (int j = 0; j < V; j++) {
edges[i][j] = 0;
}
}
addEdge(edges, 0, 4);
addEdge(edges, 1, 2);
addEdge(edges, 1, 3);
addEdge(edges, 1, 4);
addEdge(edges, 2, 3);
addEdge(edges, 3, 4);
BFSHelper(edges, V);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static void addEdge(int[][] edges, int f, int s)
{
edges[f][s] = 1;
}
static void printBFS(int[][] edges, int V, int start,
int[] visited)
{
if (V == 0)
return;
Queue<Integer> BFS = new LinkedList<Integer>();
BFS.add(start);
visited[start] = 1;
while (!BFS.isEmpty()) {
int data = BFS.poll();
System.out.print(data + " ");
for (int i = 0; i < V; i++) {
if (edges[data][i] == 1) {
if (visited[i] == 0) {
BFS.add(i);
visited[i] = 1;
}
}
}
}
}
static void bfsHelper(int[][] edges, int V)
{
if (V == 0)
return;
int[] visited = new int[V];
for (int i = 0; i < V; i++) {
visited[i] = 0;
}
for (int i = 0; i < V; i++) {
if (visited[i] == 0) {
printBFS(edges, V, i, visited);
}
}
System.out.println();
}
public static void main(String[] args)
{
int V = 5;
int E = 6;
if (E == 0) {
for (int i = 0; i < V; i++) {
System.out.print(i + " ");
}
System.out.println();
System.exit(0);
}
int[][] edges = new int[V][V];
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
edges[i][j] = 0;
}
}
addEdge(edges, 0, 4);
addEdge(edges, 1, 2);
addEdge(edges, 1, 3);
addEdge(edges, 1, 4);
addEdge(edges, 2, 3);
addEdge(edges, 3, 4);
bfsHelper(edges, V);
}
}
|
Python3
import queue
def add_edge(edges, f, s):
edges[f][s] = 1
def print_bfs(edges, V, start, visited):
if V == 0:
return
bfs = queue.Queue()
bfs.put(start)
visited[start] = 1
while not bfs.empty():
data = bfs.get()
print(data, end=' ')
for i in range(V):
if edges[data][i] == 1:
if visited[i] == 0:
bfs.put(i)
visited[i] = 1
def bfs_helper(edges, V):
if V == 0:
return
visited = [0] * V
for i in range(V):
if visited[i] == 0:
print_bfs(edges, V, i, visited)
if __name__ == "__main__":
V = 5
E = 6
if E == 0:
for i in range(V):
print(i, end=' ')
exit()
edges = [[0 for _ in range(V)] for _ in range(V)]
add_edge(edges, 0, 4)
add_edge(edges, 1, 2)
add_edge(edges, 1, 3)
add_edge(edges, 1, 4)
add_edge(edges, 2, 3)
add_edge(edges, 3, 4)
bfs_helper(edges, V)
|
C#
using System;
using System.Collections.Generic;
class Gfg {
static void AddEdge(int[, ] edges, int f, int s)
{
edges[f, s] = 1;
}
static void PrintBFS(int[, ] edges, int V, int start,
int[] visited)
{
if (V == 0)
return;
Queue<int> BFS = new Queue<int>();
BFS.Enqueue(start);
visited[start] = 1;
while (BFS.Count > 0) {
int data = BFS.Dequeue();
Console.Write(data + " ");
for (int i = 0; i < V; i++) {
if (edges[data, i] == 1) {
if (visited[i] == 0) {
BFS.Enqueue(i);
visited[i] = 1;
}
}
}
}
}
static void BFSHelper(int[, ] edges, int V)
{
if (V == 0)
return;
int[] visited = new int[V];
for (int i = 0; i < V; i++) {
visited[i] = 0;
}
for (int i = 0; i < V; i++) {
if (visited[i] == 0) {
PrintBFS(edges, V, i, visited);
}
}
Console.WriteLine();
}
static void Main(string[] args)
{
int V = 5;
int E = 6;
if (E == 0) {
for (int i = 0; i < V; i++) {
Console.Write(i + " ");
}
Console.WriteLine();
Environment.Exit(0);
}
int[, ] edges = new int[V, V];
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
edges[i, j] = 0;
}
}
AddEdge(edges, 0, 4);
AddEdge(edges, 1, 2);
AddEdge(edges, 1, 3);
AddEdge(edges, 1, 4);
AddEdge(edges, 2, 3);
AddEdge(edges, 3, 4);
BFSHelper(edges, V);
}
}
|
Javascript
class Queue {
constructor() {
this.items = [];
}
push(element) {
return this.items.push(element);
}
pop() {
if (this.items.length > 0) {
return this.items.shift();
}
}
front() {
return this.items[0];
}
empty() {
return this.items.length == 0;
}
}
function addEdge(edges, f, s) {
edges[f][s] = 1;
}
function printBFS(edges, V, start, visited) {
if (V == 0) return;
let BFS = new Queue();
BFS.push(start);
visited[start] = 1;
while (!BFS.empty()) {
data = BFS.front();
BFS.pop();
console.log(data);
for (let i = 0; i < V; i++) {
if (edges[data][i] == 1) {
if (visited[i] == 0) {
BFS.push(i);
visited[i] = 1;
}
}
}
}
}
function BFSHelper(edges, V) {
if (V == 0) return;
let visited = new Array(V);
for (let i = 0; i < V; i++) {
visited[i] = 0;
}
for (let i = 0; i < V; i++) {
if (visited[i] == 0) {
printBFS(edges, V, i, visited);
}
}
}
let V = 5;
let E = 6;
if (E == 0) {
for (let i = 0; i < V; i++) {
console.log(i);
}
}
let edges = Array.from(Array(V), () => new Array(V));
for (let i = 0; i < V; i++) {
for (let j = 0; j < V; j++) {
edges[i][j] = 0;
}
}
addEdge(edges, 0, 4);
addEdge(edges, 1, 2);
addEdge(edges, 1, 3);
addEdge(edges, 1, 4);
addEdge(edges, 2, 3);
addEdge(edges, 3, 4);
BFSHelper(edges, V);
|
The time complexity of this algorithm is O(V + E), where V is the number of vertices and E is the number of edges. This is because we traverse each vertex and each edge once.
The space complexity is O(V), since we use an array to store the visited vertices.
Following is the code when adjacency list representation is used for the graph.
C++
#include<bits/stdc++.h>
using namespace std;
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
}
void BFSUtil(int u, vector<int> adj[],
vector<bool> &visited)
{
list<int> q;
visited[u] = true;
q.push_back(u);
while(!q.empty())
{
u = q.front();
cout << u << " ";
q.pop_front();
for (int i = 0; i != adj[u].size(); ++i)
{
if (!visited[adj[u][i]])
{
visited[adj[u][i]] = true;
q.push_back(adj[u][i]);
}
}
}
}
void BFS(vector<int> adj[], int V)
{
vector<bool> visited(V, false);
for (int u=0; u<V; u++)
if (visited[u] == false)
BFSUtil(u, adj, visited);
}
int main()
{
int V = 5;
vector<int> adj[V];
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
BFS(adj, V);
return 0;
}
|
Java
import java.util.*;
public class graph
{
static HashMap<Integer,LinkedList<Integer>> graph=new HashMap<>();
public static void addEdge(int a,int b)
{
if(graph.containsKey(a))
{
LinkedList<Integer> l=graph.get(a);
l.add(b);
graph.put(a,l);
}
else
{
LinkedList<Integer> l=new LinkedList<>();
l.add(b);
graph.put(a,l);
}
}
public static void bfshelp(int s,ArrayList<Boolean> visited)
{
LinkedList<Integer> q=new LinkedList<>();
q.add(s);
visited.set(s,true);
while(!q.isEmpty())
{
int f=q.poll();
System.out.print(f+" ");
if(graph.containsKey(f))
{
Iterator<Integer> i=graph.get(f).listIterator();
while(i.hasNext())
{
int n=i.next();
if(!visited.get(n))
{
visited.set(n,true);
q.add(n);
}
}
}
}
}
public static void bfs(int vertex)
{
ArrayList<Boolean> visited=new ArrayList<Boolean>();
for(int i=0;i<vertex;i++)
{
visited.add(i,false);
}
for(int i=0;i<vertex;i++)
{
if(!visited.get(i))
{
bfshelp(i,visited);
}
}
}
public static void main(String[] args)
{
int v=5;
addEdge(0, 4);
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 3);
addEdge(3, 4);
bfs(v);
}
}
|
Python3
import queue
def addEdge(adj, u, v):
adj[u].append(v)
def BFSUtil(u, adj, visited):
q = queue.Queue()
visited[u] = True
q.put(u)
while(not q.empty()):
u = q.queue[0]
print(u, end = " ")
q.get()
i = 0
while i != len(adj[u]):
if (not visited[adj[u][i]]):
visited[adj[u][i]] = True
q.put(adj[u][i])
i += 1
def BFS(adj, V):
visited = [False] * V
for u in range(V):
if (visited[u] == False):
BFSUtil(u, adj, visited)
if __name__ == '__main__':
V = 5
adj = [[] for i in range(V)]
addEdge(adj, 0, 4)
addEdge(adj, 1, 2)
addEdge(adj, 1, 3)
addEdge(adj, 1, 4)
addEdge(adj, 2, 3)
addEdge(adj, 3, 4)
BFS(adj, V)
|
C#
using System;
using System.Collections.Generic;
class Graph
{
static Dictionary<int,List<int>> graph =
new Dictionary<int,List<int>>();
public static void addEdge(int a, int b)
{
if(graph.ContainsKey(a))
{
List<int> l = graph[a];
l.Add(b);
if(graph.ContainsKey(a))
graph[a] = l;
else
graph.Add(a,l);
}
else
{
List<int> l = new List<int>();
l.Add(b);
graph.Add(a, l);
}
}
public static void bfshelp(int s, List<Boolean> visited)
{
List<int> q = new List<int>();
q.Add(s);
visited.RemoveAt(s);
visited.Insert(s,true);
while(q.Count != 0)
{
int f = q[0];
q.RemoveAt(0);
Console.Write(f + " ");
if(graph.ContainsKey(f))
{
foreach(int iN in graph[f])
{
int n = iN;
if(!visited[n])
{
visited.RemoveAt(n);
visited.Insert(n, true);
q.Add(n);
}
}
}
}
}
public static void bfs(int vertex)
{
List<Boolean> visited = new List<Boolean>();
for(int i = 0; i < vertex; i++)
{
visited.Insert(i, false);
}
for(int i = 0; i < vertex; i++)
{
if(!visited[i])
{
bfshelp(i, visited);
}
}
}
public static void Main(String[] args)
{
int v = 5;
addEdge(0, 4);
addEdge(1, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 3);
addEdge(3, 4);
bfs(v);
}
}
|
Javascript
class Graph {
constructor() {
this.graph = new Map();
}
addEdge(a, b) {
if (this.graph.has(a)) {
let l = this.graph.get(a);
l.push(b);
this.graph.set(a, l);
} else {
this.graph.set(a, [b]);
}
}
bfshelp(s, visited) {
let q = [];
q.push(s);
visited[s] = true;
while (q.length > 0) {
let f = q.shift();
console.log(f + " ");
if (this.graph.has(f)) {
let l = this.graph.get(f);
for (let n of l) {
if (!visited[n]) {
visited[n] = true;
q.push(n);
}
}
}
}
}
bfs(vertex) {
let visited = Array(vertex).fill(false);
for (let i = 0; i < vertex; i++) {
if (!visited[i]) {
this.bfshelp(i, visited);
}
}
}
}
let g = new Graph();
let v = 5;
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.bfs(v);
|
The time complexity of the given BFS algorithm is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
The space complexity is also O(V + E) since we need to store the adjacency list and the visited array.
Share your thoughts in the comments
Please Login to comment...