Angle between a chord and a tangent when angle in the alternate segment is given
Last Updated :
30 May, 2022
Given a circle whose chord and tangent meet at a particular point. The angle in the alternate segment is given. The task here is to find the angle between the chord and the tangent.
Examples:
Input: z = 48
Output: 48 degrees
Input: z = 64
Output: 64 degrees
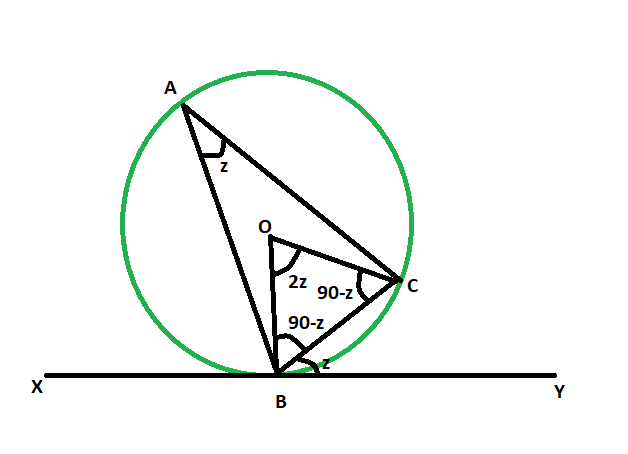
Approach:
- Let, angle BAC is the given angle in the alternate segment.
- let, the angle between the chord and circle = angle CBY = z
- as line drawn from center on the tangent is perpendicular,
- so, angle OBC = 90-z
- as, OB = OC = radius of the circle
- so, angle OCB = 90-z
- now, in triangle OBC,
angle OBC + angle OCB + angle BOC = 180
angle BOC = 180 – (90-z) – (90-z)
angle BOC = 2z - as angle at the circumference of a circle is half the angle at the centre subtended by the same arc,
so, angle BAC = z - hence, angle BAC = angle CBY

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void anglechordtang(int z)
{
cout << "The angle between tangent"
<< " and the chord is "
<< z << " degrees" << endl;
}
int main()
{
int z = 48;
anglechordtang(z);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void anglechordtang(int z)
{
System.out.print( "The angle between tangent"
+ " and the chord is "
+ z + " degrees");
}
public static void main (String[] args)
{
int z = 48;
anglechordtang(z);
}
}
|
Python3
def anglechordtang(z):
print("The angle between tangent",
"and the chord is", z , "degrees");
z = 48;
anglechordtang(z);
|
C#
using System;
class GFG
{
static void anglechordtang(int z)
{
Console.WriteLine( "The angle between tangent"
+ " and the chord is "
+ z + " degrees");
}
public static void Main ()
{
int z = 48;
anglechordtang(z);
}
}
|
Javascript
<script>
function anglechordtang(z)
{
document.write( "The angle between tangent"
+ " and the chord is "
+ z + " degrees");
}
var z = 48;
anglechordtang(z);
</script>
|
Output: The angle between tangent and the chord is 48 degrees
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...