Algebra of Matrices

Last Updated : 31 Jan, 2024

Algebra of Matrices denotes the various algebraic operations performed on a matrix. It includes operations such as Addition, Subtraction, and Multiplication. Matrices the the arrangement of numbers or any other mathematical elements in the form of rectangular arrays.

In this article, we will learn the various algebraic operations performed on the matrices, and solve some of the examples on the algebra of the matrices.

Table of Content

What is Algebra of Matrices?
Addition of Matrices
Subtraction of Matrices
Multiplication of Matrix
Transpose of Matrix
Negative of Matrix

What is Algebra of Matrices?

The various algebraic operation that can be performed on the matrix are collectively referred to as the algebra of the matrices.

The algebraic operations that can be performed on the matrices are namely:

Addition of Matrices
Subtraction of Matrices
Multiplication of Matrices
Transpose of Matrix
Negative of Matrix
Determinant of Matrix

Note: The division of matrices can be represented as the multiplication with the inverse of the matrix.

Learn, Matrices

Addition of Matrices

Addition of matrices is the summing of all the given matrices to obtain a single matrix after the operation. The operation is performed on the matrices (plural of matrix), such that element (say a_ij) in the resultant matrix at some position (say i and j) is equal to the addition operation performed on the elements at same position (i, j) of all the matrix.

Suppose we have n matrices, M1, M2, M3_,M4_,M5_…..upto M_n, and addition operation is performed on them and result is stored in R matrix, then for all the elements in R ( R_ij, where i is the row number and j is the column number of the element in the matrix R) can be individually represented as,

R_ij= M1_ij + M2_ij + M2_ij + …………….. Mn_ij

where,

R_ij is Element in matrix R at i^th row and j^th column and,
Mk_ijDenotes the element in M_k matrix at i^th row and j^th column.

Since every element is result of the operation performed on element at same position in all the matrices, thus the iff (if and only if) condition for addition of matrix is that the number of rows and columns in the all the involved matrices should be same, or in other terms the order of all the matrices should be same. Also the resultant matrix obtained after the operation is of the same order as of the involved matrices.

Example: Find the sum of the matrices when the given matrices are, $A = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix} and B = \begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$ .

Solution:

R = A + B

$R = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix} + \begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$

$R = \begin{bmatrix} a_{11}+b_{11} && a_{12}+b_{12} \\ a_{21}+b_{21} && a_{22}+b_{22} \end{bmatrix}$

Properties of Matrix Addition

Consider the A, B and C as there matrices and O is the zero matrix of same dimensions then the following properties hold:

Commutative Property: A + B = B + A
Associative Property: A + ( B + C) = (A + B) + C
Distributive Property: A x ( B + C ) = AB + AC
Additive Identity Property: A + O = A ‍
Additive Inverse Property: A + (-A) = O

Learn, Addition of Matrices

Subtraction of Matrices

Subtraction of matrices is the operation defined on the matrix to obtain a single matrix by subtracting corresponding elements of the two matrices. The two matrices which undergoes subtraction should be of same order and the resultant matrix is also of the same order.

Example: Find the difference between two matrices given as when the given matrices are, A = $A = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix}$ and $B = \begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$

Solution:

R = A – B

$R = \begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix} - \begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$

R = $\begin{bmatrix} a_{11}-b_{11} && a_{12}-b_{12} \\ a_{21}-b_{21} && a_{22}-b_{22} \end{bmatrix}$

Properties of Matrix Subtraction

Consider the A, B and C as there matrices and O is the zero matrix of same dimensions then the following properties hold:

Commutative Property: A – B ≠ B – A
Associative Property: A – ( B – C) ≠ (A – B) – C
Distributive Property: A ( B – C ) = AB – AC
Identity Property: A – O = A ‍
Additive Inverse Property: A – A = O

Multiplication of Matrix

Matrix multiplication is the operation operation performed on a set of matrices or with a set of matrices and a number to obtain a single matrix of order different from the involved matrices. The matrix multiplication can further have two ways based on whether the multiplication is with another matrix or a number.

Scalar Multiplication of Matrices

When the matrix is multiplied with a scalar quantity it is called scalar multiplication, and the resultant is a singular matrix of same dimension (rows and columns) just all the elements are multiplied with that scalar quantity.

Example: Given k and a matrix A $\begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix}$ . Find the value of kA.

Solution:

$R = x \times A = x \times\begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix} = \begin{bmatrix} x \times a_{11} && x \times a_{12} \\ x \times a_{21} && x \times a_{22} \end{bmatrix}$

How to Multiply Two Matrices?

When two matrices are multiplied a resultant matrix with changed dimensions is obtained. In matrix multiplication the two matrices must follow the rule which is, the number of rows in the second matrix should be equal to the number of columns in the first matrix, i.e if we have two matrices A (dimension a₁ x b₁ ) and B (dimension a₂ x b₂), then A x B is only possible if and only if b₁= a₁and the resultant matrix will have a dimension of a₁ x b₂.

An element R_ij of the resultant matrix is the result of the multiplication and addition operation of the i th row in the first matrix with the j th column in the second i.e R_ij= A_i1× B_1j + A_i2 × B_2j + …. + A_in × B_nj

Example: Given matrix A = $\begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix}$ and matrix B = $\begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$ . What will be the result of A × B.

Solution:

R = A × B

R = $\begin{bmatrix} a_{11} && a_{12} \\ a_{21} && a_{22} \end{bmatrix} \times \begin{bmatrix} b_{11} && b_{12} \\ b_{21} && b_{22} \end{bmatrix}$

R = $\begin{bmatrix} a_{11}\times b_{11} + a_{12} \times b_{21} && a_{11}\times b_{12} + a_{12}\times b_{22}\\ a_{21}\times b_{11} + a_{22}\times b_{21} && a_{21}\times b_{12} + a_{22}\times b_{22} \end{bmatrix}$

Properties of Matrix Multiplication

Consider the A, B and C as there matrices and O is the zero matrix of same dimensions then the following properties hold:

Commutative Property: AB 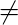$\neq$ BA ( not commutative )
Associative Property: A × ( B × C ) = ( A × B ) × C
Distributive Property: A × ( B + C ) = AB + AC
Multiplicative Identity Property: A × I = A ( or I × A = A )
Multiplicative Property of Zero: A x O = O ( or O × A = O )

Learn, Matrix Multiplication

Transpose of Matrix

When the rows and columns of matrix are swapped, i.e the row will now become column of the matrix and the column will now become row, the then obtained matrix is called transpose of the original matrix.

It is denoted by A^T , where A is the original matrix.

Note: If the order of the original matrix is m x n, then the dimension of the transpose matrix will be n x m.

If we have a matrix $A = \begin{bmatrix} a_{11} && a_{12} && a_{13}\\ a_{21} && a_{22} && a_{23} \\ a_{31} && a_{32} && a_{33}\end{bmatrix}$ , then the transpose matrix A^Twill be,

$A^T = \begin{bmatrix} a_{11} && a_{21} && a_{31} \\ a_{12}&&a_{22}&&a_{32} \\ a_{13}&&a_{23}&&a_{33}\end{bmatrix}$

Properties of Transpose of Matrix

|A^T| = |A|
(A^T )^T = A
(A + B)^T = A^T + B^T
(xA)^T = xA^T
(AB)^T = B^TA^T

Learn, Transpose of Matrix

Negative of Matrix

When each element of the original matrix is replaced by the negative of the element, the then obtained matrix is called negative of the original matrix.

Negative of the matrix is similar to scalar multiplication of the matrix with -1.

The negative of matrix is denoted by -A, where A is the original matrix.

If we have the matrix $A = \begin{bmatrix} a_{11} && a_{12} && a_{13}\\ a_{21} && a_{22} && a_{23} \\ a_{31} && a_{32} && a_{33}\end{bmatrix}$ , then the negative of the matrix will be,

$-A = \begin{bmatrix} -a_{11} && -a_{12} && -a_{13}\\ -a_{21} && -a_{22} && -a_{23} \\ -a_{31} && -a_{32} && -a_{33}\end{bmatrix}$

Properties of Negative of Matrix

| -A | = | A |
(-A)^T = – A^T

Determinant of Matrix

Determinant of Matrix is a scalar value calculated for a given matrix.

It is represented by det(A) or | A |, where A is the original matrix.

Note: The determinant is defined only for the square matrix i.e is the matrix in which the number of rows and columns are equal.

Determinant of a 2×2 Matrix

If we have a 2×2 matrix $A = \begin{bmatrix} a&b\\c&d \end{bmatrix}$ , the

|A| = ac – bd

Determinant of a 3×3 Matrix

If we have a 3×3 matrix $A = \begin{bmatrix} a&b&c\\ d&e&f\\g&h&i \end{bmatrix}$ , then

| A | = a(ei – fh) – b(di – fg) + c(dh – eg)

How to Calculate Determinant?

For each element of the first row or first column get the cofactor of those elements. Cofactor matrix of any element is defined as the matrix formed by removing the row and column of the element from the original matrix.
Then multiply the element with the determinant of the corresponding cofactor.
Finally, add them with alternate signs such the no two consecutive signs are same starting as positive from top left. As a base case, the value of the determinant of a 1*1 matrix is the single value itself.

Learn, Determinant of Matrix

Symmetric Matrix

Symmetric Matrix are those matrix which has its transpose equal to it.

These matrices are symmetric about the main diagonal of the matrix and are defined for the square matrices only.

For symmetric matrix we can say that,

A^T = A

where

A is the original matrix
A^Tdenotes the transpose of the original matrix.

Example of symmetric matrix:

$A = \begin{bmatrix} x&a&b \\ a&y&c \\ b&c&z \end{bmatrix}$

Skew-Symmetric Matrix

A skew symmetric matrix is a special type of square matrix in which transpose of matrix is equal to the negative of the original matrix.

Learn, Symmetric and Skew Symmetric Matrix

Conditions for any matrix to be skew-symmetric:

Must be a square matrix.
All the elements along the main diagonal must be equal to zero.
The determinant of the matrix must be zero i.e | A| = 0

For skew-symmetric matrix we can say that:

A^T = -A

where,

A is the original matrix ,
A^T is the transpose of the matrix and,
-A is the negative of the matrix.

Example of skew-symmetric matrix:

$A = \begin{bmatrix} 0&a&b \\ -a&0&c \\ -b&-c&0\end{bmatrix}$

Related Reads

Solved Examples of Algebra of Matrices

Example 1: Given a matrix A_3×3 = $\begin{bmatrix} 1 && 3 && 5\\ 7 && 9 && 11 \\ 13 && 15 && 17 \end{bmatrix}$ and B_3×3 = $\begin{bmatrix} 2 && 4 && 6 \\ 8 && 10 && 12 \\ 14 && 16 && 18 \end{bmatrix}$ what will be the resultant matrix when addition is performed on these two matrices ?

Solution:

Let the R be the resultant matrix, then

R = A + B

R = $\begin{bmatrix} 1 && 3 && 5 \\ 7 && 9 && 11 \\ 13 && 15 && 17 \end{bmatrix} + \begin{bmatrix} 2 && 4 && 6\\ 8 && 10 && 12 \\ 14 && 16 && 18 \end{bmatrix}$

R = $= \begin{bmatrix} 1+2 && 3+4 && 5+6 \\ 7+8 && 9+10 && 11+12 \\ 13+14 && 15+16 && 17+18 \end{bmatrix}$

R = $\begin{bmatrix} 3 && 7 && 11 \\ 15 && 10 && 23 \\ 27 && 31 && 35 \end{bmatrix}$

Example 2: Given a matrix A_2×2 = $\begin{bmatrix} 1 && 3\\ 5 && 7 \end{bmatrix}$ and B_2×2 = $\begin{bmatrix} 2 && 4 \\ 6 && 8 \end{bmatrix}$ what will be the resultant matrix when addition is performed on these two matrices ?

Solution:

Let the R be the resultant matrix, then

R = A – B

R = $\begin{bmatrix} 1 && 3 \\ 5 && 7 \end{bmatrix} - \begin{bmatrix} 2 && 4 \\ 6&&8\end{bmatrix}$

R = $\begin{bmatrix} 1-2 && 3-4 \\ 5-6 && 7-8 \end{bmatrix}$

R = $\begin{bmatrix} -1 && -1 \\ -1 && -1 \end{bmatrix}$

Example 3: Given k = 2 and matrix A = $\begin{bmatrix} 1 && 2 && 4 \\ 3 && 6 && 9 \end{bmatrix}$ is given below, return the resultant matrix after performing scalar multiplication with k.

Solution:

The scalar multiplication can be given as:

R = kA

R = $\begin{bmatrix} 2\times1 && 2\times2 && 2\times4 \\ 2\times3 && 2\times6 && 2\times9 \end{bmatrix}$

R = $\begin{bmatrix} 2 && 4 && 8\\ 6 && 12 && 18 \end{bmatrix}$

Example 4: Given a matrix A_{2×3 =} $\begin{bmatrix} 1&&2&&3 \\ 4&&5&&6 \end{bmatrix}$ and B_{3×2 =} $\begin{bmatrix}1&&2 \\ 3&&4 \\ 5&&6 \end{bmatrix}$ what will be the resultant matrix when multiplication is performed on these two matrices ?

Solution:

Let R represents the result of the matrix multiplication, then

R = A × B

R = $\begin{bmatrix} 1&&2&&3 \\ 4&&5&&6 \end{bmatrix} \times \begin{bmatrix}1&&2 \\ 3&&4 \\ 5&&6 \end{bmatrix}$

R = $\begin{bmatrix} 1\times1+2\times3+3\times5 && 1\times2+2\times4+3\times6 \\ 4\times1+5\times3+6\times5 && 4\times2+5\times4+6\times6\end{bmatrix}$

R = $\begin{bmatrix} 22&&28 \\49&&64\end{bmatrix}$

Example 5: Calculate the determinant of matrix $A = \begin{bmatrix} 1&2\\3&4\end{bmatrix}$ .

Solution:

|A| = 1 × 4 – 2 × 3 = 4 – 6 = -2