8085 program to find square of a 8 bit number

Problem – Write an assembly language program in 8085 microprocessor to find square of 8 bit number. Example – 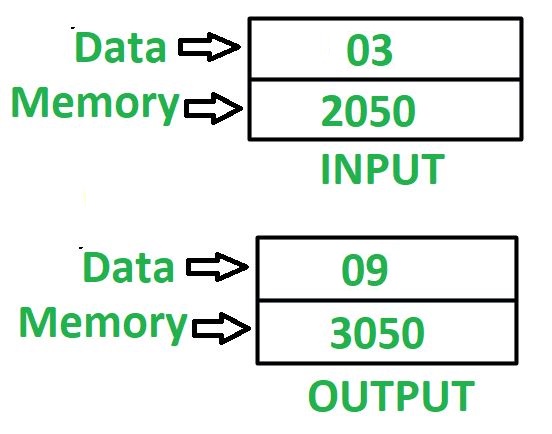Assumption – Addresses of input data and out data are 2050 and 3050 respectively. Approach – Combine the content of registers H and L, the resultant content can be used to indirectly point to memory location and that memory location is specified by M. To find square of any number, keep on adding that number in accumulator A which initially contains 0 by that number of times whose square we need to find. Algorithm –

1. Assign 20 to register H, 50 to register L and 00 to accumulator A
2. Load the content of memory location which is specified by M in register B
3. Add content of M in accumulator A and decrement value of B by 01
4. Check if B holds 00, if true then store the value of A at memory location 3050 otherwise go to step 3

Program –

MEMORY ADDRESS	MNEMONICS	COMMENT
2000	MVI H 20	H <- 20
2002	MVI L 50	L <- 50
2004	MVI A 00	A <- 00
2006	MOV B, M	B <- M
2007	ADD M	A <- A + M
2008	DCR B	B <- B – 01
2009	JNZ 2007	Jump if ZF = 0
200C	STA 3050	M[3050] <- A
200F	HLT	END

Explanation – Registers used A, H, L, B and indirect memory M:

1. MVI H 20 – initialize register H with 20
2. MVI L 50 – initialize register L with 50
3. MVI A 00 – initialize accumulator A with 00
4. MOV B, M – moves the content of memory location which is indirectly specified by M in register B
5. ADD M – add the content of memory location which is indirectly specified by M in accumulator A
6. DCR B – decrement value of register B by 1
7. JNZ 2007 – jump to memory location 2007 if ZF = 0, i.e register B does not contain 0
8. STA 3050 – stores value of A in 3050
9. HLT – stops executing the program and halts any further execution

Advantages:

1. Simple and easy to understand logic
   
2. Uses only a few instructions, making it efficient in terms of memory usage and execution time
   
3. Can be easily modified to square larger numbers
   

Disadvantages:

1. Only works for 8-bit numbers
   
2. Can only find the square of positive numbers
   
3. May not be the most efficient method for finding the square of a number, especially for larger numbers. There are faster algorithms, such as the binary method or the Karatsuba algorithm, that can be used to find the square of a number more efficiently.