8085 program to find sum of digits of 8 bit number
Last Updated :
07 May, 2023
Problem: Write an assembly language program in 8085 microprocessor to find the sum of digits of an 8-bit number.
Example:
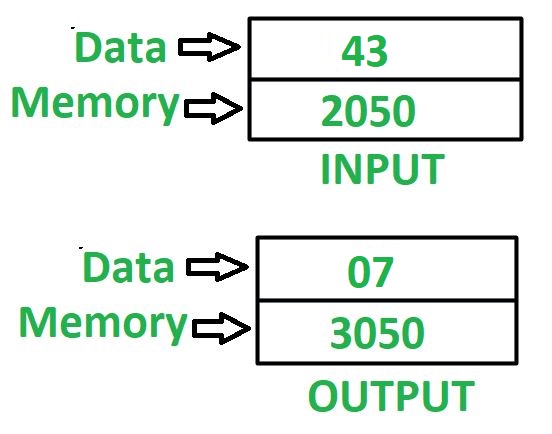
Assumptions: Addresses of input data and output data are 2050 and 3050 respectively.
Algorithm:
- Load value stored at memory location 2050 in accumulator A
- Move the value of accumulator A in register B to process 43H.
- Perform masking of nibbles i.e. do AND operation of accumulator A with OF with help of ANI (Immediate Addressing Mode with AND) instruction. We will get a lower nibble value in accumulator A. Because of 0F, Higher Nibble will be masked and a lower nibble will be obtained as it is.
- Move the value of accumulator A in register C, Because currently, the Accumulator value is the value of a lower nibble so [C] = Lower nibble value = 3H
- Move the value of register B in accumulator A, Because the value of the Accumulator is updated hence we will again move the Value of B into Accumulator.
- Reverse the number which is stored in accumulator A by using RLC instruction 4 times and again do masking of nibbles as done in step 3.
- Add the value of register C in accumulator A
- Store the value of A in memory location 3050
(After using 4 Times RLC, we will get reversed of given number because after 4 times, 4 bits will move left and again it will be rotated to MSB to LSB and vice-versa hence we will get reversed number, And after using ANI 0F, we will get Lower nibble values in both the cases. Hence after adding these 2 values using ADD C instruction, we are getting a sum of digits in a given number.)
Program –
| MEMORY ADDRESS |
MNEMONICS |
COMMENT |
| 2000 |
LDA 2050 |
A <- M[2050] |
| 2003 |
MOV B, A |
B <- A |
| 2004 |
ANI 0F |
A <- A (AND) 0F |
| 2006 |
MOV C, A |
C <- A |
| 2007 |
MOV A, B |
A <- B |
| 2008 |
RLC |
Rotate left without carry |
| 2009 |
RLC |
Rotate left without carry |
| 200A |
RLC |
Rotate left without carry |
| 200B |
RLC |
Rotate left without carry |
| 200C |
ANI 0F |
A <- A (AND) 0F |
| 200E |
ADD C |
A <- A + C |
| 200F |
STA 3050 |
M[3050] <- A |
| 2012 |
HLT |
END |
Advantages of finding the sum:
- It is a simple and useful mathematical operation that can be used in various applications, such as in checking the validity of credit card numbers or identifying patterns in numerical data.
- It can help reveal the properties and characteristics of a number, such as its divisibility or relationship to other numbers.
- It can be easily calculated using a loop or mathematical formula in a programming language, making it a versatile tool for solving problems.
Disadvantages of finding the sum:
- It may not be useful in certain contexts where the individual digits are not relevant or meaningful, such as in analyzing the frequencies of letters in a text.
- It may require specialized knowledge or software to handle large numbers, leading to computational complexity and potential errors.
- It may not be practical for numbers with many digits, as the number of digits to add up can become very large.
Explanation: Registers used A, B, C
- LDA 2050: loads the content of memory location 2050 in accumulator A
- MOV B, A: moves the value of accumulator A in register B
- ANI 0F: performs AND operation in value of accumulator A and 0F
- MOV C, A: moves the value of accumulator A in register C
- MOV A, B: moves the value of register B in accumulator A
- RLC: instruction rotates the value of accumulator A, left by 1 bit. Since it is performed 4 times therefore this will reverse the number i.e swaps the lower order nibble with a higher-order nibble
- Repeat step 3
- ADD C: Add the content of the register of C in accumulator A
- STA 3050: Stores value of A in 3050
- HLT: Stops executing the program and halts any further execution
ADDITIONAL INSTRUCTION: This task can be done in a 2nd way by using 4 times RRC instruction.
LDA 2050
ANI 0F
MOV C, A
MOV A, B
RRC
RRC //4 RRC do same work as 4 RLC. So we can use anyone alternatively.
RRC
RRC
ANI 0F
ADD C
STA 3050
HLT
END
Example :
16H in Binary Written as :
0001 0110
RLC 1st Time : 0010 1100 {Carry Flag = 0}
RLC 2nd Time : 0101 1000 {Carry Flag = 0}
RLC 3rd Time : 1011 0000 {Carry Flag = 0}
RLC 4th Time : 0110 0001 { Carry Flag = 1}
Converted Number after 4th RLC : 0110 0001 [61H]
Hence our number is reversed from 16H to 61H.
For Example : 16H in Binary Written as :
0001 0110
RRC 1st Time : 0000 1011 {Carry Flag = 0}
RRC 2nd Time : 1000 0101 {Carry Flag = 1}
RRC 3rd Time : 1100 0010 { Carry Flag = 1}
RRC 4th Time : 0110 0001 { Carry Flag = 0}
Converted Number after 4th RRC : 0110 0001 [61H]
Hence our number is reversed from 16H to 61H.
Hence Instead of 4 RLC, we can also use 4 RRC instructions in our code and
accordingly AND them with 0F in the same way as above.
Share your thoughts in the comments
Please Login to comment...