Queue using Stacks
Last Updated :
10 Jul, 2023
The problem is opposite of this post. We are given a stack data structure with push and pop operations, the task is to implement a queue using instances of stack data structure and operations on them.
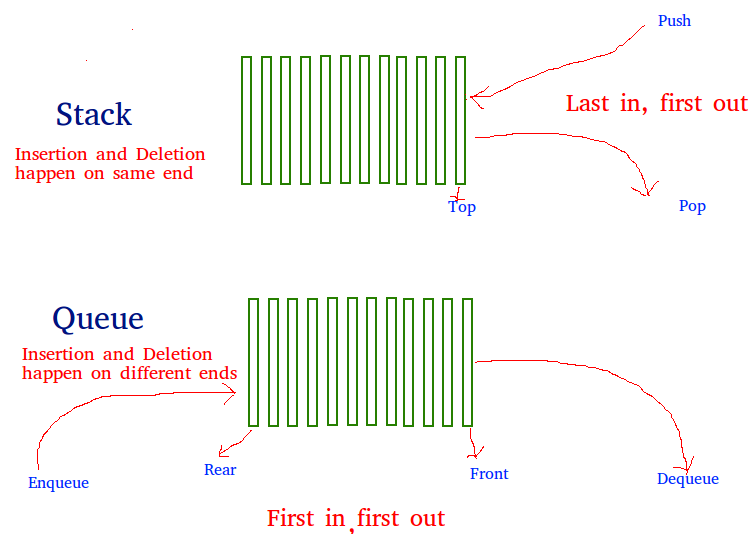
A queue can be implemented using two stacks. Let queue to be implemented be q and stacks used to implement q be stack1 and stack2. q can be implemented in two ways:
Method 1 (By making enQueue operation costly): This method makes sure that oldest entered element is always at the top of stack 1, so that deQueue operation just pops from stack1. To put the element at top of stack1, stack2 is used.
enQueue(q, x):
- While stack1 is not empty, push everything from stack1 to stack2.
- Push x to stack1 (assuming size of stacks is unlimited).
- Push everything back to stack1.
Here time complexity will be O(n)
deQueue(q):
- If stack1 is empty then error
- Pop an item from stack1 and return it
Here time complexity will be O(1)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
void enQueue(int x)
{
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
s1.push(x);
while (!s2.empty()) {
s1.push(s2.top());
s2.pop();
}
}
int deQueue()
{
if (s1.empty()) {
return -1;
}
int x = s1.top();
s1.pop();
return x;
}
};
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class Queue
{
static Stack<Integer> s1 = new Stack<Integer>();
static Stack<Integer> s2 = new Stack<Integer>();
static void enQueue(int x)
{
while (!s1.isEmpty())
{
s2.push(s1.pop());
}
s1.push(x);
while (!s2.isEmpty())
{
s1.push(s2.pop());
}
}
static int deQueue()
{
if (s1.isEmpty())
{
return -1;
}
int x = s1.peek();
s1.pop();
return x;
}
};
public static void main(String[] args)
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
System.out.println(q.deQueue());
System.out.println(q.deQueue());
System.out.println(q.deQueue());
}
}
|
Python3
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
def enQueue(self, x):
while len(self.s1) != 0:
self.s2.append(self.s1[-1])
self.s1.pop()
self.s1.append(x)
while len(self.s2) != 0:
self.s1.append(self.s2[-1])
self.s2.pop()
def deQueue(self):
if len(self.s1) == 0:
return -1;
x = self.s1[-1]
self.s1.pop()
return x
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
|
C#
using System;
using System.Collections;
class GFG
{
public class Queue
{
public Stack s1 = new Stack();
public Stack s2 = new Stack();
public void enQueue(int x)
{
while (s1.Count > 0)
{
s2.Push(s1.Pop());
}
s1.Push(x);
while (s2.Count > 0)
{
s1.Push(s2.Pop());
}
}
public int deQueue()
{
if (s1.Count == 0)
{
return -1;
}
int x = (int)s1.Peek();
s1.Pop();
return x;
}
};
public static void Main()
{
Queue q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue()+" ");
Console.Write(q.deQueue());
}
}
|
Javascript
<script>
class Queue{
constructor()
{
this.s1 = [];
this.s2 = [];
}
enQueue(x)
{
while (this.s1.length != 0)
{
this.s2.push(this.s1.pop());
}
this.s1.push(x);
while (this.s2.length != 0)
{
this.s1.push(this.s2.pop());
}
}
deQueue()
{
if (this.s1.length == 0)
{
return -1;
}
let x = this.s1[this.s1.length - 1];
this.s1.pop();
return x;
}
}
let q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
document.write(q.deQueue() + "<br>");
document.write(q.deQueue() + "<br>");
document.write(q.deQueue() + "<br>");
</script>
|
Output:
1
2
3
Complexity Analysis:
- Time Complexity:
- Push operation: O(N).
In the worst case we have empty whole of stack 1 into stack 2. - Pop operation: O(1).
Same as pop operation in stack.
- Auxiliary Space: O(N).
Use of stack for storing values.
Method 2 (By making deQueue operation costly): In this method, in en-queue operation, the new element is entered at the top of stack1. In de-queue operation, if stack2 is empty then all the elements are moved to stack2 and finally top of stack2 is returned.
enQueue(q, x)
1) Push x to stack1 (assuming size of stacks is unlimited).
Here time complexity will be O(1)
deQueue(q)
1) If both stacks are empty then error.
2) If stack2 is empty
While stack1 is not empty, push everything from stack1 to stack2.
3) Pop the element from stack2 and return it.
Here time complexity will be O(n)
Method 2 is definitely better than method 1.
Method 1 moves all the elements twice in enQueue operation, while method 2 (in deQueue operation) moves the elements once and moves elements only if stack2 empty. So, the amortized complexity of the dequeue operation becomes 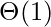
Implementation of method 2:
C++
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s1, s2;
void enQueue(int x)
{
s1.push(x);
}
int deQueue()
{
if (s1.empty() && s2.empty()) {
return -1;
}
if (s2.empty()) {
while (!s1.empty()) {
s2.push(s1.top());
s1.pop();
}
}
int x = s2.top();
s2.pop();
return x;
}
};
int main()
{
Queue q;
cout << q.deQueue() << '\n';
q.enQueue(1);
cout << q.deQueue() << '\n';
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct sNode {
int data;
struct sNode* next;
};
void push(struct sNode** top_ref, int new_data);
int pop(struct sNode** top_ref);
struct queue {
struct sNode* stack1;
struct sNode* stack2;
};
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
int deQueue(struct queue* q)
{
int x;
if (q->stack1 == NULL && q->stack2 == NULL) {
return -1;
}
if (q->stack2 == NULL) {
while (q->stack1 != NULL) {
x = pop(&q->stack1);
push(&q->stack2, x);
}
}
x = pop(&q->stack2);
return x;
}
void push(struct sNode** top_ref, int new_data)
{
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
new_node->data = new_data;
new_node->next = (*top_ref);
(*top_ref) = new_node;
}
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
if (*top_ref == NULL) {
return -1;
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
int main()
{
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
q->stack2 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
|
Java
import java.util.Stack;
public class GFG {
static class Queue {
Stack<Integer> stack1;
Stack<Integer> stack2;
}
static void push(Stack<Integer> top_ref, int new_data)
{
top_ref.push(new_data);
}
static int pop(Stack<Integer> top_ref)
{
if (top_ref.isEmpty()) {
return -1;
}
return top_ref.pop();
}
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
static int deQueue(Queue q)
{
int x;
if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
return -1;
}
if (q.stack2.isEmpty()) {
while (!q.stack1.isEmpty()) {
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
public static void main(String args[])
{
Queue q = new Queue();
q.stack1 = new Stack<>();
q.stack2 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.println(deQueue(q) + " ");
}
}
|
Python3
class Queue:
def __init__(self):
self.s1 = []
self.s2 = []
def enQueue(self, x):
self.s1.append(x)
def deQueue(self):
if len(self.s1) == 0 and len(self.s2) == 0:
return -1
elif len(self.s2) == 0 and len(self.s1) > 0:
while len(self.s1):
temp = self.s1.pop()
self.s2.append(temp)
return self.s2.pop()
else:
return self.s2.pop()
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class Queue
{
public Stack<int> stack1;
public Stack<int> stack2;
}
static void push(Stack<int> top_ref, int new_data)
{
top_ref.Push(new_data);
}
static int pop(Stack<int> top_ref)
{
if (top_ref.Count == 0)
{
return -1;
}
return top_ref.Pop();
}
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
static int deQueue(Queue q)
{
int x;
if (q.stack1.Count == 0 && q.stack2.Count == 0)
{
return -1;
}
if (q.stack2.Count == 0)
{
while (q.stack1.Count != 0)
{
x = pop(q.stack1);
push(q.stack2, x);
}
}
x = pop(q.stack2);
return x;
}
public static void Main(String []args)
{
Queue q = new Queue();
q.stack1 = new Stack<int>();
q.stack2 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.WriteLine(deQueue(q) + " ");
}
}
|
Javascript
<script>
class Queue {
constructor() {
this.s1 = [];
this.s2 = [];
}
enQueue(x) {
this.s1.push(x);
}
deQueue() {
if (this.s1.length == 0 && this.s2.length == 0) {
return -1;
}
if (this.s2.length == 0) {
while (this.s1.length != 0) {
this.s2.push(this.s1[0]);
this.s1.shift();
}
}
let x = this.s2[0];
this.s2.shift();
return x;
}
};
let q = new Queue;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
console.log(q.deQueue());
console.log(q.deQueue());
console.log(q.deQueue());
</script>
|
Output:
1 2 3
Complexity Analysis:
- Time Complexity:
- Push operation: O(1).
Same as pop operation in stack. - Pop operation: O(N) in general and O(1) amortized time complexity.
In the worst case we have to empty the whole of stack 1 into stack 2 so its O(N). Amortized time is the way to express the time complexity when an algorithm has the very bad time complexity only once in a while besides the time complexity that happens most of time. So its O(1) amortized time complexity, since we have to empty whole of stack 1 only when stack 2 is empty, rest of the times the pop operation takes O(1) time.
- Auxiliary Space: O(N).
Use of stack for storing values.
Queue can also be implemented using one user stack and one Function Call Stack. Below is modified Method 2 where recursion (or Function Call Stack) is used to implement queue using only one user defined stack.
enQueue(x)
1) Push x to stack1.
deQueue:
1) If stack1 is empty then error.
2) If stack1 has only one element then return it.
3) Recursively pop everything from the stack1, store the popped item
in a variable res, push the res back to stack1 and return res
The step 3 makes sure that the last popped item is always returned and since the recursion stops when there is only one item in stack1 (step 2), we get the last element of stack1 in deQueue() and all other items are pushed back in step
3. Implementation of method 2 using Function Call Stack:
C++
#include <bits/stdc++.h>
using namespace std;
struct Queue {
stack<int> s;
void enQueue(int x)
{
s.push(x);
}
int deQueue()
{
if (s.empty()) {
return -1;
}
int x = s.top();
s.pop();
if (s.empty())
return x;
int item = deQueue();
s.push(x);
return item;
}
};
int main()
{
Queue q;
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
cout << q.deQueue() << '\n';
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
struct sNode {
int data;
struct sNode* next;
};
struct queue {
struct sNode* stack1;
};
void push(struct sNode** top_ref, int new_data);
int pop(struct sNode** top_ref);
void enQueue(struct queue* q, int x)
{
push(&q->stack1, x);
}
int deQueue(struct queue* q)
{
int x, res;
if (q->stack1 == NULL) {
return -1;
}
else if (q->stack1->next == NULL) {
return pop(&q->stack1);
}
else {
x = pop(&q->stack1);
res = deQueue(q);
push(&q->stack1, x);
return res;
}
}
void push(struct sNode** top_ref, int new_data)
{
struct sNode* new_node = (struct sNode*)malloc(sizeof(struct sNode));
if (new_node == NULL) {
printf("Stack overflow \n");
getchar();
exit(0);
}
new_node->data = new_data;
new_node->next = (*top_ref);
(*top_ref) = new_node;
}
int pop(struct sNode** top_ref)
{
int res;
struct sNode* top;
if (*top_ref == NULL) {
return -1;
}
else {
top = *top_ref;
res = top->data;
*top_ref = top->next;
free(top);
return res;
}
}
int main()
{
struct queue* q = (struct queue*)malloc(sizeof(struct queue));
q->stack1 = NULL;
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
printf("%d ", deQueue(q));
return 0;
}
|
Java
import java.util.Stack;
public class QOneStack {
static class Queue {
Stack<Integer> stack1;
}
static void push(Stack<Integer> top_ref, int new_data)
{
top_ref.push(new_data);
}
static int pop(Stack<Integer> top_ref)
{
if (top_ref == null) {
return -1;
}
return top_ref.pop();
}
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
static int deQueue(Queue q)
{
int x, res = 0;
if (q.stack1.isEmpty()) {
return -1;
}
else if (q.stack1.size() == 1) {
return pop(q.stack1);
}
else {
x = pop(q.stack1);
res = deQueue(q);
push(q.stack1, x);
return res;
}
}
public static void main(String[] args)
{
Queue q = new Queue();
q.stack1 = new Stack<>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
System.out.print(deQueue(q) + " ");
}
}
|
Python3
class Queue:
def __init__(self):
self.s = []
def enQueue(self, data):
self.s.append(data)
def deQueue(self):
if len(self.s) <= 0:
return -1
x = self.s[len(self.s) - 1]
self.s.pop()
if len(self.s) <= 0:
return x
item = self.deQueue()
self.s.append(x)
return item
if __name__ == '__main__':
q = Queue()
q.enQueue(1)
q.enQueue(2)
q.enQueue(3)
print(q.deQueue())
print(q.deQueue())
print(q.deQueue())
|
C#
using System;
using System.Collections.Generic;
public class QOneStack
{
public class Queue
{
public Stack<int> stack1;
}
static void push(Stack<int> top_ref, int new_data)
{
top_ref.Push(new_data);
}
static int pop(Stack<int> top_ref)
{
if (top_ref == null)
{
return -1;
}
return top_ref.Pop();
}
static void enQueue(Queue q, int x)
{
push(q.stack1, x);
}
static int deQueue(Queue q)
{
int x, res = 0;
if (q.stack1.Count == 0)
{
return -1;
}
else if (q.stack1.Count == 1)
{
return pop(q.stack1);
}
else
{
x = pop(q.stack1);
res = deQueue(q);
push(q.stack1, x);
return res;
}
}
public static void Main(String[] args)
{
Queue q = new Queue();
q.stack1 = new Stack<int>();
enQueue(q, 1);
enQueue(q, 2);
enQueue(q, 3);
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
Console.Write(deQueue(q) + " ");
}
}
|
Javascript
class Queue {
constructor() {
this.s1 = [];
this.s2 = [];
}
enQueue(x) {
this.s1.push(x);
}
deQueue() {
if (this.s1.length == 0 && this.s2.length == 0) {
return -1;
}
if (this.s2.length == 0) {
while (this.s1.length != 0) {
this.s2.push(this.s1[0]);
this.s1.shift();
}
}
let x = this.s2[0];
this.s2.shift();
return x;
}
}
let q = new Queue();
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
console.log(q.deQueue());
console.log(q.deQueue());
console.log(q.deQueue());
|
Output:
1 2 3
Complexity Analysis:
- Time Complexity:
- Push operation : O(1).
Same as pop operation in stack. - Pop operation : O(N).
The difference from above method is that in this method element is returned and all elements are restored back in a single call.
- Auxiliary Space: O(N).
Use of stack for storing values.
Asked in:
Inmobi,
Accolite,
Adobe,
Amazon,
DE Shaw,
Flipkart,
Goldman Sachs,
InfoEdge,
MakeMyTrip,
Microsoft,
Oracle
Please write comments if you find any of the above codes/algorithms incorrect, or find better ways to solve the same problem.
Share your thoughts in the comments
Please Login to comment...