Z test in R

Hypothesis testing, also known as significance testing, is a statistical test that is used to conclude the population based on assumption. Here two hypotheses are proposed. One is the null hypothesis, and the other is the alternate hypothesis. For hypothesis testing different tests are used. The tests have been categorized in two ways:

• Parametric Test: These tests make assumptions about the population parameters. Some of the tests are Z Test, F test etc.
• Non-Parametric Tests: These tests do not make any assumptions about the population parameters.

What is Z Test?

Z test is a popular parametric test used for hypothesis testing. Z test is a statistical method used to determine if there is a significant difference between sample and population means or between the means of two samples. It is used when there is a large sample size and the population. It is to be noted that Z Test follows normal distribution. The Z value acts as a threshold. Based on its value it is decided whether to accept the hypothesis or reject the hypothesis. This test is applicable where the sample size is greater than 30.

There are two types of Z tests based on samples:

• One Sample Z-test
• Two Sample Z-test

One Sample Z test

Here Z Test is applicable on one sample that has been taken from the population. The formula is as follows:

Here,

• Z denotes the Z value
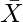• is the sample mean
• denotes mean of the population
• denotes population standard deviation
• n denotes sample size.

Two sample Z test

Here Z Test is applicable on two samples that has been taken from the population. The formula is as follows:

Here,

• are the sample means.
• s1 and s2 are standard deviations of the two samples.
• n1 and n2 are sample sizes of two samples.

Application of Z-test

Z-test is applied when:

1. Population Standard Deviation is Known:
   • We use z-test when, we know the standard deviation of the population and are comparing a sample mean to a population mean or comparing means of two independent samples.
   • If you know the average height of a population and you want to test whether a sample of individuals has a significantly different average height.
2. Large Sample Size:
   • The Z-test is most reliable when dealing with large sample sizes (typically, n > 30 is considered “large”).
   • As the sample size increases, the sampling distribution of the sample mean becomes approximately normal, according to the Central Limit Theorem. Therefore, the Z-test becomes more appropriate as the sample size increases.

Z test in R

R is a popular high level programming language used for statistical analysis. It is open-source programming language as it has a huge community and users can contribute to the development as well. It has vast number of packages which allows the data miners to perform statistical analysis and data visualizations in an interactive manner.

The syntax of z- test in R is:

z.test(x, y, alternative='two.sided', mu=0, sigma.x=NULL, sigma.y=NULL,conf.level=.95)

Now we can conduct one sample test and two sample tests in R.

Here we provide the vector(s) and also provide the value of standard deviation and population mean whose hypothesis is to be tested against. Then we use z.test to calculate the z value. This method provides a complete summary of the output.

The one sample test is as follows:

Here,

• mu is the population mean under the null hypothesis.
• sigma.x is the known population standard deviation.

R

library(BSDA)

# Sample data
sample_data <- c(26, 25, 10, 34, 30, 23, 28, 29, 25, 27)

# One-sample Z-test
z_test <- z.test(sample_data, mu = 24,sigma.x=10)

# Print the result
print(z_test)

Output:

    One-sample z-Test
data:  sample_data
z = 0.53759, p-value = 0.5909
alternative hypothesis: true mean is not equal to 24
95 percent confidence interval:
 19.50205 31.89795
sample estimates:
mean of x 
     25.7 

The z.test function returns a test result object that includes the test statistic, p-value, and other relevant information.

The output of the z test is:

• Test Statistics (z): 0.53759
• P-value: 0.5909
• Alternative Hypothesis: The true mean is not equal to 24.
• 95% Confidence Interval: The confidence interval for the true mean is given as (19.50205, 31.89795).
• Sample Estimate (mean of x): 25.7

The p-value is 0.5909 and the value is greater than the chosen significance level, hence, we will fail to reject the null hypothesis. There is not enough evidence to suggest that the true mean is different from 24 based on your sample data. The 95% confidence interval provides a range of plausible values for the true mean.

Based on the above output it is said that there is not much evidence to reject null hypothesis. So, the null hypothesis is accepted, and the alternate hypothesis is rejected.

Now we will perform two sample Z-Test

R

# Two vectors of sample data
data1 <- c(27, 24, 18, 29, 30,27)
data2 <- c(23, 28, 20, 19, 35,23)

# Two-sample Z-test
z_test_result <- z.test(data1,data2,mu=26,sigma.x=10,sigma.y=15)

# Print the result
print(z_test_result)

Output:

    Two-sample z-Test
data:  data1 and data2
z = -3.3742, p-value = 0.0007403
alternative hypothesis: true difference in means is not equal to 26
95 percent confidence interval:
 -13.25828  15.59161
sample estimates:
mean of x mean of y 
 25.83333  24.66667 

The output of the two-sample z-test comparing two independent samples:

• Test Statistic (z): -3.3742
• P-value: 0.0007403
• Alternative Hypothesis: The true difference in means is not equal to 26.
• 95% Confidence Interval: (-13.25828, 15.59161)
• Sample Estimates:
  • Mean of Group 1 (data1): 25.83333
  • Mean of Group 2 (data2): 24.66667

From the above output we can see that the z-value is negative, and the p value is very small. So based on the above calculations we can say that there is sufficient evidence to accept null hypothesis. In this case we have to accept alternate hypothesis.